Points X and Y are taken on the sides QR and RS, respectively of a parallelogram PQRS, so that QX=4XR and RY=4YS. The line XY cuts the line PR at Z. Then, PZ is
2125PR
1625PR
1725PR
none of these
The correct Answer is:A
4(5a+4b3)+a+5b54+1=21(a+b)25=2125PR

PV of X is 4(a+b)+a5=5a+4b5
PV of Y is 4b+a+b5=a+5b5
Now, PZ=mPR
PZ=m(a+b)
Let Z divided YX in the ratio λ:1
PV of Z=λOX+OYλ+1
∴PZ=(5a+4b5)+a+5b5λ+1=m(a+b)
Comparing coefficients of a and b
m=5λ+15(λ+1)
and m=4λ+55(λ+1)
∴λ=4
∴PZ=4(5a+4b5)+a+5b54+1
=21(a+b)25=2125PR.
Topper's Solved these Questions
- BOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise (More Than One Correct Option Type Questions)7videos
VECTOR ALGEBRA
- BOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise (Statement I And Ii Type Questions)3videos
VECTOR ALGEBRA
- BOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise For Session 311videos
VECTOR ALGEBRA
- BOOK - ARIHANT MATHSCHAPTER - TRIGONOMETRIC FUNCTIONS AND IDENTITIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)19videos
TRIGONOMETRIC FUNCTIONS AND IDENTITIES
Similar Questions
Points X and Y are taken on the sides QR and RS, respectively of a parallelogram PQRS, so that QX=4XR and RY=4YS The line XY cuts the line PR at Z Find the ratio PZ: ZR
View SolutionS and T are points on the sides PQ and PR, respectively of ΔPQR, such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of ΔPST and ΔPQR.
View Solution
Knowledge Check
- Question 1 - Select One
The diagonals of a parallelogram PQRS are along the lines x+3y=4 and 6x-2y=7. Then PQRS must be a
ARectangleBSquareCCyclic QuadrilateralDRhombus - Question 2 - Select One
The diagonals of parallelogram PQRS are along the lines x+3y=4 and 6x−2y=7. Then PQRS must be a
ArectangleBsquareCcyclic quadrilateralDrhombus - Question 3 - Select One
In ΔPQR,right-angled at Q,X,Y and Z are points on sides PR,RQandPQrespectively such that QX⊥PR,XY⊥RQandXZ⊥PQ . Find the value of XZ If PZ=4cmandZQ=9cm.
A5 cm.B6 cm.C8 cm.D9 cm.
In the adjoining figure, S and T are points on the sides PQ and PR respectively of ΔPQR such that PT=2cm,TR=4cmandST is parallel to QR. Find the ratio of the ares ofΔPSTandΔPQR.
 View Solution
View SolutionIn the given figure L, M and N are mid point of the sides PQ, PR and QR respectively of ΔPQR. If PQ = 4.4 cm, QR = 5.6 cm and PR = 4.8 cm then find the perimeter of ΔLMN.
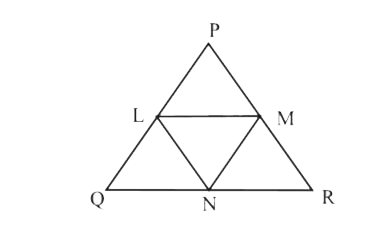 View Solution
View SolutionThe diagonals of a parallelogram PQRS are along the lines x+3y =4 and 6x-2y = 7, Then PQRS must be :
View Solutionthe diagonals of the parallelogram PQRS are along the lines x+3y=4 and 6x−2y=7 then PQRS is must be:
View SolutionA circle passing through points Q and R of triangle PQR, cut the sides PQ and PR at point X and Y respectively. If PQ = PR, then what is the value (in degrees) of ∠PRQ+∠QXY ?
View Solution

