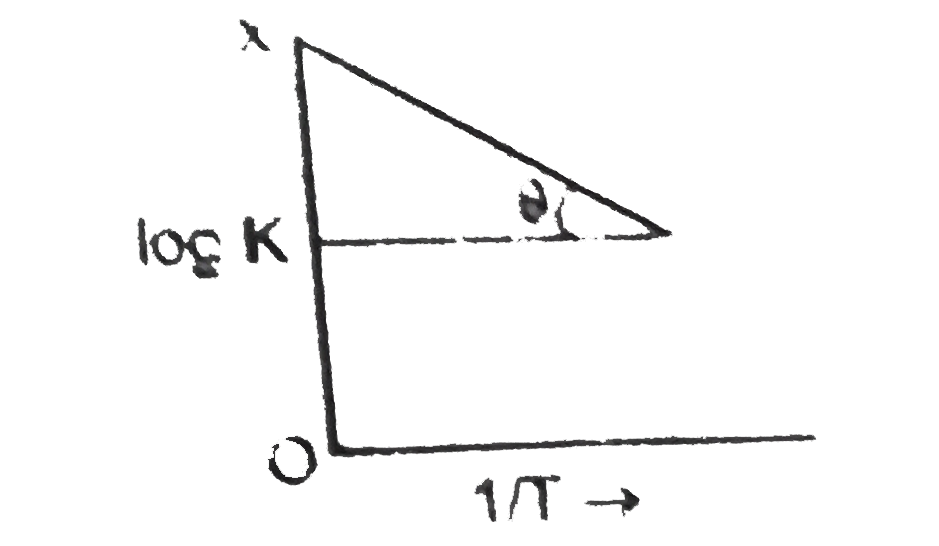
Graph between $log k$ and $1 / T$ [ $k$ rate constant $(s^{- 1})$ and $T$ and the temperature $(K)$ ] is a straight line with $O X = 5, θ = {tan}^{- 1} (1 / 2.303)$ . Hence $- E_{a}$ will be

A

$2.303 \times 2 c a l$

B

$2 / 2.303 c a l$

C

$2 c a l$

D

None

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

$log k = log A - \frac{E_{a}}{2.303 R T} (y = c + m x)$
Slope $= \frac{- E_{a}}{2.303 R} = \frac{1}{2.303} (g i v e n) (tan θ = \frac{1}{2.303})$
$- E_{a} = 2.303 R \times s l o p e$
$= 2.303 \times \frac{R}{2.303} = R = 2 c a l$

Updated on:21/07/2023

|

Class 12 CHEMISTRY CHEMICAL KINETICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Graph between $log k$ and $1 / T$ [ $k$ rate constant $(s^{- 1})$ and $T$ and the temperature $(K)$ ] is a straight line with $O X = 5, θ = {tan}^{- 1} (1 / 2.303)$ . Hence $- E_{a}$ will be

A $2.303 \times 2$ cal
B $2 / 2.303$ cal
C2 cal
Dnone
Graph between log k and $1 / T$ [where K is rate constant in $s^{- 1}$ and T is the temperature (in K) is a straight line with Hence, $E_{a}$ will be

A $2.303 \times 2$ cal
B $\frac{2}{2.303} c a l$
C2 cal
DNone of these
Graph between log k and $\frac{1}{T}$ (k is rate constant in $s^{- 1}$ and T is the temperature in K) is a straight line. As shown in figure if OX = 5 and slope of the line $= - \frac{1}{2.303}$ then $E_{a}$ is :

A $2.303 \times 2 c a l$
B $\frac{2}{2.303} c a l$
C2 cal
Dnone of these

CENGAGE CHEMISTRY-CHEMICAL KINETICS-Exercises Single Correct

Home
Ask Doubt
Profile