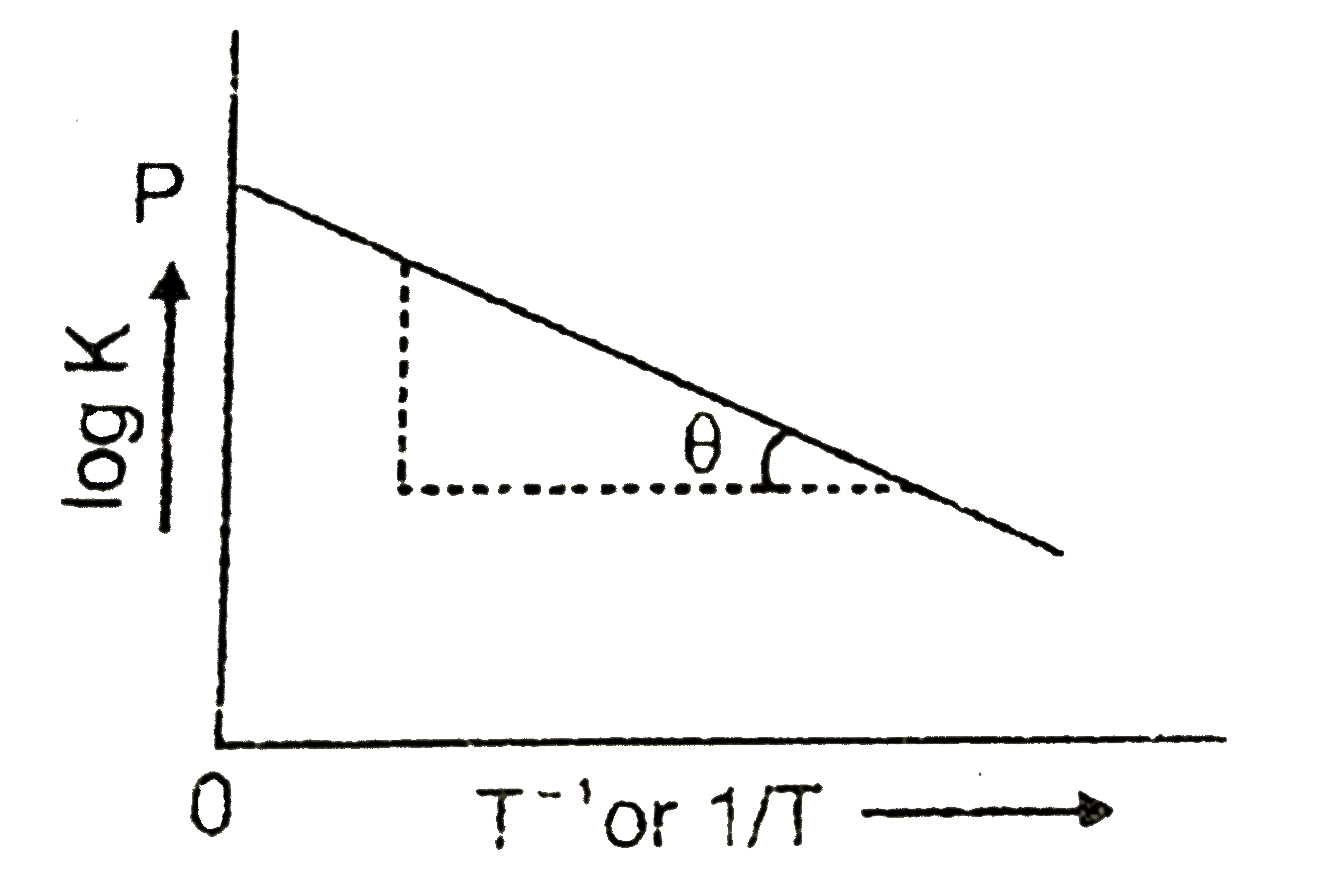
The graph between log k and 1/T[K is rate constant ( ${sec}^{- 1}$ ) and T the temperature (K)] is a straight line with $O X = 5 and θ = {tan}^{- 1} (- \frac{1}{2.303})$ .Calculate the value of $E_{a}$ is cal. ?

Text Solution

Verified by Experts

The correct Answer is:2

$2.303 log K = - \frac{E_{a}}{R T} + 2.303 log Å$
Thus, $- \frac{E_{a}}{2.303 R} = tan θ = - \frac{1}{2.303}$
$∴ E_{a} = R = 2$ cal.

|

Updated on:21/07/2023

Class 12 CHEMISTRY QUESTION BANK

Topper's Solved these Questions

BOOK - RESONANCECHAPTER - QUALITATIVE ANALYSIS PART 1EXERCISE - A.L.P
39videos
QUALITATIVE ANALYSIS PART 1
BOOK - RESONANCECHAPTER - SOLID STATEEXERCISE - PHYSICAL CHEMITRY (SOLID STATE)
45videos
SOLID STATE

Similar Questions

Knowledge Check

Question 1 - Select One
Graph between $log k$ and $1 / T$ [ $k$ rate constant $(s^{- 1})$ and $T$ and the temperature $(K)$ ] is a straight line with $O X = 5, θ = {tan}^{- 1} (1 / 2.303)$ . Hence $- E_{a}$ will be

A $2.303 \times 2 c a l$
B $2 / 2.303 c a l$
C $2 c a l$
DNone
Question 2 - Select One
Graph between $log k$ and $1 / T$ [ $k$ rate constant $(s^{- 1})$ and $T$ and the temperature $(K)$ ] is a straight line with $O X = 5, θ = {tan}^{- 1} (1 / 2.303)$ . Hence $- E_{a}$ will be

A $2.303 \times 2$ cal
B $2 / 2.303$ cal
C2 cal
Dnone
Question 3 - Select One
Graph between log k and $1 / T$ [where K is rate constant in $s^{- 1}$ and T is the temperature (in K) is a straight line with Hence, $E_{a}$ will be

A $2.303 \times 2$ cal
B $\frac{2}{2.303} c a l$
C2 cal
DNone of these

RESONANCE-RANK BOOSTER-All Questions

Home
Ask Doubt
Profile