14 सेमी त्रिज्या वाले एक वृत्त का एक चतुर्थांश PQRA है अर्द्ध - वृत्त का व्यास PR द्वारा दर्शाया गया है तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए ।
यहाँ, समकोण ΔPQR में,
PR2=PQ2+QR2=(14)2+(14)2
⇒ PR=√2×(14)2=14√2 सेमी
⇒ PR2=14√22सेमी =7√2सेमी
अब छायांकित भाग (A) का क्षेत्रफल = PARBP का क्षेत्रफल
= PRBP का क्षेत्रफल - PRAP का क्षेत्रफल
= PRBP का क्षेत्रफल -(PQRAP का क्षेत्रफल −ΔPQR का क्षेत्रफल)
=(अर्द्धवृत्त का RP व्यास के साथ क्षेत्रफल)-(त्रिज्या AB के साथ एक वृत्त के एक चतुर्थांश का क्षेत्रफल −ΔPQR का क्षेत्रफल)
=[12(227×(7√2)2)]−[14×227×(14)2−14×14×14]सेमी2
=[12×227×49×2−14×227×14×14+12×14×14] सेमी2
=(154−154+98) सेमी2
98 सेमी2

Topper's Solved these Questions
- वृत्तों से समबन्धित क्षेत्रफल BOOK - BALAJI PUBLICATIONCHAPTER - वृत्तों से समबन्धित क्षेत्रफल EXERCISE - अभ्यास प्रश्न 12.1
10 Videos
- वृत्तों से समबन्धित क्षेत्रफल BOOK - BALAJI PUBLICATIONCHAPTER - वृत्तों से समबन्धित क्षेत्रफल EXERCISE - अभ्यास प्रश्न 12.2
10 Videos
- वृत्त BOOK - BALAJI PUBLICATIONCHAPTER - वृत्त EXERCISE - स्वमूल्यांकन परीक्षण
15 Videos
- समांतर श्रेणीBOOK - BALAJI PUBLICATIONCHAPTER - समांतर श्रेणीEXERCISE - स्वमूल्यांकन परीक्षण
22 Videos
Similar Questions
एक वृत्त की त्रिज्या 8.4 सेमी है वृत्त की परिधि तथा क्षेत्रफल ज्ञात कीजिए
View Solution21 सेमी त्रिज्या वाले एक वृत्त से एक त्रिज्यखण्ड काटा जाता है त्रिज्यखण्ड का कोण 150∘ है चाप की लम्बाई तथा क्षेत्रफल ज्ञात कीजिए ।
View Solutionदिये गये चित्र में TAB, O केंद्र वाले वृत्त की छेदक रेखा है तथा वृत्त के बिन्दु P पर TP एक स्पर्शी है। यदि TP = 5.6 सेमी तथा TA = 2.8 सेमी हो तब जीवा AB की माप ज्ञात कीजिए ।
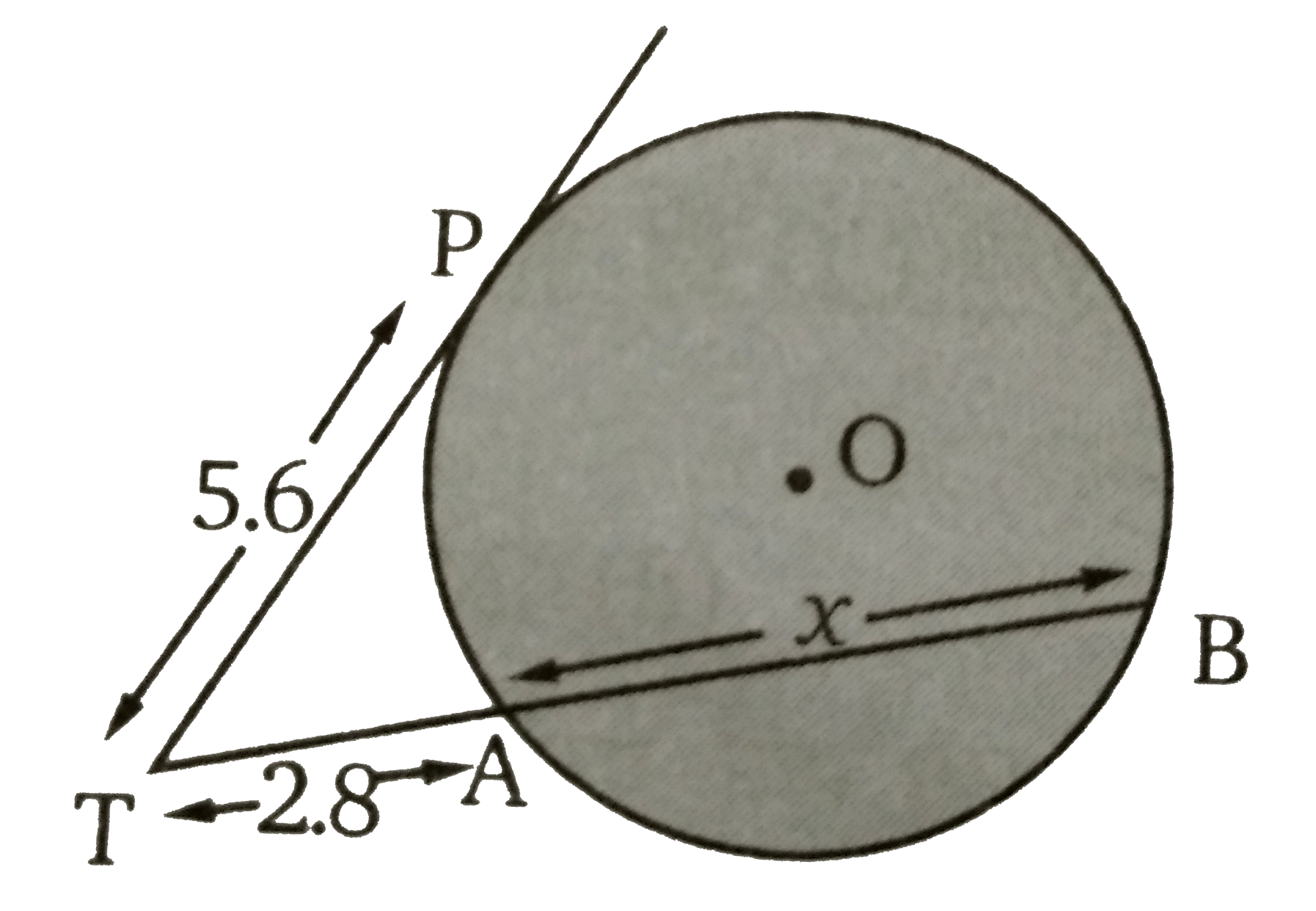
View Solutionसिद्ध कीजिए कि निम्न स्थिति एक समांतरर श्रेणी बनाती है। एक दीवार को पहले एक मीटर बनाने का खर्च रू0 150 तथा प्रत्येक आनेवाले मीटर में रू0 20 का खर्च बढ़ता है।
View Solution8.8cm लम्बा एक रेखाखण्ड AB खींचिए। A को केंद्र मानकर 4 त्रिज्या का एक वृत्त तथा 3 को केंद्र लेकर त्रिज्या का एक अन्य वृत्त खींचिए। प्रत्येक वृत्त पर दूसरे वृत्त के केंद्र से स्पर्श रतेखाओ कि रचना कीजिए।
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionकिसी वृत्त में एक चाप केन्द्र पर 45∘का कोण बनाता है। यदि चाप की लम्बाई 11 सेमी है तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionएक वृत्त का केंद्र (2x−1,3x+1) है। x ज्ञात कीजिए यदि वृत्त (-3,-1) में से गुजरे और व्यास की लम्बाई 20 मात्रक हो।
View Solution10 सेमी. व्यास वाले अर्धगोले का सम्पूर्ण पृष्ट को क्षेत्रफल ज्ञात कीजिए|
View Solutionएक बेलन का व्यास 10 सेमी. तथा ऊंचाई 7 सेमी. है, तो बेलन का आयतन ज्ञात कीजिए।
View Solutionयदि किसी वृत्त के व्यास का एक सिरा (3,4) और केन्द्र (2,3) हो, तो दूसरे सिरे के निर्देशांक ज्ञात कीजिए।
View Solutionयदि किसी वृत्त के व्यास का एक सिरा (3, 4) और केन्द्र (2,3) हो, तो दूसरे सिरे का निर्देशांक ज्ञात कीजिए।
View Solutionयदि किसी वृत्त के व्यास का एक सिरा (3, 4) और केन्द्र (2,3) हो, तो दूसरे सिरे का निर्देशांक ज्ञात कीजिए।
View SolutionIn the given figure, PQR is a quadrant whose radius is 7cm.A circle is incribed in the quadrant as shown in the figure.What is the area (in cm2) of the circle?
दी गई आकृति में, PQR एक वृत्त-खण्ड है जिसकी त्रिज्या 7 से.मी. है। जेसा कि आकृति में दर्शाया गया है कि वृत्त-खण्ड में एक वृत्त को अंकित किया गया हें वृत्त का क्षेत्रफल (से.मी.2 में) क्या है?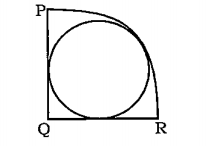
View SolutionA is the centre of circle whose radius is 8 units and B is the centre of a circle whose diameter is 8 units. If these two circles touch externally, then the area of the circle with radius AB is - A,8 इकाई त्रिज्या वाले वृत्त का केन्द्र है और B, 8 इकाई व्यास वाले वृत्त का केन्द्र है ।यदि ये दोनों वृत्त बाहर से स्पर्श करते हैं, तो AB त्रिज्या वाले वृत्त का क्षेत्रफल कितना है ?
View Solution7 cm त्रिज्या वाले वृत्त का अर्द्धपरिमाप ज्ञात करो -
View Solution
