दिखाए गए वेक्टरो −−→OA,−−→OB तथा −−→OC के परिमाण बराबर है। वेक्टर −−→OA+−−→OB−−−→OC की दिशा बताएँ।
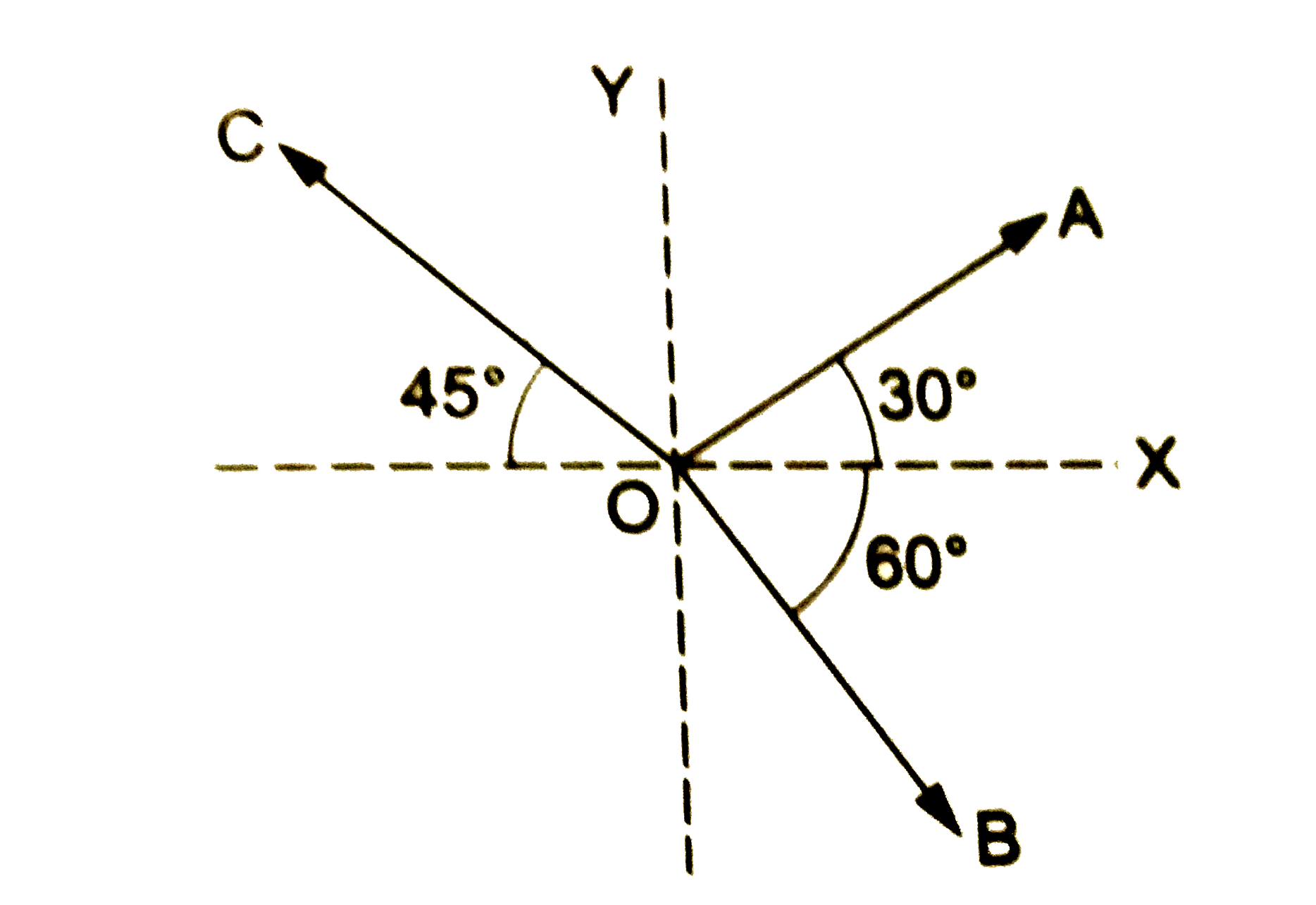
मान ले कि OA=OB=OC=F.
−−→OA=(OAcos30∘)ˆi+(OAsin30∘)ˆj=F(√32ˆi+12ˆj).
−−→OB=(OBcos60∘)ˆi−(OBsin60∘)ˆj=F(12ˆi−√32j).
−−→OC=−(OCcos45∘)ˆi+(OCsin45∘)ˆj=F(−1√2i+1√2ˆj).
अतः −−→OA+−−→OB−−−→OC=F[(√32+12−1√2)ˆi+(12−√32−1√2)ˆj]
यदि यह वेक्टर x -अक्ष से α कोण बनाए, तो
tanα=y−घटकx−घटक=12−√32−12√32+12+1√2=1−√3−√21+√3+√2.
अतः α=tan−11−√3−√21+√3+√2.
Topper's Solved these Questions
- सदिश राशियों का गणित BOOK - HC VERMA HINDICHAPTER - सदिश राशियों का गणित EXERCISE - अभ्यास
15 Videos
- सदिश राशियों का गणित BOOK - HC VERMA HINDICHAPTER - सदिश राशियों का गणित EXERCISE - विचार हेतु प्रश्न
16 Videos
- संवेग- संरक्षण का सिद्धांत, टक्कर BOOK - HC VERMA HINDICHAPTER - संवेग- संरक्षण का सिद्धांत, टक्कर EXERCISE - अभ्यास के प्रश्न
57 Videos
- समतल में गति BOOK - HC VERMA HINDICHAPTER - समतल में गति EXERCISE - अभ्यास के प्रश्न
21 Videos
Similar Questions
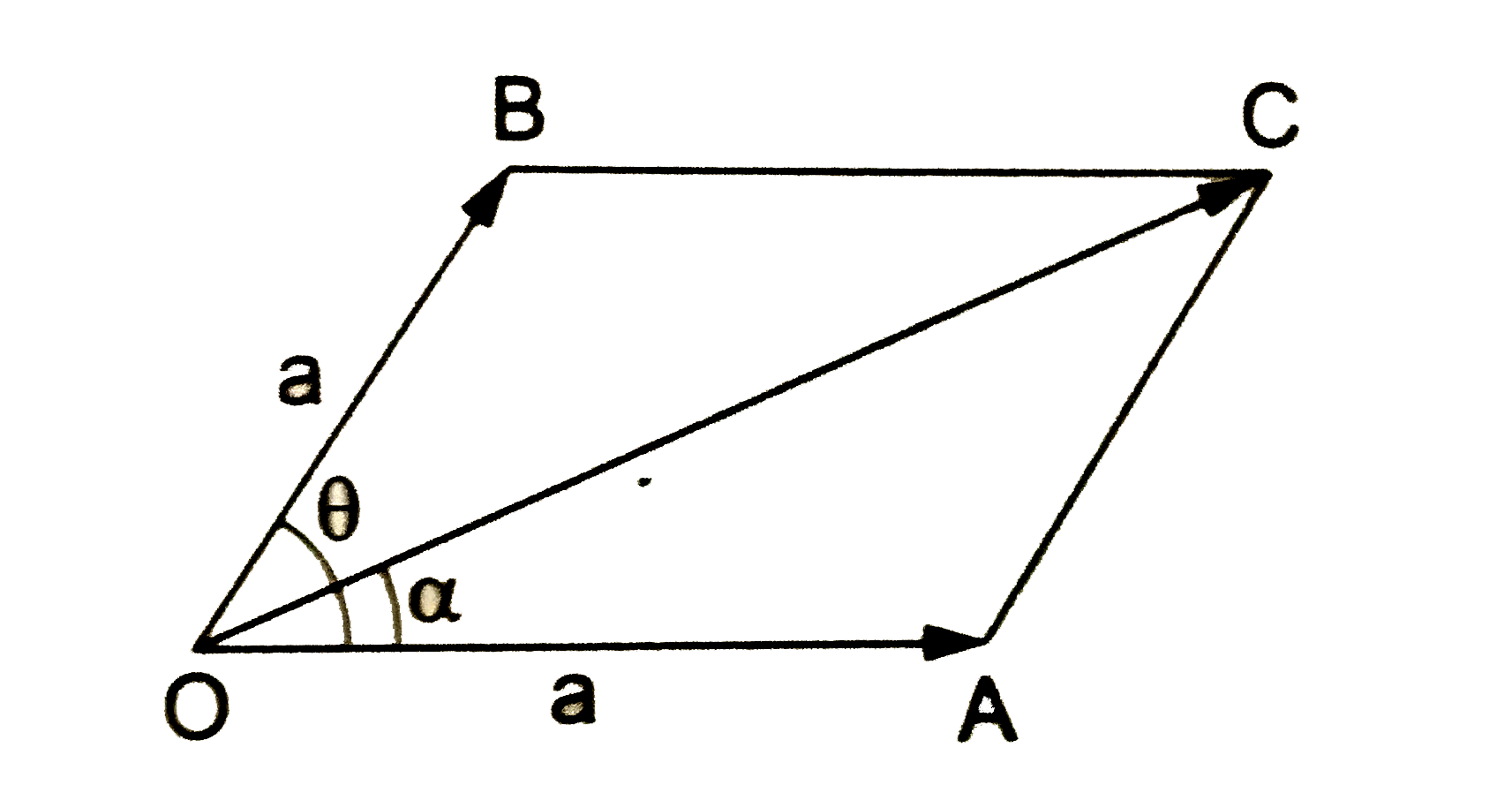
समान लंबाई के दो वेक्टर −−→OA तथा −−→OB आपस में θ कोण बनाते है. सिद्ध करे कि उनका परिणामी वेक्टर इस कोण को समद्विभाग करेगा.
View Solutionयदि एक वेक्टर को अपने एक सिरे के परित: किसी कोण से घुमा दिया जाए, तो क्या वह वेक्टर अवश्य ही बदल जाएगा?
View Solution1.0 kg तथा 4.0kg द्रव्यमानों के दो कणों की गतिज ऊर्जाएँ बराबर हैं। इनके रैखिक संवेगों का अनुपात ज्ञात कीजिए।
View Solutionएक मनुष्य को एक पार्क में जाने के लिए अपने घर से 50 m उत्तर , फिर 40 m पूर्व ओर फिर 20 m दक्षिण जाना पड़ता है । (a ) उसे अपने घर से पार्क तक पहुँचने में कितनी दुरी चलनी पड़ती है ? (b ) घर से पार्क तक के विस्थापन का परिमाण बताएं ।
View SolutionLet O be the centre of a regular hexagon ABCDEF . Find the sum of the vectors →OA,→OB,→OC,→OD,→OEand→OF .
View SolutionGiven a regular hexagon ABCDEF with centre o,show that vec OB-vec OA=vec OC-vec OD
View SolutionThe magnitudes of vectors vec OA,vec OB and vec OC( in figure( 2-W3) are equal.Find the direction of )/(Ovec A)+vec OB-vec OC.
View SolutionLet O be the centre of the regular hexagon ABCDEF then find −−→OA+−−→OB+−−→OD+−−→OC+−−→OE+−−→OF
View SolutionThe magnitude of vectors −−→OA,−−→OBand−−→OC in figure are equal. Find the direction of −−→OA+−−→OB−−−→OC.
 .
.
View Solutionमाना कि O समष्टभुज ABCDEF का केंद्र हैं, तो
−−→OA+−−→OB+−−→OC=−−→OD+−−→OE+−−→OF.
View SolutionIf OAB is a tetrahedron with edges and ˆp,ˆq,ˆr are unit vectors along bisectors of
−−→OA,−−→OB:−−→OB,−−→OC:−−→OC,−−→OA respectively and ˆa=−−→OA∣∣∣−−→OA∣∣∣,→b=−−→OB∣∣∣−−→OB∣∣∣,→c=−−→OC∣∣∣−−→OC∣∣∣, then :
View SolutionIf OAB is a tetrahedron with edges and ˆp,ˆq,ˆr are unit vectors along bisectors of
−−→OA,−−→OB:−−→OB,−−→OC:−−→OC,−−→OA respectively and ˆa=−−→OA∣∣∣−−→OA∣∣∣,→b=−−→OB∣∣∣−−→OB∣∣∣,→c=−−→OC∣∣∣−−→OC∣∣∣, then :
View SolutionABCDEF is a regular hexagon. Show that :
−−→OA+−−→OB+−−→OC+−−→OD+−−→OE+−−→OF=→0
View SolutionThe magnitude of vectors −−→OA,−−→OBand−−→OC in figure are equal. Find the direction of −−→OA+−−→OB−−−→OC.
 .
.
View SolutionProve that 3−−→OD+−−→DA+−−→DB+−−→DC is equal to −−→OA+−−→OB+−−→OC.
View Solution
