If OAB is a tetrahedron with edges and $ˆ p, ˆ q, ˆ r$ are unit vectors along bisectors of
$- - \to O A, - - \to O B : - - \to O B, - - \to O C : - - \to O C, - - \to O A$ respectively and $ˆ a = \frac{- - \to O A}{∣ ∣ ∣ - - \to O A ∣ ∣ ∣}, \to b = \frac{- - \to O B}{∣ ∣ ∣ - - \to O B ∣ ∣ ∣}, \to c = \frac{- - \to O C}{∣ ∣ ∣ - - \to O C ∣ ∣ ∣}$ , then :

$\frac{[ˆ a ˆ b ˆ c]}{[ˆ p ˆ q ˆ r]} = \frac{3 \sqrt{3}}{2}$

$\frac{[ˆ a + ˆ b ˆ b + ˆ c ˆ c + ˆ a]}{[ˆ p + ˆ q ˆ q + ˆ r ˆ r + ˆ p]} = \frac{3 \sqrt{3}}{4}$

$\frac{[ˆ a + ˆ b ˆ b + ˆ c ˆ c + ˆ a]}{[ˆ p ˆ q ˆ r]} = \frac{3 \sqrt{3}}{2}$

$\frac{[ˆ a ˆ b ˆ c]}{[ˆ p + ˆ q ˆ q + ˆ r ˆ r + ˆ p]} = \frac{3 \sqrt{3}}{4}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, D

Answer

Step by step video, text & image solution for If OAB is a tetrahedron with edges and hatp, hatq, hatr are unit vectors along bisectors of vec(OA), vec(OB):vec(OB), vec(OC):vec(OC), vec(OA) respectively and hata=(vec(OA))/(|vec(OA)|), vecb=(vec(OB))/(|vec(OB)|), vec c= (vec(OC))/(|vec(OC)|), then : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS VECTOR ALGEBRA

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
Orthocenter of an equilateral triangle ABC is the origin O. If $- - \to O A = \to a, - - \to O B = \to b, - - \to O C = \to c$ , then $- - \to A B + 2 - - \to B C + 3 - - \to C A =$
A $3 \to c$
B $3 \to a$
C $\to 0$
D $3 \to b$
Question 2 - Select One
The resultant of the three vectors $- - \to O A, - - \to O B$ and $- - \to O C$ shown in figure is

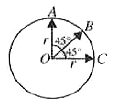Ar
B2r
C $r (1 + \sqrt{s})$
D $r (\sqrt{2} - 1)$
Question 3 - Select One
Let ABCD be a parallelogram whose diagonals intersect at P and let O be the origin. What is $- - \to O A + - - \to O B + - - \to O C + - - \to O D$ equal to
A $2 - - \to O P$
B $4 - - \to O P$
C $6 - - \to O P$
D $8 - - \to O P$

VIKAS GUPTA (BLACK BOOK)-VECTOR & 3DIMENSIONAL GEOMETRY-Exercise-2 : One or More than One Answer is/are Correct

Home
Ask Doubt
Profile

The correct Answer is:A, D

Topper's Solved these Questions

Similar Questions

Knowledge Check

Orthocenter of an equilateral triangle ABC is the origin O. If −−→OA=→a,−−→OB=→b,−−→OC=→c, then −−→AB+2−−→BC+3−−→CA=

The resultant of the three vectors −−→OA,−−→OB and −−→OC shown in figure is

Let ABCD be a parallelogram whose diagonals intersect at P and let O be the origin. What is −−→OA+−−→OB+−−→OC+−−→OD equal to

VIKAS GUPTA (BLACK BOOK)-VECTOR & 3DIMENSIONAL GEOMETRY-Exercise-2 : One or More than One Answer is/are Correct

Orthocenter of an equilateral triangle ABC is the origin O. If $- - \to O A = \to a, - - \to O B = \to b, - - \to O C = \to c$ , then $- - \to A B + 2 - - \to B C + 3 - - \to C A =$

The resultant of the three vectors $- - \to O A, - - \to O B$ and $- - \to O C$ shown in figure is

Let ABCD be a parallelogram whose diagonals intersect at P and let O be the origin. What is $- - \to O A + - - \to O B + - - \to O C + - - \to O D$ equal to