Two co-axisal rings, each of radius R, are separated by a small distance l(ltltR) and carry charges q and -q.Find the electric potential and field at a point on the axis at a distance x from the midpoint between the rings,
The correct Answer is:φ=q/x4πε0(R2+x2)3/2,E=ql(R2−2x2)4πε0(R2+x2)5/2
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENIALBOOK - NN GHOSHCHAPTER - ELECTRIC FIELD AND POTENIALEXERCISE - EXERCISE
21 Videos
- DYNAMO, MOTOR, TRANSFORMERBOOK - NN GHOSHCHAPTER - DYNAMO, MOTOR, TRANSFORMEREXERCISE - EXERCISE
8 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - NN GHOSHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERICISES-B
18 Videos
Similar Questions
Two coaxial rings, eacg of radius R, made of thin wire are separated by a small distabce l(l<<R) and carry the charges q and −q. Find the electric field potential and strength at the axis of the system as a function of the x coordinate (see figure). Investigate these functions at |x|>>R
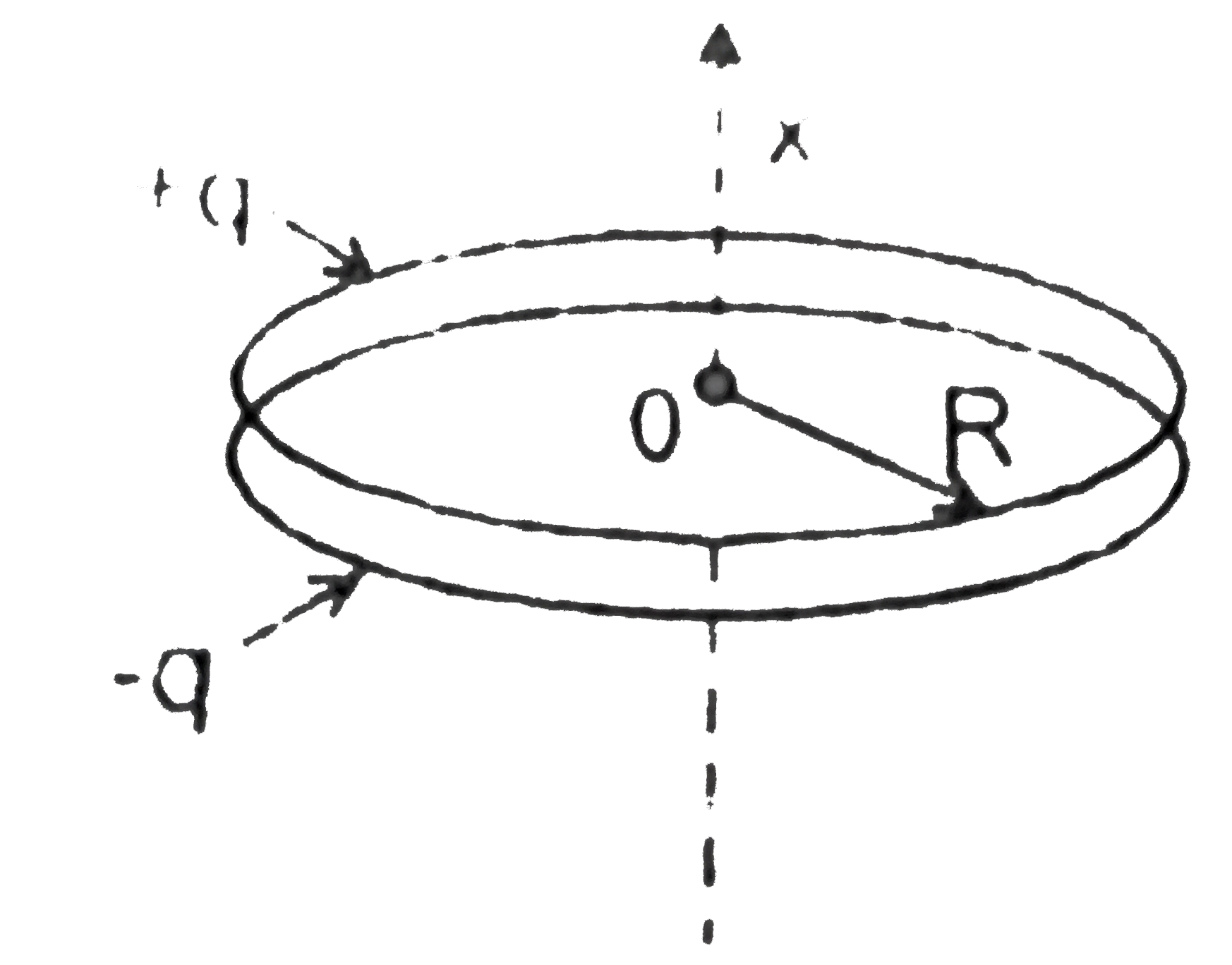
View SolutionTwo coaxial rings, eacg of radius R, made of thin wire are separated by a small distabce l(l<<R) and carry the charges q and −q. Find the electric field potential and strength at the axis of the system as a function of the x coordinate (see figure). Investigate these functions at |x|>>R

View Solution
Knowledge Check
A ring of radius a contains a charge q distributed uniformly over its length. Find the electric field at a point on the axis of the ring at a distance x from the centre.
Akq2x(a2+x2)32B2kq2x(a2+x2)32Ckq2x(a2+x2)32Dkq22x(a2+x2)32A ring of radius R is charged uniformly with a charge +Q. The potential at a point on its axis at a distance 'r' from any point on ring will be-
AkQ√R2+r2BkQrCkQ(r2+R2)3/2DkQr2(r2−R2)1/2
A ring of radius a contains a charge q distributed. uniformly ober its length. Find the electric field at a point. on the axis of the ring at a distance x from the centre.
View SolutionElectric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .

View SolutionElectric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .

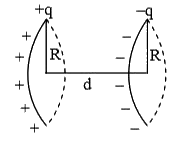
View SolutionTwo thin rings each of radius R are placed at a distance 'd' apart. The charges on the rings are +q and -q. The potential difference between their centres will be -
View SolutionPotential on the axis of ring of radius 3R and at distance 4R from centre of ring is (charge on the ring is Q )
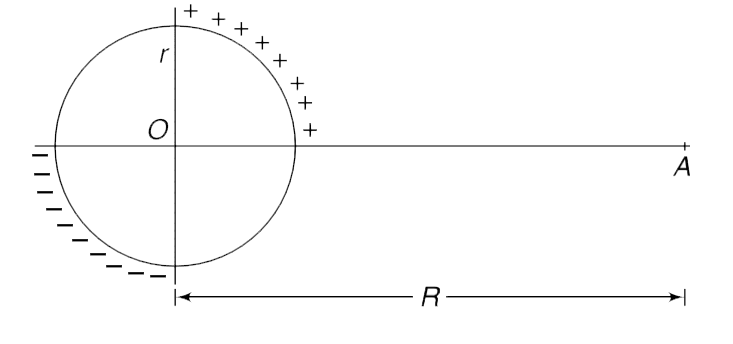
View SolutionA ring of radius r has a uniformly spread charge + q on quarter of its circumference. The opposite quarter of the ring carries a charge – q uniformly spread over it. Find the electric potential at a point A shown in the figure. Point A is at a distance R(gtgt r) from the centre of the ring.
View Solution
