Three masses M1,M2 and M3 are lying on a frictionless table. The masses are connected by massless threads as shown. The mass M3 is pulled by a constant force F as shown. The tension in the thread between masses M2 and M3 is

The correct Answer is:A
For body diagram of masses are
∴F=T1=M3a ………(i)
T1−T2=M2a ….(ii)
T2=M1a …….(iii)
Adding (i) , (ii) , and (iii) we get
F=a(M1+M2+M3)
∴a=F(M1+M2+M3) .......(iv)
T1=(M1+M2)a=(M1+M2)F/M1+M2+M3
Topper's Solved these Questions
Similar Questions
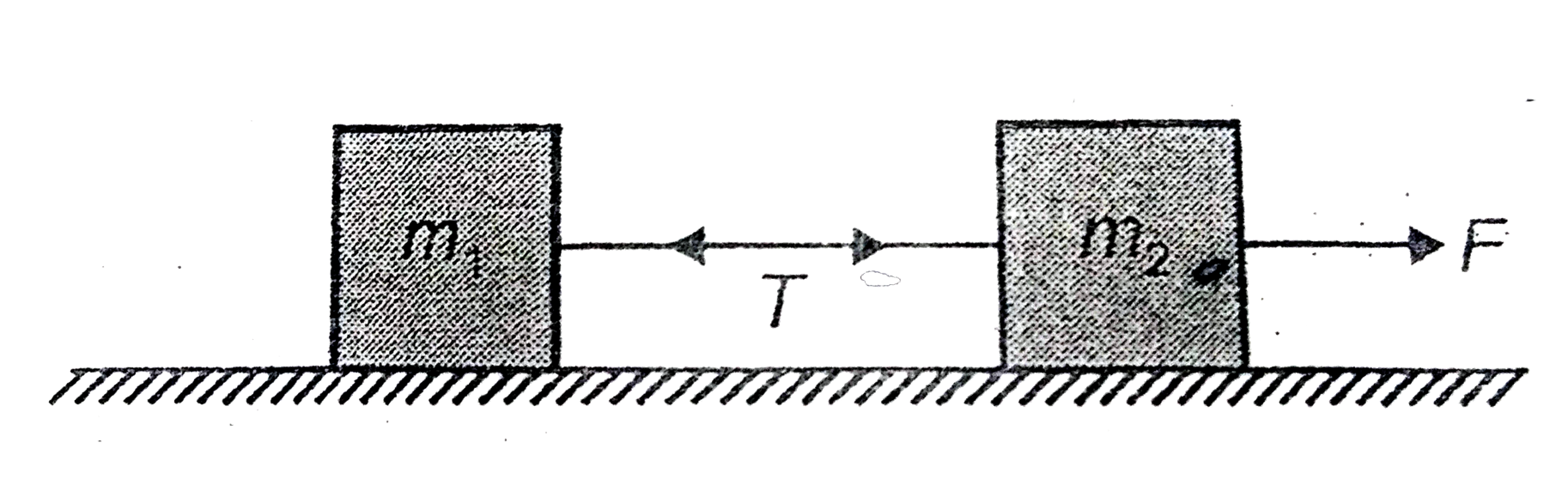
Two block of masses m1andm2 are lying on a frictionless horizontal table connected by a light string m2 is pulled by horizontal force F. Calculate the tension in the string .
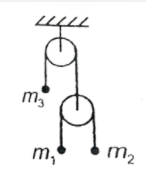
View SolutionThree masses m1,m2andm3 are attached to a string -pulley system as shown . All the three masses are held at rest and then released If m3 remains at rest , then
View Solution
Knowledge Check
Two blocks of mass m1 and m2, resting on a frictionless table, are connected by a stretched spring and then released -
Aratio of speed of blocks is m2/m1Bratio of kinetic energy of blocks is m2/m1Ccentre of mass will move towards heavier blockDmechanical energy will remain conserve in this processTwo masses M and m are connected by a weightless string. They are pulled by a force F on a frictionless horizontal surface. The tension in the string will be
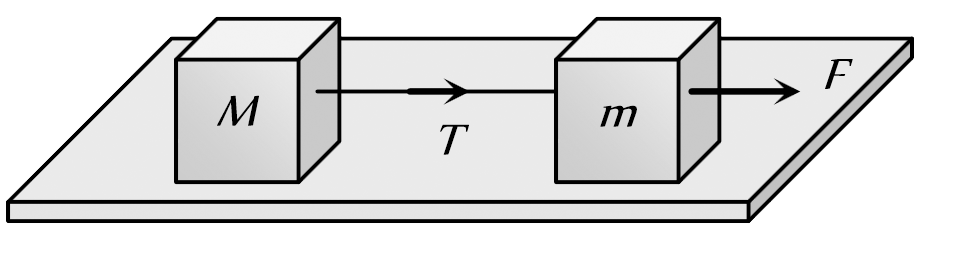 AFMm+MBFM+mCFMmDFmM+m
AFMm+MBFM+mCFMmDFmM+mThree solids of masses m1,m2 and m3 are connected with weightless string in succession and are placed on a frictionless table. If the mass m3 is dragged with a force T , the tension in the string between m2 and m3 is
Am2m1+m2+m3TBm3m1+m2+m3TCm1+m2m1+m2+m3TDm2+m3m1+m2+m3T
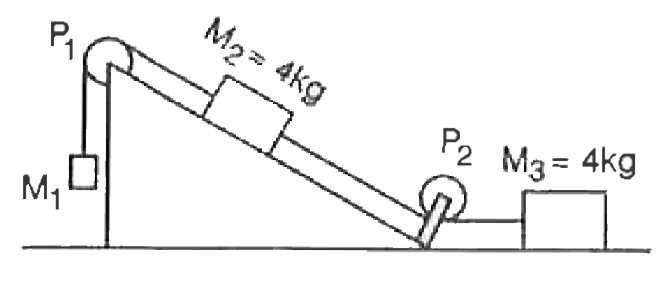
Masses M1,M2andM3 are connected by string of negligible mass which pass over massless and frictionless pulleys P1andP2 as shown in figure 7.15. The masses move such that the string between P1andP2 is parallel to the incline and the portion of the string between P2andM3 is horizontal. The masses M2andM3 are 4.0 kg each and the coefficient of kinetic friction between the masses and the surfces is 0.25. The inclined plane makes an angle of 37∘ with the horizontal. If the mass M1moves downwards with a uniform velocity, find (i) the mass of M1, (ii) the tension in the horizontal portion. (g=9.8ms−2,sin37∘=35)
View SolutionFour blocks each of mass M connected by a massless strings are pulled by a force F on a smooth horizontal surface, as shown in figure.

View SolutionThree point masses m1,m2andm3 are placed at the corners of a thin massless rectangular sheet 1.2m×1m) as shown. Center of mass will be located at the point.
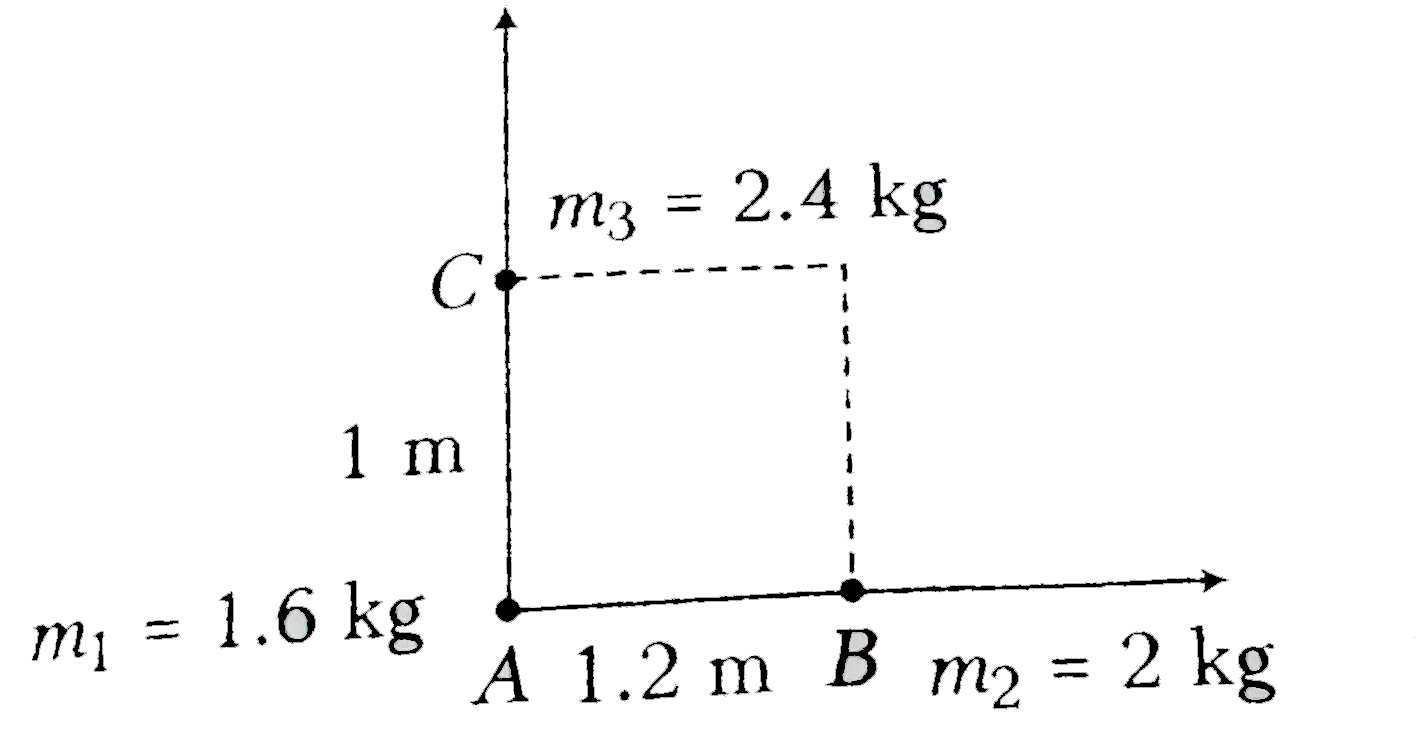
View SolutionTwo blocks of masses m and M are placed on a horizontal frictionless table connected by light spring as shown in the figure. Mass M is pulled to the right with a force F. If the acceleration of mass m is a, then the acceleration of mass M will be

View SolutionTwo blocks of masses m and M are placed on a horizontal frictionless table connected by light spring as shown in figure. The Mass M is pulled to the right with a force F It the acceleration of mass m is a then the acceleration of M will be .

View Solution
