Question

In $\Delta ABC$, $\angle C$ is an acute angle, seg $AD\perp$ seg $BC$. Prove $A{B}^2=B{C}^2+A{C}^2-2BC\times DC$ by completing the following activity.

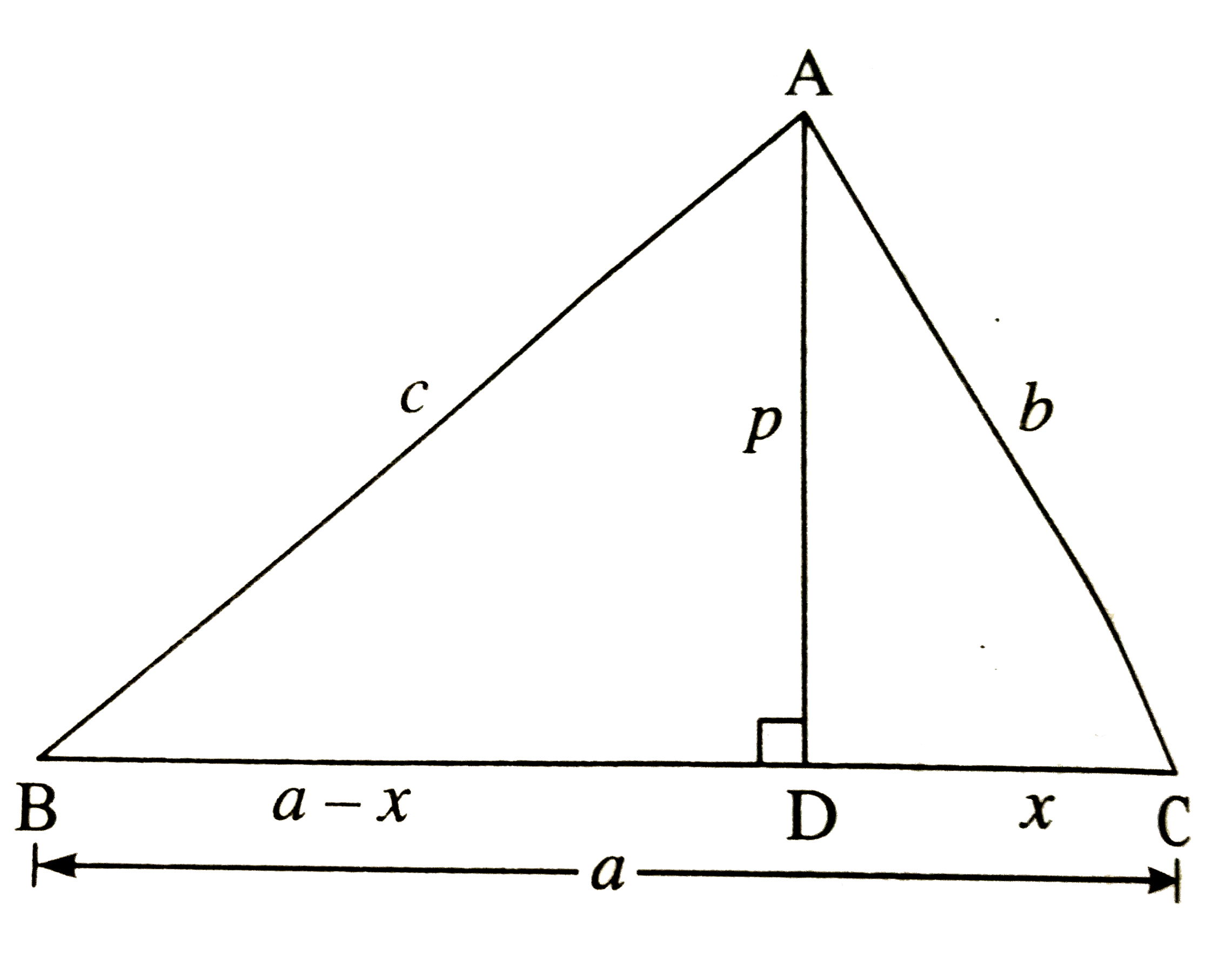
Let $AB=c$, $AC=b$, $AD=p$, $BC=a$, $DC=x$
$\therefore BD=a-x$
In $\Delta ADB$, by Pythagoras theorem,
$c^2={(a-x)}^2+\square$
$c^2=a^2-2ax+x^2+\square$...........$\left(1\right)$
In $\Delta ADC$, by Pythagoras theorem,
$b^2=p^2+\square$
$p^2=b^2-\square$ ..........$\left(2\right)$
Substituting value of $p^2$ from $\left(2\right)$ in $\left(1\right)$
$c^2=a^2-2ax+x^2+\square$
$c^2=a^2+b^2-\square$
$\therefore A{B}^2=B{C}^2+A{C}^2-2BC\times DC$.

Explanation

In `DeltaADB`, by Pythagoras theorem,
`c^(2)=(a-x)^(2)+p^(2)`
`c^(2)=a^(2)-2ax+x^(2)+p^(2)`.......`(1)`
In `DeltaADC`, by Pythagoras theorem,
`b^(2)=p^(2)+x^(2)`
`p^(2)=b^(2)-x^(2)`..........`(2)`
Substituting value of `p^(2)` from `(2)` in `(1)`
`c^(2)=a^(2)-2ax+x^(2)+b^(2)-x^(2)`
`c^(2)=a^(2)+b^(2)-2ax`
`:.AB^(2)=BC^(2)+AC^(2)-2BCxxDC`.