AB एक रेखाखण्ड है तथा P इसका मध्यबिंदु है और AB की समान भुजा पर बिंदु D व E इस प्रकार है कि ∠BAD=∠ABE तथा ∠EPA=∠DPB तो सिद्ध कीजिए कि : ΔDAP≅ΔEBP
यहाँ ∠EPA=∠DPB (दिया है )
⇒∠EPA+∠DPE=∠DPB+∠DPE
⇒∠DPA=∠EPB
ΔEBP तथा ΔDAP में, ∠EPB=∠DPA
BP = AP
तथा ∠EBP=∠DAP
तब सर्वांगसम की ASA कसौटी का प्रयोग करने पर
ΔDAP≅ΔEBP

Topper's Solved these Questions
- त्रिभुजों की सर्वांगसमता BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुजों की सर्वांगसमता EXERCISE - अभ्यास प्रश्न 12.1
11 Videos
- त्रिभुजों की सर्वांगसमता BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुजों की सर्वांगसमता EXERCISE - अभ्यास प्रश्न 12.2
4 Videos
- त्रिभुज एवं उसके गुण BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुज एवं उसके गुण EXERCISE - स्वमूल्यांकन परिक्षण ( Self Assessment Test)
13 Videos
- दो चरो के रैखिक समीकरण BOOK - BALAJI PUBLICATIONCHAPTER - दो चरो के रैखिक समीकरण EXERCISE - स्वमूल्यांकन परीक्षण
18 Videos
Similar Questions
चित्र में वर्ग ABCD में एक बिंदु X है । AX पर एक वर्ग AXYZ बनाया जाता है ।
सिद्ध कीजिए किBX = DZ

View Solutionदिये गये चित्र में यदि ∠X=∠Y तथाAB=CB तब सिद्ध कीजिए कि AE = CD
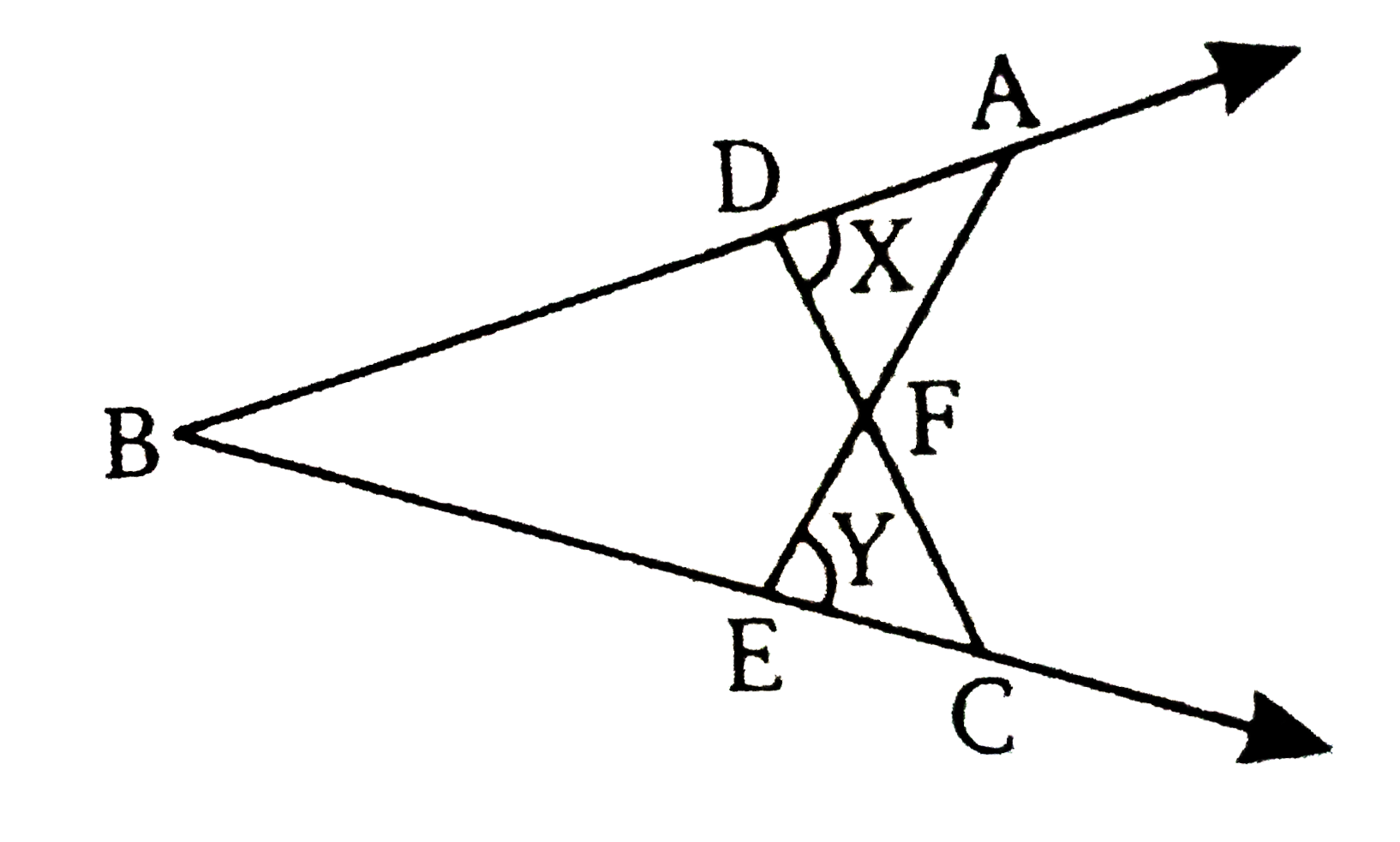
View Solutionयदि एक त्रिभुज का एक कोण, अन्य दो के योग के बराबर है तब सिद्ध कीजिए की त्रिभुज एक समकोण त्रिभुज है।
View Solutionएक पुस्तक का मूल्य, एक पैन के मूल्य से दो गुना है | इसे व्यक्त करने के लिए दो चरो का रैखिक समीकरण लिखिये |
View SolutionAB is a line segment and P is its midpoint. D and E are points on the same side of AD such that ∠BAD=∠ABEand∠EPA=∠DPB.
Show that (i) ΔDAP≅ΔEBP,
(ii)AD=BE.
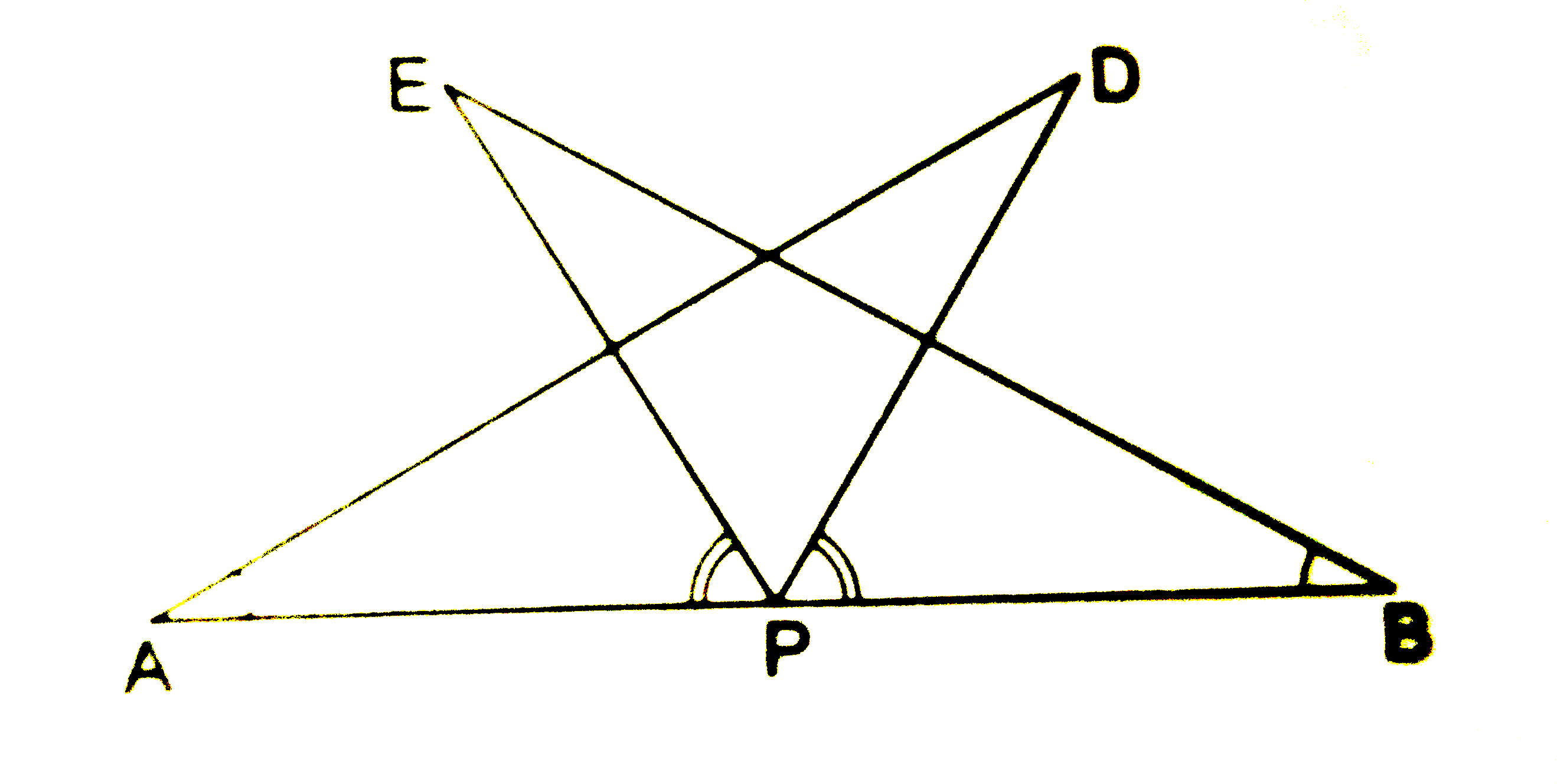
View SolutionAB एक रेखाखंड है और P इसका मध्य बिंदु है | D और E रेखाखंड AB के एक ही ओर स्थित दो बिंदु इस प्रकार हैं कि ∠BAD=∠ABE और ∠EPA=∠DPB है | (देखिए चित्र) | दर्शाइए कि
(i) ΔDAP≅ΔEBP
(ii) AD = BE
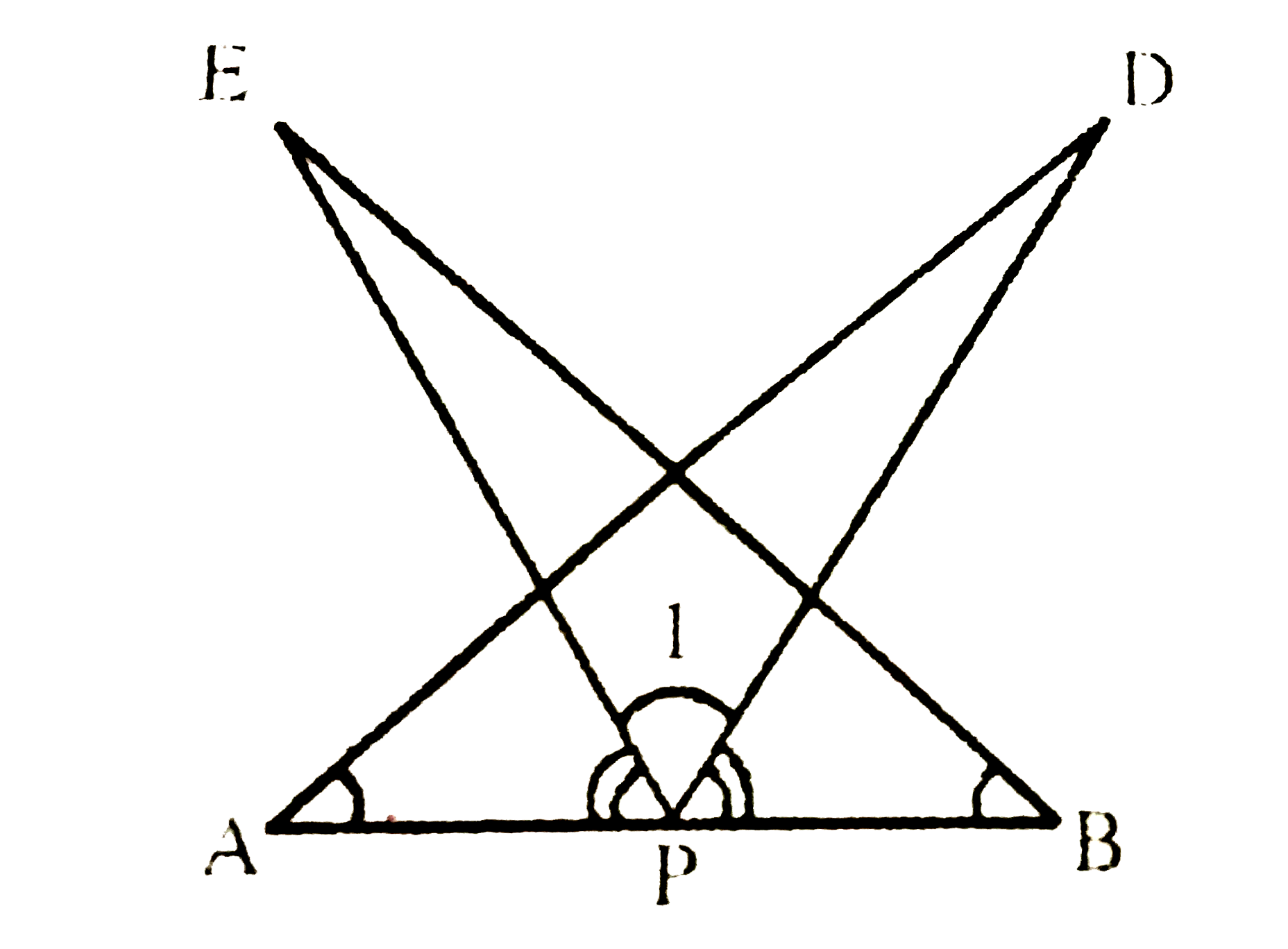
View Solutionरेखाखण्ड AB अक्षो के बीच इस प्रकर गति करता है की A सदैव Y-अक्ष पर तथा B सदैव X- अक्ष पर हो । रेखाखण्ड AB पर एक बिंदु P इस प्रकार है की PA =a और PB =b यदि AB=a+b हो , तो बिंदु P का बिन्दुपथ ज्ञात कीजिये
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionसिद्ध कीजिए कि बिंदु (1,−6),(5,2),(7,0) तथा (−1,−4)एक चक्रीय चतर्भुज के शीर्ष है ।
View Solutionयदि ¯¯¯¯¯¯OA=¯a,¯¯¯¯¯¯OB=¯b तथा C,AB पर एक ऐसा बिंदु है कि ¯¯¯¯¯¯AC=3¯¯¯¯¯¯AB तो सदिश ¯¯¯¯¯¯OC बराबर है:
View Solutionयदि ¯a,¯b दो सदिश इस प्रकार है कि ∣∣¯a+¯b∣∣=|¯a|, तो सिद्ध कीजिए कि 2¯a+¯b सदिश ¯b पर लम्ब है |
View Solutionएक बिंदु इस प्रकार गमन करता है कि उसकी बिंदु (3,4) से दुरी बिंदु (−3,−4) से उसकी दूरी की तिगुनी रहती है । उसका बिन्दुपथ ज्ञात कीजिए ।
View Solutionयदि f:R→R इस प्रकार है कि f(x) = |x|, तो सिद्ध कीजिए कि fof = f .
View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
View Solutionयदि एक सममित आव्यूह A तथा एक विषम सममित आव्यूह B इस प्रकार है कि A+B=[235−1] तो AB बराबर है
View Solution
