AB एक रेखाखण्ड है और P इसका लम्ब-बिन्दु है | D और E रेखाखण्ड AB के एक ही ओर स्थित दो बिन्दु इस प्रकार है कि ∠BAD -= ∠ABE और ∠EPA -= ∠DPB है | ( देखिए आकृति ) दर्शाइए कि-
(i) ΔDAP ~-= ΔEBP
(ii) AD -= BE
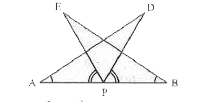
The correct Answer is:AD-=BE
Topper's Solved these Questions
- BOOK - SCIENCE PUBLICATIONCHAPTER - त्रिभुज EXERCISE - प्रश्नावली 7.28videos
त्रिभुज
- BOOK - SCIENCE PUBLICATIONCHAPTER - त्रिभुज EXERCISE - प्रश्नावली 7.35videos
त्रिभुज
- BOOK - SCIENCE PUBLICATIONCHAPTER - त्रिभुज EXERCISE - प्रश्नावली 7.46videos
त्रिभुज
- BOOK - SCIENCE PUBLICATIONCHAPTER - चतुर्भुज EXERCISE - प्रश्नावली 8.2 पर आधारित अभ्यास प्रश्न7videos
चतुर्भुज
- BOOK - SCIENCE PUBLICATIONCHAPTER - दो चरों वाले रैखिक समीकरणEXERCISE - प्रश्नावली 4.4 पर आधारित अभ्यास प्रश्न1videos
दो चरों वाले रैखिक समीकरण
Similar Questions
एक समद्धिबाहू त्रिभुज ABC में जिसमे AB -= AC है, ∠B और ∠C के समद्धिभाजक परस्पर बिन्दु O पर प्रतिच्छेद करते है | A और O को जोडिए | दर्शाइए कि
(i) OB -= OC
(ii) AO कोण A को समद्धिभाजित करता है |05:41View SolutionΔABC और ΔDBC एक ही आधार BC पर बने दो समद्धिबाहू त्रिभुज इस प्रकार है कि A और D भुजा BC के एक ही ओर स्थित है | (देखिए आक्रति ) | यदि AD बढ़ाने पर BC को P पर प्रतिच्छेद करे, तो दर्शाइए कि-
(i) ΔABD ~-= ΔACD
(ii) ΔABP ~-= ΔACP
(iii) AP कोण A और कोण D दोनों को समद्धिभाजित करता है |
(iv) AP रेखाखण्ड BC का लम्ब समद्धिभाजक है |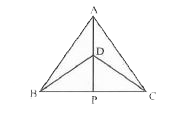
03:33View Solutionदर्शाइए क समकोण त्रिभुज में कोण सबसे लम्बी भुजा होती है |
03:24View SolutionP, Q और R क्रमशः एक समबाहु त्रिभुज ABC की भुजाओं BC, CA और AB के मध्य बिन्दु है। सिद्ध कीजिए कि ΔPQR भी एक समबाहु त्रिभुज हैं।
03:36View Solutionनिम्नलिखित समीकरणों को (i) संख्या रेखा और तथा (ii) कार्तिए तल पर प्रदर्शित कीजिए।
(a) x−2=0 " (b)2x+4=3x+1
(c) y+5=005:38View SolutionMatch the following Column A to Column B
05:05View SolutionAB is a line segment and P is its midpoint. D and E are points on the same side of AD such that ∠BAD=∠ABEand∠EPA=∠DPB.
Show that (i) ΔDAP≅ΔEBP,
(ii)AD=BE.
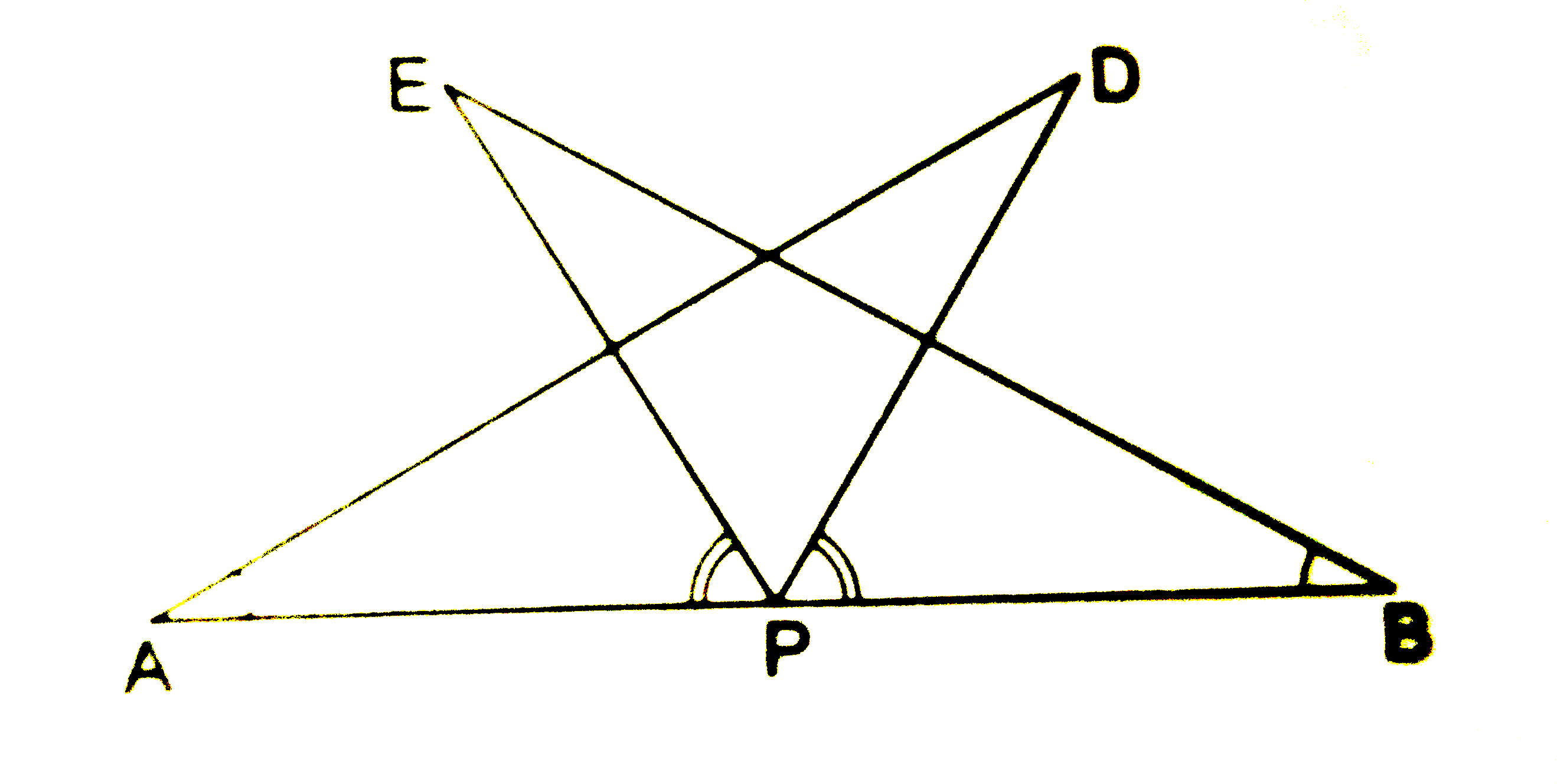
04:32View SolutionAB एक रेखाखंड है और P इसका मध्य बिंदु है | D और E रेखाखंड AB के एक ही ओर स्थित दो बिंदु इस प्रकार हैं कि ∠BAD=∠ABE और ∠EPA=∠DPB है | (देखिए चित्र) | दर्शाइए कि
(i) ΔDAP≅ΔEBP
(ii) AD = BE
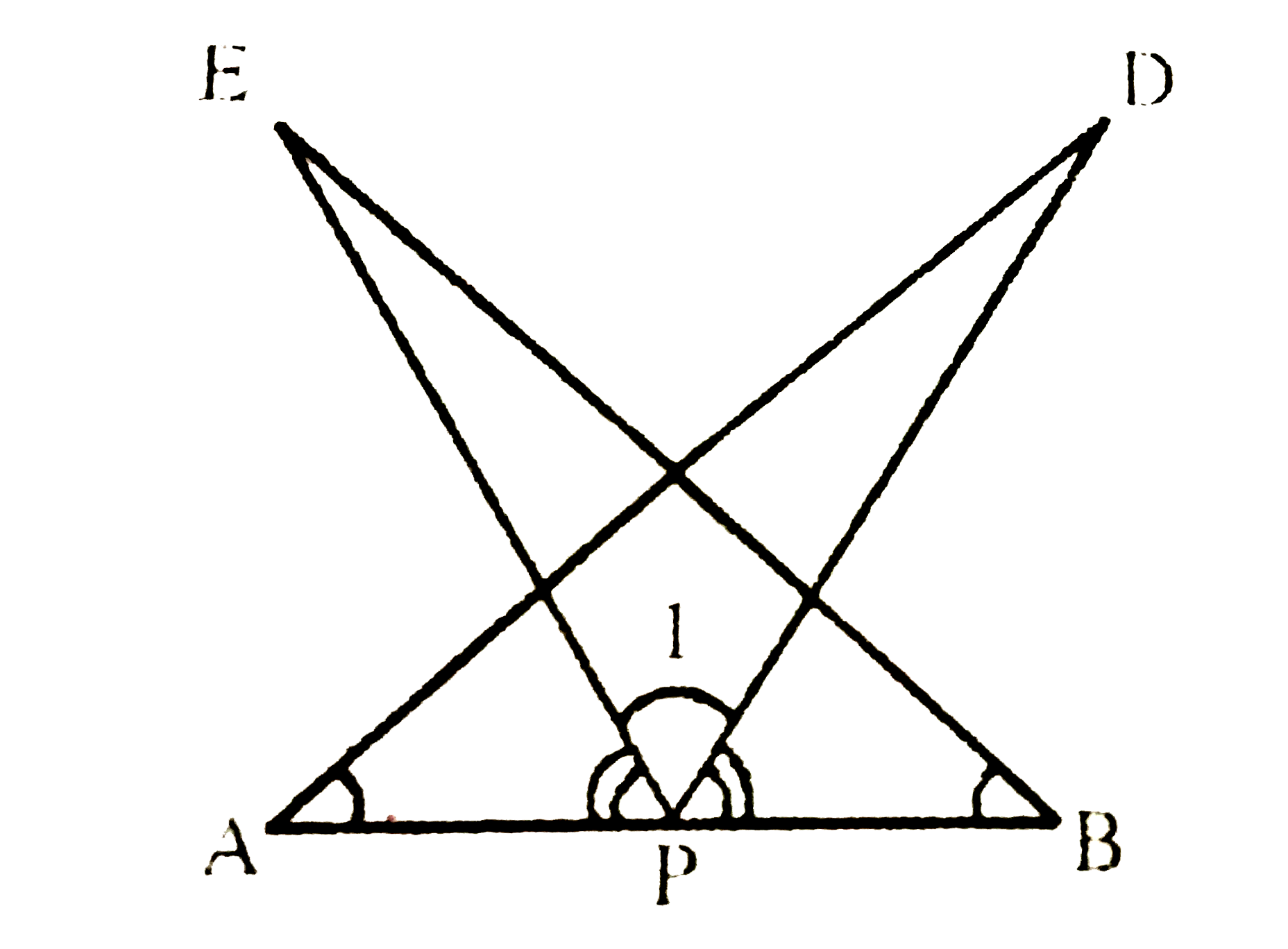
02:29View SolutionAB एक रेखाखण्ड है तथा P इसका मध्यबिंदु है और AB की समान भुजा पर बिंदु D व E इस प्रकार है कि ∠BAD=∠ABE तथा ∠EPA=∠DPB तो सिद्ध कीजिए कि : ΔDAP≅ΔEBP
02:34View SolutionA और B दो बिंदु है। बिंदुओं A और B के स्थिति क्रमशः 6¯a−2¯b और ¯b−9¯a है। वह अनुपात ज्ञात कीजिए जिसमें बिंदु P जिसका स्थिति सदिश ¯a−¯b है रेखाखण्ड AB को विभाजित करता है।
02:00View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
03:06View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
01:03:07View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
07:19View Solutionयदि बिन्दु P(−3,4) से होकर जाने वाली एक सरल रेखा इस प्रकार है कि इसके निर्देशांक अक्षो के बीच अंत: खंडित भाग का मध्य -बिन्दु P है, तो इसका समीकरण है
01:56View Solutionएक बिन्दु पर क्रियाशील दो बल P और Q का अधिकतम परिणामी बल ........ होता है।
03:59View Solution