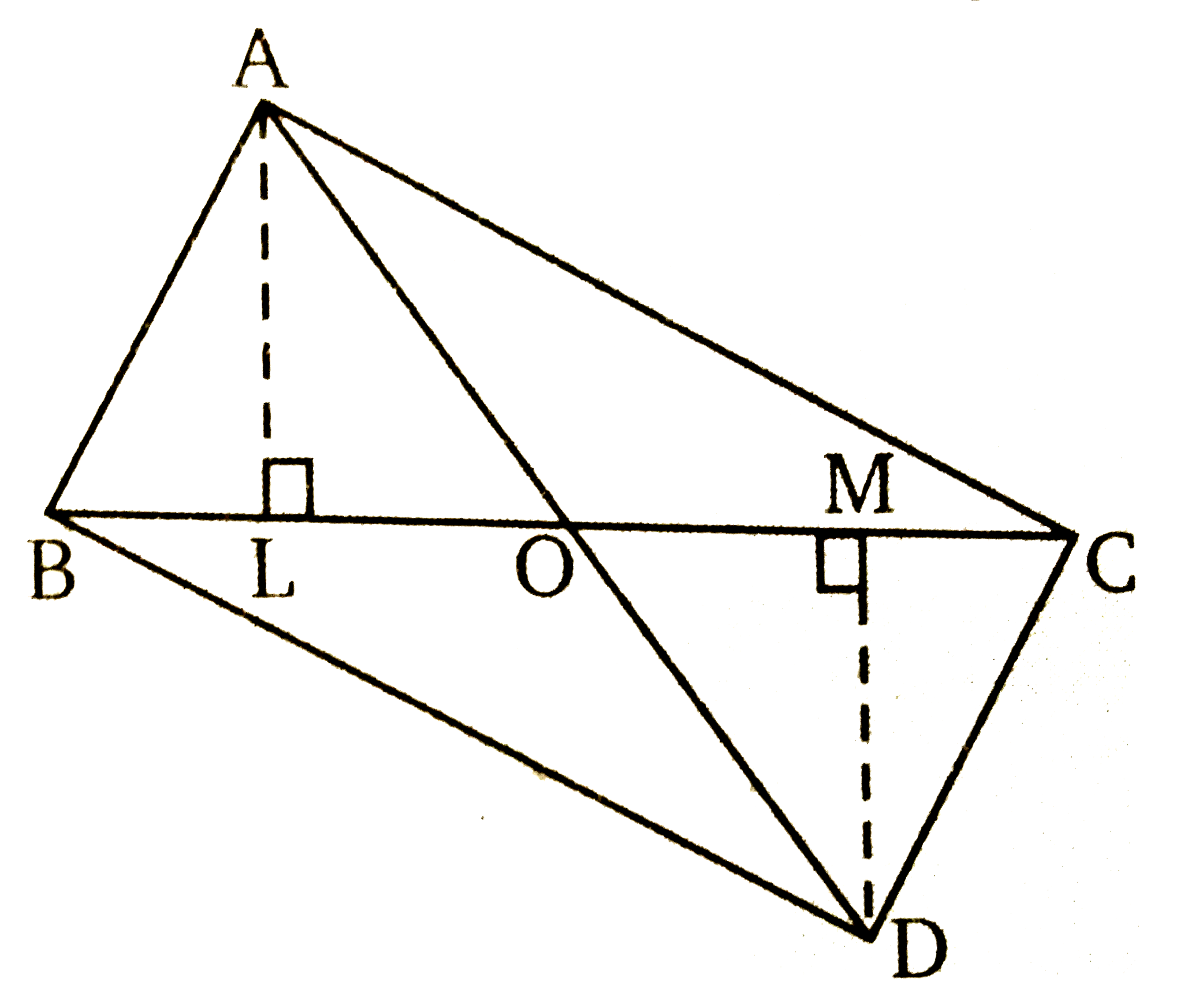
माना ABC व DBC समान आधार BC पर दो त्रिभुज हैं। BC की विपरीत दिशा से A व D बिंदु इस प्रकार हैं कि ar(ΔABC)=ar(ΔDBC)। सिद्ध कीजिए यह BC,AD को समद्विभाजित करती है।
रचना: AL⊥BC व DM⊥BC खींचे।
उपपत्ति: ar(ΔABC)=ar(ΔDBC) (दिया है)
⇒BC×AL2=BC×DM2
⇒AL=DM
अब ΔOAL व ΔOMD में
AL=DM [समीकरण 1 से]
→ALO=∠DMO [प्रत्येक =90∘]
∠AOL=∠MOD [शीर्षाभिमुख कोण]
ΔOAL≅ΔOMD [SAS सर्वांगसमता से]
अतः OA=OD
अतः BC,AD को समद्विभाजित करती है। [CPCT से],
Topper's Solved these Questions
- समांतर चतुर्भुज व त्रिभुज के क्षेत्रफलBOOK - BALAJI PUBLICATIONCHAPTER - समांतर चतुर्भुज व त्रिभुज के क्षेत्रफलEXERCISE - अति लघु उत्तरीय प्रश्न
5 Videos
- समांतर चतुर्भुज व त्रिभुज के क्षेत्रफलBOOK - BALAJI PUBLICATIONCHAPTER - समांतर चतुर्भुज व त्रिभुज के क्षेत्रफलEXERCISE - लघु उत्तरीय प्रश्न
16 Videos
- शेषफल प्रमेय तथा गुणनखण्ड प्रमेय BOOK - BALAJI PUBLICATIONCHAPTER - शेषफल प्रमेय तथा गुणनखण्ड प्रमेय EXERCISE - स्वमूल्यांकन परिक्षण
20 Videos
- सांख्यिकीBOOK - BALAJI PUBLICATIONCHAPTER - सांख्यिकीEXERCISE - स्वमूल्यांकन परीक्षण
17 Videos
Similar Questions
एक समांतर चतुर्भुज के विकर्ण इसे कितने भागों में विभक्त करते हैं?
View Solutionचित्र (i) और (ii) में दिए गये समलम्ब चतुर्भुजों ABCD और PQRS का क्षेत्रफल ज्ञात कीजिए।

View Solutionx3+3x2+3x+1 को 5+2x से भाग करने पर शेषफल ज्ञात कीजिए।
View Solutionतीन सिक्के 30 बार उछाले गये। प्रत्येक बार आये चित् की संख्या निम्न प्रकार लिखी गयी :
0,1,2,2,1,2,3,1,3,0,1,3,1,1,2,2,0,1,2,1,3,0,0,1,1,2,3,2,2,0
उपरोक्त आँकड़ों के लिए एक बारंबारता बंटन सारणी तैयार कीजिए।
View SolutionIn Fig. 6.44, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that (ar (ABC))/( ar (DBC))= (AO )/( DO )
View SolutionIn the given figure, ΔABCandΔDBC have the same base BC. If AD and BC intersect at O, prove that ar(ΔABC)ar(ΔDBC)=AODO
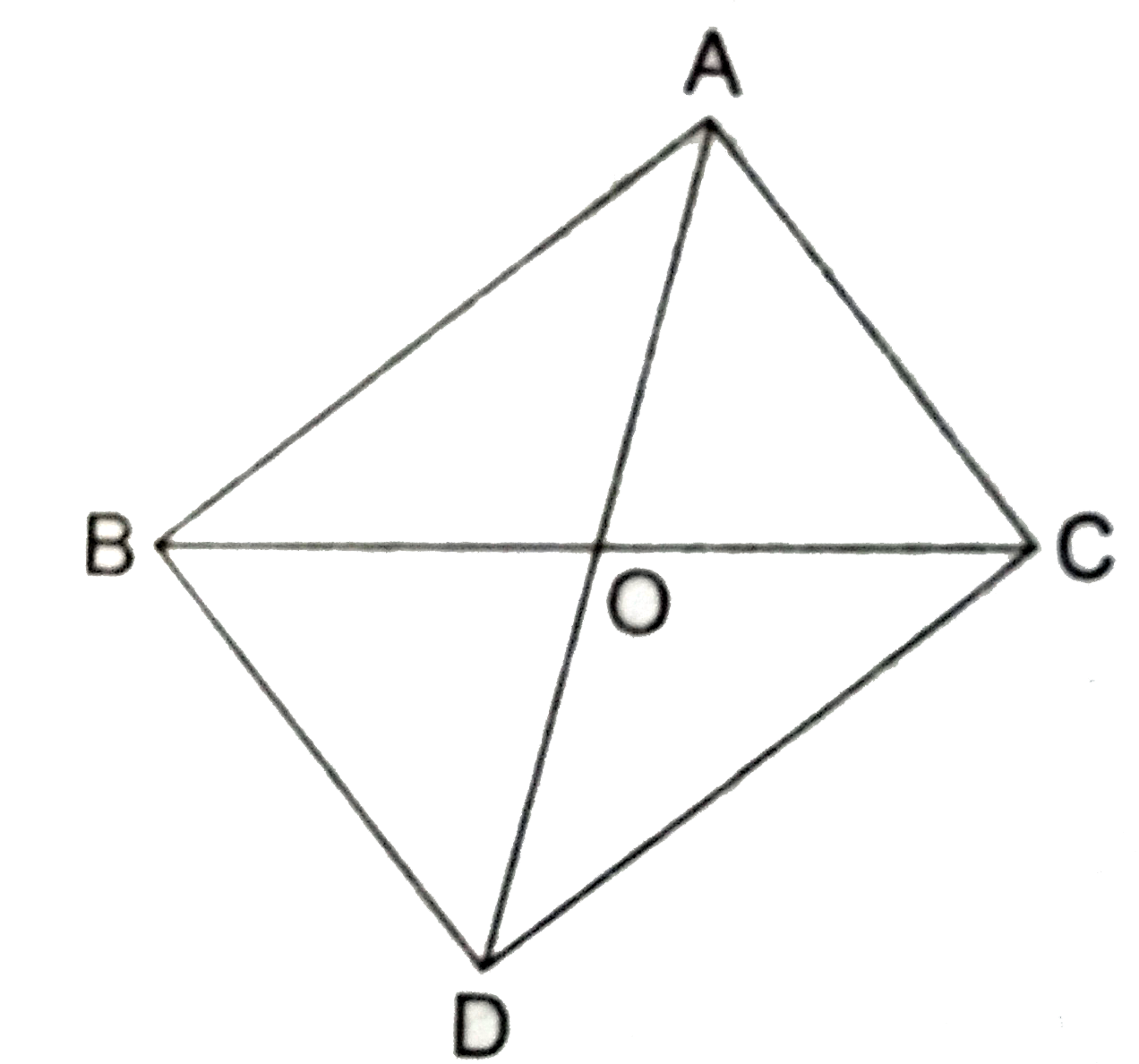
View Solutionआकृति में एक ही आधार BC पर दो त्रिभुज ABC और DBC बने हुए है। यदि AD,BD को O पर प्रतिच्छेद पर तो दर्शाइए कि ar(ΔABC)ar(ΔDBC)=AODO है।
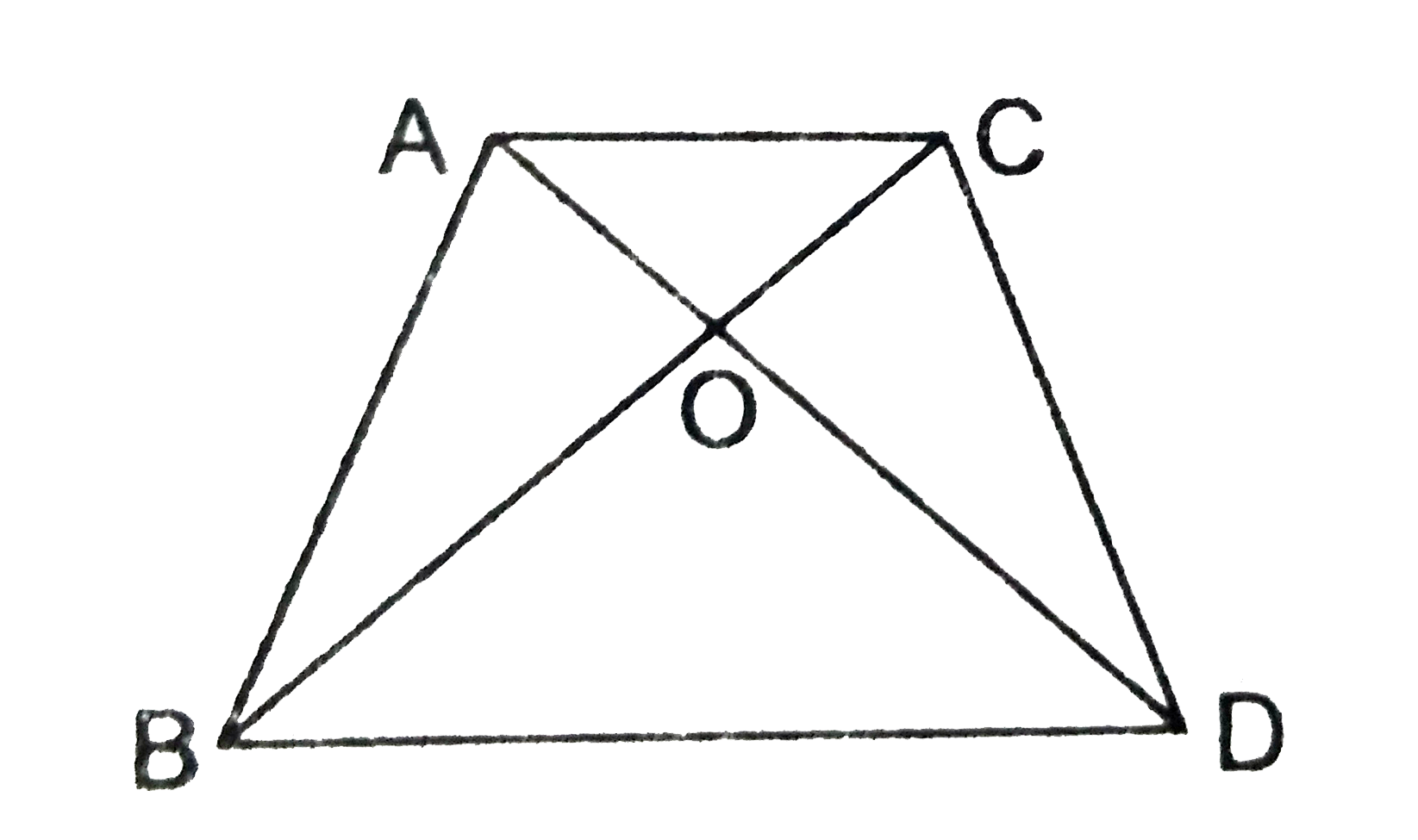
View Solutionएक ही आधार BC पर दो त्रिभुज ABC तथा DBC इस प्रकार स्थित है कि बिंदु A तथा D रेखा BC के विपरीत दिशाओं में है। यदि ar(ΔABC)=ar(ΔDBC) हो, तो दर्शाइए कि BC रेखा AD को समद्विभाजित करती है।
View Solutionदो त्रिभुजों ABC व DBC के आधार समान हैं तथा सम्मुख भुजा BC पर शीर्ष A व D इस प्रकार हैं कि ar(ΔABC)=ar(ΔDBC)। सिद्ध कीजिए कि BC, रेखा AD को समद्विभाजित करती है।
View Solutionत्रिभुज ABC और ΔDBCएक ही आधार BC पर बने दो समद्विबाहु त्रिभुज इस प्रकर हैं कि शीर्ष A और B भुजा BC के एक ही ओर स्थित हैं | यदि AD को बढ़ाने पर वह BC को P पर प्रतिच्छेदित सिध्द करो AP,angleA को समद्विभाजित करता है |
View SolutionIn Fig , ABC and DBC are two triangles on the same base BC. If AD intersects BC,at O , show that ar(ABC)ar(DBC)=AODO
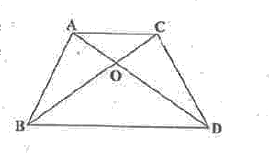
View SolutionIn the figure D, E are points on the sides AB and AC respectively of ΔABC such that ar(ΔDBC)=ar(ΔEBC) . Prove that DE || BC.
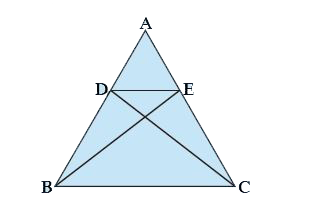
View SolutionIn the figure D, E are points on the sides AB and AC respectively of ΔABC such that ar(ΔDBC)=ar(ΔEBC) . Prove that DE || BC.
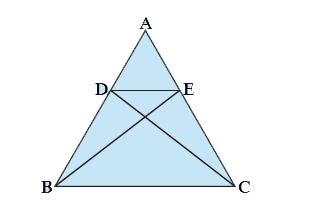
View SolutionIn the figure D, E are points on the sides AB and AC respectively of ΔABC such that ar(ΔDBC)=ar(ΔEBC) . Prove that DE || BC.
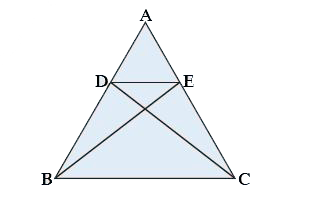
View SolutionIn the given figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that ar(ABC)ar(DBC)=AODO.
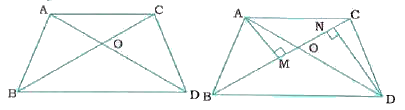
View Solution
