A (3,4),B(−3,0)andC(7,−4) are the vertices of a triangle. Show that the line joining the mid-points of ABandAC is parallel to BC and is half of it.
Step by step video & image solution for A (3,4), B (-3,0) and C(7,-4) are the vertices of a triangle. Show that the line joining the mid-points of AB and AC is parallel to BC and is half of it. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
The vertices of a ΔABC are A(-3,2) . B (-1,-4) and C(5,2) . If M and N are the mid-points of AB and AC res.ly. Show that 2MN = BC.
View SolutionThe mid points of the sides AB and AC of a triangle aBC are (2,−1) and (−4,7) respectively, then the length of BC is
View SolutionIn ΔABC and ΔDEF , AB = DE, AB∣∣DE, BC = EF and BC∣∣EF. Vertices A, B and C are joined to vertices D, E and F respectively (See fig.)
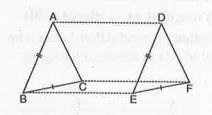 Show that AC=DF.
Show that AC=DF.
View SolutionABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that D is the mid-point of AC.
View SolutionABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that MD⊥AC.
View SolutionABC is a triangle right angled at C and M is mid-point of hypotenuse AB. Line drawn through M and parallel to BC intersects AC at D. Show that:
MD is mid-point of AC.
View SolutionA (5, 3), B (-1, 1) and C (7, -3) are the vertices of triangle ABC. If L is the mid-point of AB and M is the mid-point of AC, show
that : LM=12BC.
View SolutionIn triangle 'ABC,(4,2)' is the mid point of 'AB'. The mid point of 'BC' is '(5,4)', the mid point of 'AC' is '(3,3)'
Draw a rough figure.
Find the vertices of the triangle.
View Solution
