A (5, 3), B (-1, 1) and C (7, -3) are the vertices of triangle ABC. If L is the mid-point of AB and M is the mid-point of AC, show
that : LM=12BC.
To solve the problem, we need to find the midpoints of segments AB and AC, and then show that the length of segment LM is half the length of segment BC.
Step 1: Find the coordinates of midpoint L of segment AB.
The coordinates of points A and B are:
- A(5, 3)
- B(-1, 1)
Using the midpoint formula:
L=(x1+x22,y1+y22)
Substituting the coordinates of A and B:
L=(5+(−1)2,3+12)=(42,42)=(2,2)
Step 2: Find the coordinates of midpoint M of segment AC.
The coordinates of point C are:
- C(7, -3)
Using the midpoint formula for points A and C:
M=(x1+x22,y1+y22)
Substituting the coordinates of A and C:
M=(5+72,3+(−3)2)=(122,02)=(6,0)
Step 3: Calculate the distance LM.
Using the distance formula:
LM=√(x2−x1)2+(y2−y1)2
Substituting the coordinates of L(2, 2) and M(6, 0):
LM=√(6−2)2+(0−2)2=√(4)2+(−2)2=√16+4=√20
Step 4: Calculate the distance BC.
Using the distance formula for points B(-1, 1) and C(7, -3):
BC=√(7−(−1))2+(−3−1)2=√(7+1)2+(−4)2=√(8)2+(−4)2=√64+16=√80
Step 5: Show that LM = (1/2) BC.
We have:
LM=√20
BC=√80=√16⋅5=4√5
Now, we can express 12BC:
12BC=12⋅4√5=2√5
Now, we need to compare LM and 12BC:
LM=√20=√4⋅5=2√5
Thus, we have:
LM=12BC
Conclusion:
We have shown that LM=12BC.
---
- A(5, 3)
- B(-1, 1)
L=(x1+x22,y1+y22)
Substituting the coordinates of A and B:
L=(5+(−1)2,3+12)=(42,42)=(2,2)
- C(7, -3)
M=(x1+x22,y1+y22)
Substituting the coordinates of A and C:
M=(5+72,3+(−3)2)=(122,02)=(6,0)
LM=√(x2−x1)2+(y2−y1)2
Substituting the coordinates of L(2, 2) and M(6, 0):
LM=√(6−2)2+(0−2)2=√(4)2+(−2)2=√16+4=√20
BC=√(7−(−1))2+(−3−1)2=√(7+1)2+(−4)2=√(8)2+(−4)2=√64+16=√80
LM=√20
BC=√80=√16⋅5=4√5
Now, we can express 12BC:
12BC=12⋅4√5=2√5
LM=√20=√4⋅5=2√5
Thus, we have:
LM=12BC
We have shown that LM=12BC.
Topper's Solved these Questions
- SECTION AND MID-POINT FORMULABOOK - ICSECHAPTER - SECTION AND MID-POINT FORMULAEXERCISE - EXERCISE 13 (C)
28 Videos
- SECTION AND MID-POINT FORMULABOOK - ICSECHAPTER - SECTION AND MID-POINT FORMULAEXERCISE - QUESTIONS
17 Videos
- SECTION AND MID-POINT FORMULABOOK - ICSECHAPTER - SECTION AND MID-POINT FORMULAEXERCISE - QUESTIONS
17 Videos
- SAMPLE PAPER 5 (MATHEMATICS)BOOK - ICSECHAPTER - SAMPLE PAPER 5 (MATHEMATICS)EXERCISE - SECTION C
8 Videos
- SHARES AND DIVIDENDSBOOK - ICSECHAPTER - SHARES AND DIVIDENDSEXERCISE - Exercise 3(C )
20 Videos
Similar Questions
A(8, -6), B(-4, 2) and C(0, -10) are vertices of a triangle ABC. If P is the mid-point of AB and Q is the mid-point of AC, use co-ordinate geometry to show that PQ is parallel to BC. Give a special name to quadrilateral PBCQ.
View SolutionABC is a triangle in which D is the mid-point of BC and E is the mid-point of AD. Prove that area of BED=14area of ABC.
View SolutionA(7,−1),B(4,1)andC(−3,4) are the vertices of a triangle ABC. Find the equation of a line through the vertex B and the point P in AC, such that AP:CP=2:3.
View SolutionIn the given figure, M is mid-point of AB and DE, whereas N is mid-point of BC and DF. Show that : EF = AC.
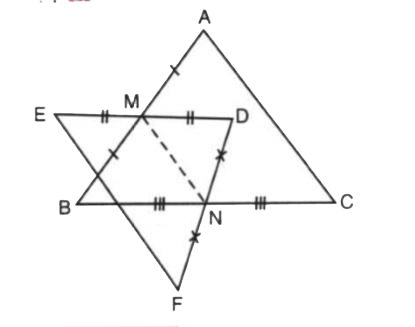
View SolutionIn an equilateral triangle ABC , D is the mid-point of AB and E is the mid-point of AC. Find the ratio between ar (△ABC):ar(△ADE)
View SolutionIn the adjoining figure
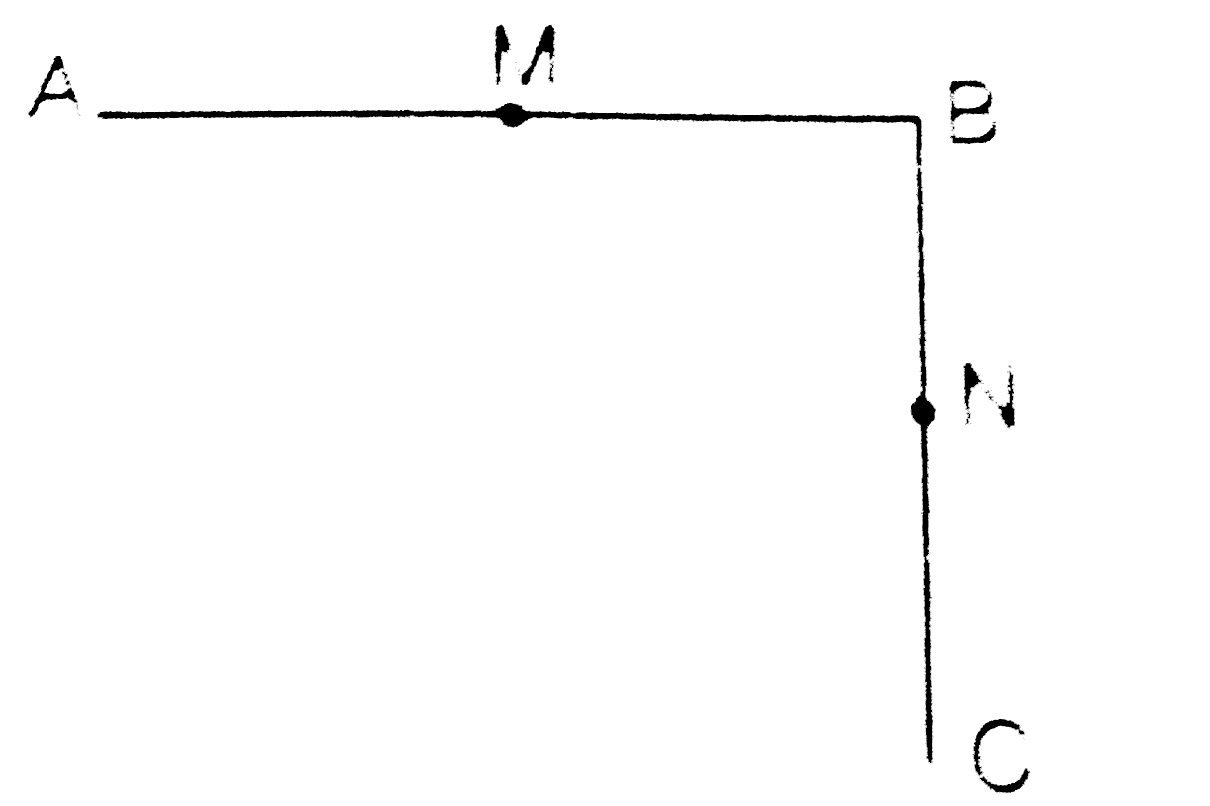
(i) AB=BC, M is the mid -point of AB and N is the mid- point of BC. Show that AM=NC.
(ii) BM=BN,M is the mid- point of AB and N is the mid - point of BC. Show that AB=BC.
View SolutionGiven M is the mid-point of AB, find the co-ordinates of:
B, if A = (3,-1) and M = (-1, 3).
View SolutionA (2, 5), B (-1, 2) and C (5, 8) are the co-ordinates of the vertices of the triangle ABC. Points P and Q lie on AB and AC respectively, such that : AP: PB = AQ: QC = 1:2.
Show that : PQ=13BC.
View SolutionIn a triangle ABC, E is the mid-point of median AD. Show that ar (BED)=14ar (ABC)
View SolutionGiven points A(1,5),B(−3,7)andC(15,9)
Find the equation of a line passing through the mid-point of AC and the point B.
View Solution
