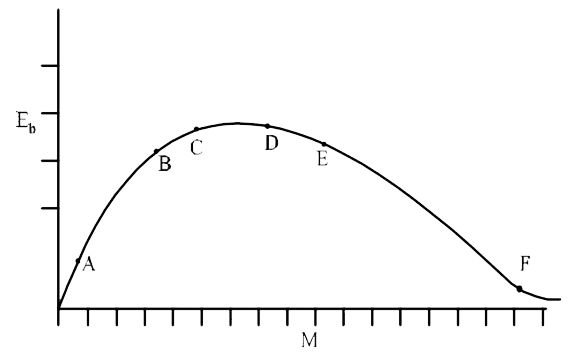
The alongside is a plot of binding energy per nucleon Eb ,against the nuclear mass M,A,B,C,D,E,F correspond to different nuclei. Consider four reactions.
(i) A + B → C +ε (ii) C → A + B + ε
(iii) D + E → F + ε (iv) F → D + E + ε where ε is the energy released. In which reactions , is ε positive?

(i) and (iii)
(ii) and (iv)
(ii)and (iii)
(i) and (iv)
The correct Answer is:D
Energy (ε) is released when lighter nuclei fuse to form a heavier nucleus , such as in (i) A+B→C+ε
Again, energy is released when a heavy nucleus splits into lighter nuclei , such as in (iv) F→D+E+ε.
Topper's Solved these Questions
- NUCLEIBOOK - NCERT FINGERTIPSCHAPTER - NUCLEIEXERCISE - NCERT Exemplar
7 Videos
- NUCLEIBOOK - NCERT FINGERTIPSCHAPTER - NUCLEIEXERCISE - Assertion And Reason
15 Videos
- NUCLEIBOOK - NCERT FINGERTIPSCHAPTER - NUCLEIEXERCISE - Nuclear Energy
10 Videos
- MOVING CHARGES AND MAGNETISM BOOK - NCERT FINGERTIPSCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - Assertion And Reason
15 Videos
- PRACTICE PAPPERBOOK - NCERT FINGERTIPSCHAPTER - PRACTICE PAPPEREXERCISE - Practice Paper 3
50 Videos
Similar Questions
In Fig. 4.101, AD and CE are two altitudes of ABC . Prove that AEF~CDF (ii) ABD~CBE (iii) AEF~ADB (iv) FDC~BEC (FIGURE)
View SolutionA, B, C, D, E, F and G are playing cards sitting in a circle.
(i) F is 2nd to the right of G
(ii) B is neighbour of F but not of E.
(iii) E, the neighbour of C, is 4th to the right of G.
(iv) D is between E and A.
Who is fourth to the left of G?
View Solution
Knowledge Check
The above is a plot of binding energy per nucleon Eb against the nuclear mass M,A,B,C,D,E,F correspond to different nuclei Consider four reactions:AA+B→C+εBC→A+B+εCD+E→F+εandDF→D+E+ε,The above is a plot of binding energy per nucleon Eb, against the nuclear mass M, A, B, C, D, E, F correspond to different nuclei. Consider four reactions
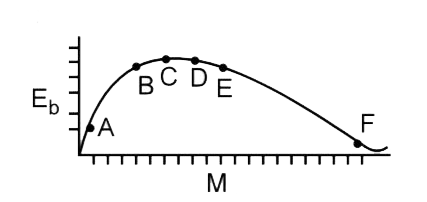
(i) A+B→C+ɛ (ii) C→A+B+ɛ
(iii)D+E→F+ɛ and (iv) F→D+E+ɛ
Where ɛ is the energy released ? In which reactions is positive.A(i) and (iv)B(i) and (iii)C(ii) and (iv)D(ii) and (iii)The dimensions of 12∈0E2, where ∈0 is permittivity of free space and E is electric field, is :-
A[M1L1T−2A1]B[M1L0T−1]C[M1L−1T−2A1]D[M1L−1T−2]
ABCD is a parallelogram and EandF are the centroids of triangles ABD and BCD respectively, then EF= (a)AE (b) BE (c) CE (d)DE
View SolutionD, E, F are the mid-point of the sides BC, CA and AB respectively of ABC. Then DEF is congruent to triangle. ABC (b) AEF (c) BFD, CDE (d) AFE, BFD, CDE
Given : D, E, F are the mid-point of the sides BC, CA and AB .
View SolutionAt a temperature of 0K, the total energy of a gaseous diatomic molecule AB is approximately given by:
E=Eo+Evib
where Eo is the electronic energy of the ground state, and Evib is the vibrational energy.
Allowed values of the vibrational energies are given by the expression:
Evid=(v−12)ε v=0,1,2,....... ε=h2π√kμ μ(AB)=mAmBmA+mB
where h is the planck's constant, is the vibration quantum number, k is the force constant, and is the reduced mass of the molecule. At 0K, it may be safely assumed that is zero, and Eo and k are independent of isotopic substitution in the molecule.
Deuterium, D, is an isotope of hydrogen atom with mass number 2. For the H2 molecule, k is 575.11Nm−1, and the isotopic molar masses of H and D are 1.0078 and 2.0141gmol−1, respectively.
At a temperature of 0K:εH2=1.1546εHD and εD2=0.8167εHD
Calculate––––––––––– the electron affinity, EA, of H+2 ion in eV if its dissociation energy is 2.650eV. If you have been unable to calculate the value for the dissociation energy of H2 then use 4.500eV for the calculate.
View SolutionIf a, b, c, d, e, f are in A.P. then e - c is equal to
View SolutionThe dimension of (12)ε0E2 (ε0 : permittivity of free space, E electric field
View Solution
