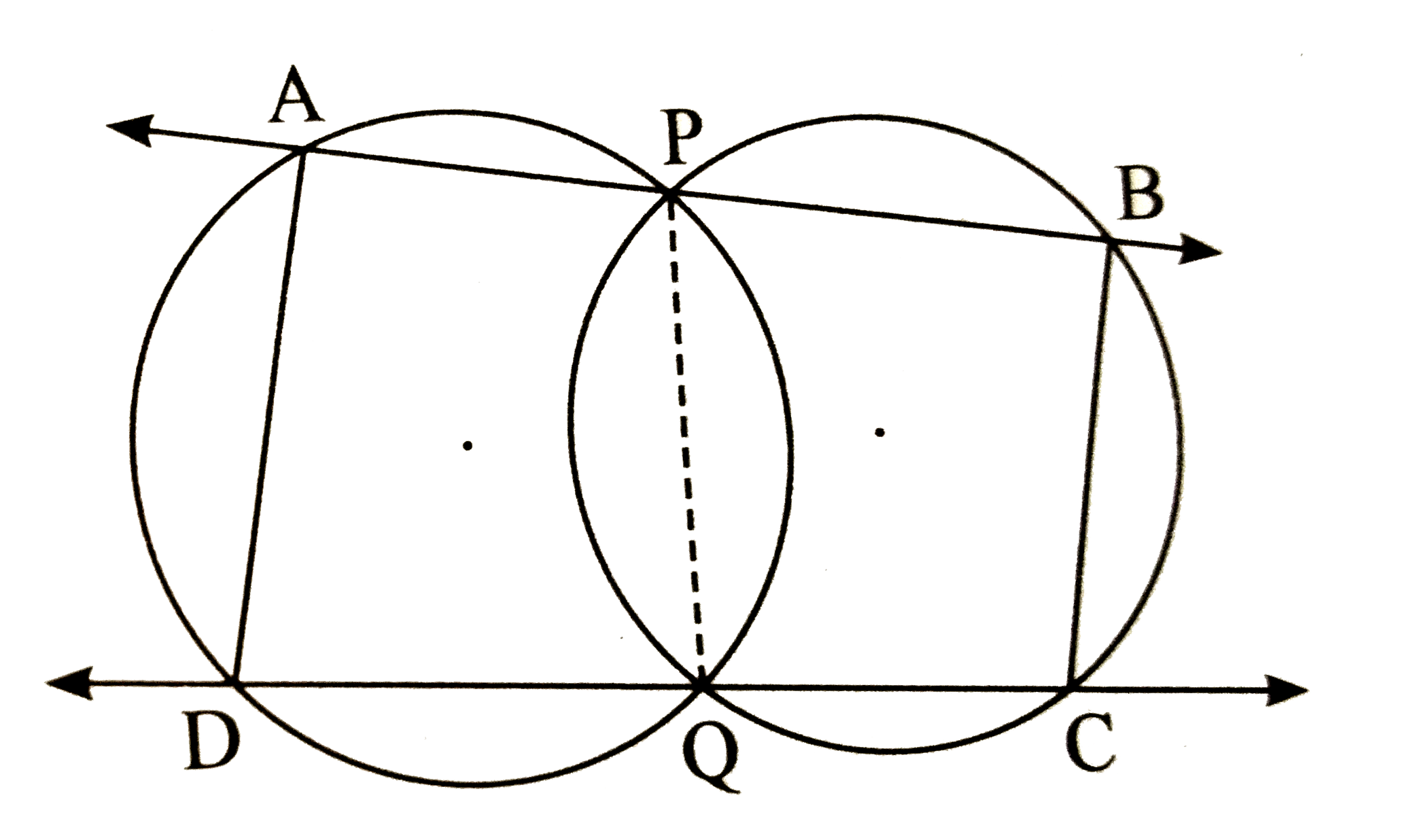
In the adjoining figure , two circles intersect each other at the points P and Q. If ∠QAD=80∘and∠PDA=84∘, then find the value of ∠QBCand∠BCP Solution in Bengali
In the circle with center at O, ADPQ is a cyclic quadrilateral.
∴∠ADP+∠AQP=180∘ or 84∘+∠AQP=180∘[∵∠ADP=84∘]
or, ∠AQP=180∘−84∘=96∘
Now , ∠BQP+∠AQP=1straight angle
or, ∠BQP+96∘=180∘[∵∠AQP=96∘]or ∠BQP=180∘−96∘=84∘
Again , BQPC is a cyclic quadrilateral.
∴∠BCP+∠BQP=180∘ or ,∠BCP+84∘=180∘
or, ∠BCP=180∘−84∘=96∘
Now , ∠DPQ+∠DAQ=180∘ or ,∠DPQ+80∘=180∘ or ,∠DPQ=180∘−80∘=100∘
∴∠DPQ+∠QPC=1 straight angle =180∘
or 100∘+∠QPC=180∘ or ,∠QPC=180∘−100∘=80∘
Again , ∠QPC+∠QBC=180∘[∵ BQPC is a cyclic quadrilateral]
or, 80∘+∠QBC=180∘ or,∠QBC=180∘−80∘=100∘.
Hence ∠QBC=100∘and∠BCP=96∘

Topper's Solved these Questions
- THEOREMS RELATED TO CYCLIC QUADRILATERAL BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CYCLIC QUADRILATERAL EXERCISE - Example (Long-answer type questions)
20 Videos
- THEOREMS RELATED TO CYCLIC QUADRILATERAL BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CYCLIC QUADRILATERAL EXERCISE - EXERCISE-3(Very short - answer type questions)(MCQ)
4 Videos
- THEOREMS RELATED TO CYCLIC QUADRILATERAL BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CYCLIC QUADRILATERAL EXERCISE - Fill in the blanks:
6 Videos
- THEOREMS RELATED TO CIRCLE BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CIRCLE EXERCISE - EXERCISE - 1 (Long - answer type question )
9 Videos
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXERCISE 2.3 (Long Answer Type Questions)
14 Videos
Similar Questions
In the adjoining figure , the diagonals of the cyxlic quadrilateral PQRS intersect each other at the point X in such a way that ∠PRS=65∘and∠ROS=45∘. Find the values of ∠SQPand∠RSP .
View SolutionIf the length of diagonal of a square is √72cm, then calculate the area of the square.
View SolutionAll angles in the same segment are……….
View SolutionProve that diameter is the greatest chord of a circle.
View SolutionProve that angle in the segment of a circle which is greater than a semi-circle is an acute angle.
View SolutionAs per the figure, two circles intersect each other at points P and Q. Point A is on PQ produced and AMD and ASR are the secants to the circles. If AM = 3, MD = 5, AS = 4, The value of SR is :
View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect one circle at the points A and C and the other circle at B and D. Prove the AC|| BD
View SolutionTwo circles intersect each other at point P and Q. Secants drawn through p and Q intersect the circles at points A,B and D,C
Prove that :∠ADC+∠BCD=180∘
View SolutionIn the adjoining figure, O is the centre of a circle and AB is one of its diameters. The legth of the chrod CD is equal to the radius of the circle. When AC and BD are extended, they intersect each other at a point P. find the value of ∠APB
View SolutionIn the adjoining figure, two circles with centres P and Q intersect each other at the points B and C, ACD is a line segment . If ∠ARS=150∘and∠BQC=x∘ , then find the value of x.
View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect on circle at the points A and C and the other circle at B and D . Prove that AC||BD.
View SolutionTwo chords AC and BD of a circle intersect each other at the point O. If two tangents drawn at the points A and B intersect each other at the point P and two tangents drawn at the points C and D intersect at the point Q, prove that ∠P+∠Q=2∠BOC.[GP−X]
View SolutionIn the figure, two circles intersect each other in points P and Q. If tangent from point R touch the circles at S and T, then prove that RS=RT.

View SolutionIn the adjoining figure, two circles intersect each other at points M and N . Secants drawn from points M and N intersect cirecls at point R, S, P and Q as shown in the figure.
View SolutionIn the adjoining figure, two circles intersect each other at points A and E . Their common secant through E intersects the circle at points B and D . The tangents of the circles at point B and D intersect each other at point C . Prove that □ABCD is cyclic .

View Solution
