AOB is a diameter of a circle with centre O and C is any point on the circle, joining A, C, B, C, and O, C, prove that
tan∠ABC=cot∠ACOSolution in Bengali
since AOB is a diameter and C is any point on the circle,
∴∠ACB is a semicircular angle.
∴∠ACB=90∘
∴ AB is a hypotenuse of the right-angled triangle ABC.
Again, since ∠ACB=90∘,∴∠BAC+∠CBA=90∘.
Now, (a) tan∠ABC=tan(90∘−∠CAB)
=cot∠CAB..................(1)
Again, in ΔAOC,OA=OC[∵ radii of same circle]
⇒∠OAC=∠ACO
⇒∠CAB=∠ACO
∴ from (1) we get, tan∠ABC=cot∠ACO.
Topper's Solved these Questions
- BOOK - CALCUTTA BOOK HOUSECHAPTER - TRIGONOMETRIC RATIOS OF COMPLEMENTARY ANGLES EXERCISE - EXERCISE28videos
TRIGONOMETRIC RATIOS OF COMPLEMENTARY ANGLES
- BOOK - CALCUTTA BOOK HOUSECHAPTER - TRIGONOMETRIC RATIOS AND TRIGONOMETRIC IDENTITIES EXERCISE - EXERCISE66videos
TRIGONOMETRIC RATIOS AND TRIGONOMETRIC IDENTITIES
- BOOK - CALCUTTA BOOK HOUSECHAPTER - VARIATIONEXERCISE - EXERCISE59videos
VARIATION
Similar Questions
If A, B, C are the angles of a triangle then tan(B+C2)=
04:50View SolutionIf tanθ=pq, what is the value of psecθ−q cosecθpsecθ+q cosecθ=
05:22View SolutionIf a ∝1b, then
04:11View SolutionOA is the radius of a circle with centre at Q, AQ is its chrod and C is any point on the circle. A circle passes through the point O,A,C intesect the chrod AQ at the point P. Prove that CP=PQ
04:30View SolutionAOB is a diameter of a circle with centre O and C is any point on the circle, joining A, C, B, C, and O, C, prove that
sin2∠BCO+sin2∠ACO=104:54View SolutionAOB is a diameter of a circle with centre O and C is any point on the circle, joining A, C, B, C, and O, C, prove that
cosec2∠CAB−1=tan2∠ABC.05:47View SolutionIf a line intersects two concentric circles ( circles with the same centre ) with centre O at A, B, C and D, prove that AB = CD.
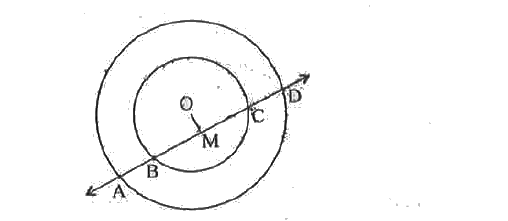 05:36View Solution
05:36View SolutionO কেন্দ্রীয় যে-কোনো একটি বৃত্তের AOB একটি ব্যাস এবং বৃত্তের উপর C যে-কোনো একটি বিন্দু | এবার A,C, B,C এবং O,C যুক্ত করে দেখাও যে, tan∠ABC=cot∠ACO
02:08View SolutionO কেন্দ্রীয় যে-কোনো একটি বৃত্তের AOB একটি ব্যাস এবং বৃত্তের উপর C যে-কোনো একটি বিন্দু | এবার A,C, B,C এবং O,C যুক্ত করে দেখাও যে, sin2∠BCO+sin2∠ACO=1
04:59View SolutionO কেন্দ্রীয় যে-কোনো একটি বৃত্তের AOB একটি ব্যাস এবং বৃত্তের উপর C যে-কোনো একটি বিন্দু | এবার A,C, B,C এবং O,C যুক্ত করে দেখাও যে, cosec2∠CAB−1=tan2∠ABC
03:35View SolutionIf two chords AB and AC of a circle with centre O are such that the centre O lies on the bisector of ∠BAC, prove that AB=AC , i.e. the chords are equal.
03:18View SolutionIn Figure, ˆAB≅ˆAC and O is the centre of the circle. Prove that OA is the perpendicular bisector of BC
02:26View SolutionIn Figure, AB=CB and O is the centre of the circle. Prove that BO bisects ∠ABC.
02:00View SolutionAB is a diameter of a circle with centre O and radius OD is perpendicular to AB. If C is any point on arc DB, find ∠BAD and ∠ACD.
02:10View SolutionDraw a circle with centre O and any radius. Draw AC and BD two perpendicular diameters of the circle. Join AB, BC, CD and DA .
02:36View Solution

