AOB is a diameter of a circle with centre O and C is any point on the circle, joining A, C, B, C, and O, C, prove that
cosec2∠CAB−1=tan2∠ABC.Solution in Bengali
since AOB is a diameter and C is any point on the circle,
∴∠ACB is a semicircular angle.
∴∠ACB=90∘
∴ AB is a hypotenuse of the right-angled triangle ABC.
Again, since ∠ACB=90∘,∴∠BAC+∠CBA=90∘.
cosec2∠CAB−1
=cot2∠CAB
=cot2(90∘−∠ABC)
=tan2∠ABC.
Hence cosec2∠CAB−1=tan2∠ABC.
Topper's Solved these Questions
- TRIGONOMETRIC RATIOS OF COMPLEMENTARY ANGLES BOOK - CALCUTTA BOOK HOUSECHAPTER - TRIGONOMETRIC RATIOS OF COMPLEMENTARY ANGLES EXERCISE - EXERCISE
28 Videos
- TRIGONOMETRIC RATIOS AND TRIGONOMETRIC IDENTITIES BOOK - CALCUTTA BOOK HOUSECHAPTER - TRIGONOMETRIC RATIOS AND TRIGONOMETRIC IDENTITIES EXERCISE - EXERCISE
66 Videos
- VARIATIONBOOK - CALCUTTA BOOK HOUSECHAPTER - VARIATIONEXERCISE - EXERCISE
59 Videos
Similar Questions
If A, B, C are the angles of a triangle then tan(B+C2)=
View SolutionIf tanθ=pq, what is the value of psecθ−q cosecθpsecθ+q cosecθ=
View SolutionIf a ∝1b, then
View SolutionAOB is a diameter of a circle with centre O and C is any point on the circle, joining A, C, B, C, and O, C, prove that
tan∠ABC=cot∠ACO
View SolutionAOB is a diameter of a circle with centre O and C is any point on the circle, joining A, C, B, C, and O, C, prove that
sin2∠BCO+sin2∠ACO=1
View SolutionIn figure PQ is a tangent at a point C to a circle with centre O. If AB is a diameter and ∠CAB=30∘, find ∠PCA
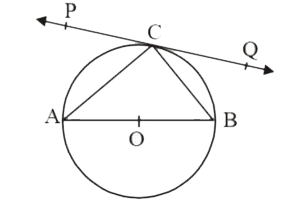
View SolutionIn figure ∠ABC=120∘, where A,B and C are points on the circle with centre O. Find ∠OAC ?

View SolutionIn 2, PQ is a tangent at a point C to circle with centre O. If AB is a diameter and ∠CAB=30∘ then find ∠PCA.

View SolutionAB is a diameter of the circle. C is a point on the circle. angleABC=60^@ If angleCAB Let's determine the value of.
View SolutionO কেন্দ্রীয় যে-কোনো একটি বৃত্তের AOB একটি ব্যাস এবং বৃত্তের উপর C যে-কোনো একটি বিন্দু | এবার A,C, B,C এবং O,C যুক্ত করে দেখাও যে, tan∠ABC=cot∠ACO
View SolutionO কেন্দ্রীয় যে-কোনো একটি বৃত্তের AOB একটি ব্যাস এবং বৃত্তের উপর C যে-কোনো একটি বিন্দু | এবার A,C, B,C এবং O,C যুক্ত করে দেখাও যে, sin2∠BCO+sin2∠ACO=1
View SolutionO কেন্দ্রীয় যে-কোনো একটি বৃত্তের AOB একটি ব্যাস এবং বৃত্তের উপর C যে-কোনো একটি বিন্দু | এবার A,C, B,C এবং O,C যুক্ত করে দেখাও যে, cosec2∠CAB−1=tan2∠ABC
View SolutionIn the Figure, OD is perpendicular to the chord AB of a circle whose centre is O. If BC is a diameter, show that CA=2OD.
View SolutionIf two chords AB and AC of a circle with centre O are such that the centre O lies on the bisector of ∠BAC, prove that AB=AC , i.e. the chords are equal.
View SolutionIn Figure, ˆAB≅ˆAC and O is the centre of the circle. Prove that OA is the perpendicular bisector of BC
View Solution
