A particle retards from a velocity $v_{0}$ while moving in a straight line. If the magnitude od deceleration is directly proportional to thesquare roop of the speed of the particle, find its average velocity for thetotal tome of ist motion.

A

$\frac{v_{0}}{3}$

B

$\frac{3 v_{0}}{2}$

C

$\frac{2 v_{0}}{3}$

D

$\frac{2 v_{0}}{5}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

The average velocity is given as:
$v_{a v} = \frac{S}{t} = \frac{T o t a l d i s p l a c m e n t}{T o t a l t i m e}$
We know $a = v \frac{d v}{d s} \Rightarrow v d v = a d s$
Let us calculate the displacement by substituting $a = - α \sqrt{v}$
(for retardation) in $v d v = a x d s$ .
We have $v d v = - α \sqrt{v}$ ds. $\Rightarrow \sqrt{v} d s = - α d s$
When the particle slows sown from $v_{0}$ to $0$ , it comers a distance $s$ .
Hence, $\int_{v 0}^{0} \sqrt{d} v = - \int_{0}^{s} α$ ds
This gives $s = \frac{2 v_{0}^{3 / 2}}{3 α}$
Use of $a = \frac{d v}{d t}$ : Now we will find the time of motion by substituting $a = - \sqrt{v}$
in $a \frac{d v}{d t}$ , we get
$- α \sqrt{v} = \frac{d v}{d t} \Rightarrow \frac{d v}{\sqrt{v}} = - α d t$
If the particle takes time $t$ to stop, we have
$\int_{v 0}^{0} \frac{d v}{\sqrt{v}} = - α \int_{0}^{t} d t$
This yields $t = \frac{{\sqrt{v}}_{0}}{α}$ .
Finally sunstituting $s$ and (t) in $v_{a v} = \frac{s}{t}$ , we have
$v_{a v} = \frac{2 v_{0}}{3}$ .

|

Updated on:21/07/2023

Class 11 PHYSICS RECTILINEAR MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A particle is moving in a straight line with uniform velocity. Its acceleration is
Apositive
Bnegative
Czero
Dnone of these
Question 2 - Select One
A particle is moving in a straight line with uniform velocity. Its acceleration is
Apositive
Bnegative
Czero
Dnone of these
Question 3 - Select One
A particle is moving on a straight line such that square of its velocity is directly proportional to distance as shown in graph. What is the acceleration of the particle ?

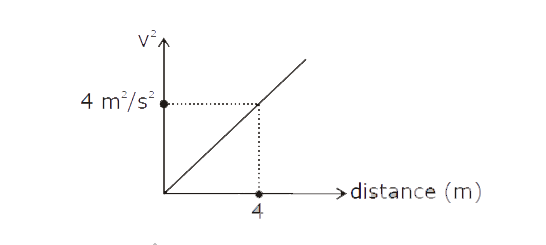A $\frac{1}{4} m / s^{2}$
B $1 m / s^{2}$
C $2 m / s^{2}$
D $\frac{1}{2} m / s^{2}$

CENGAGE PHYSICS-KINEMATICS-1-Solved Examples

Home
Ask Doubt
Profile