Four blocks and two springs are arranged as shown in fig. The system at rest, determine the accelration of all the loads immedialtely after the lower thread keeping the system in equilibrium has been cut. Assume that the threads are weightless, the mass of the pulley is negligible small, and there is no friction at the point of suspension.

For the equilibrium of system of loads,
(m1+m2)>(m3+m4)
The force in the left spring.
Let T2 is the force inthe right spring. For the equlilbrium of load m3, we have
m3g+T2=T0 ..(i)
For m1,m1g+T1=T0

As T1=m2g, therefore,
m1g+m2g=T0
Substituting this value in (i), we get
m3g+T2=(m1g+m2g)
or T2=(m1+m2−m3)g ...(ii)
After cutting, the lower thread, the equations of motion for the loads are
m1g+T1−T0=m1a1 ..(iii)
m2g−T1=m2a2 ...(iv)
T2+m3g−T0=m3a3..(v)
and T2−m4g=m4a4 ...(vi)
Solving above equation, we get
a1=a2=a3=0
and a4=(m1+m2−m3−m4)gm4.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Solved Examples
11 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.1
11 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
For the system at rest shown in Fig., determine the accelerations of all the loads immediately after the lower thread keeping the system in equilibrium has been cut. Assume that the threads are weightless and inextensible, the springs are weightless, the mass of the pulley is negligibly small, and there is no friction at the point of suspension.

View SolutionFind the acceleration of the block of mass m in the arrangement shown in the following figures. The masses of the pulleys and the threads, as well as the friction are assumed to be negligible.

View Solution
Knowledge Check
In arrangement shown below, the thread pulley and spring are all massless and there is no friction anywhere. The system is in equilibrium. If thread connecting m4 is cut then just after thread is cut :
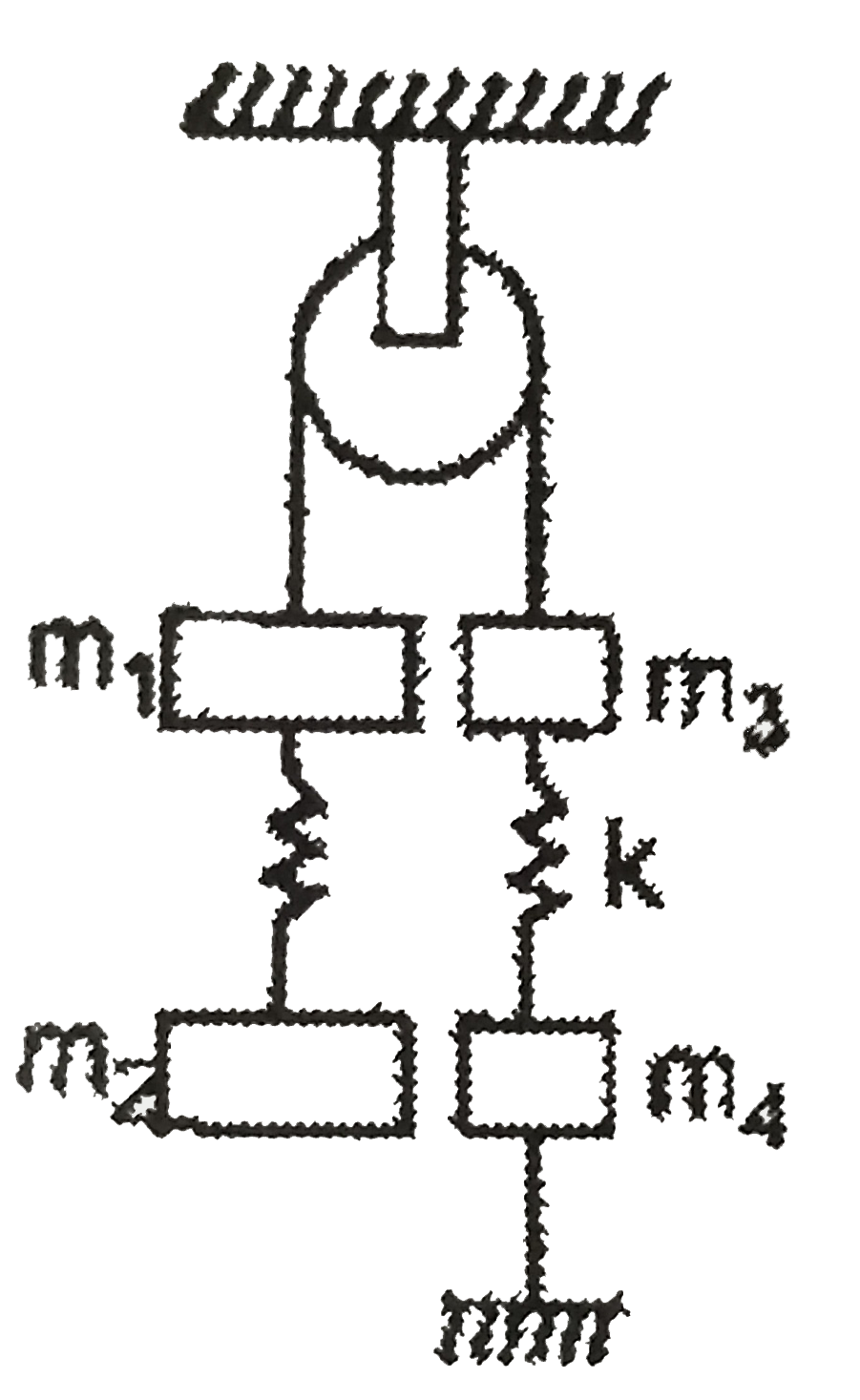 Aacceleration of m4=0Bacceleration of m1=m2=m3=m4=0Cacceleration of m1=m2=m3=0Dacceleration of m4=[(m1+m2)−(m3+m4)]gm4
Aacceleration of m4=0Bacceleration of m1=m2=m3=m4=0Cacceleration of m1=m2=m3=0Dacceleration of m4=[(m1+m2)−(m3+m4)]gm4A mass M is suspended as shown in fig. The system is in equilibrium. Assume pulleys to be massless. K is the force constant of the spring.
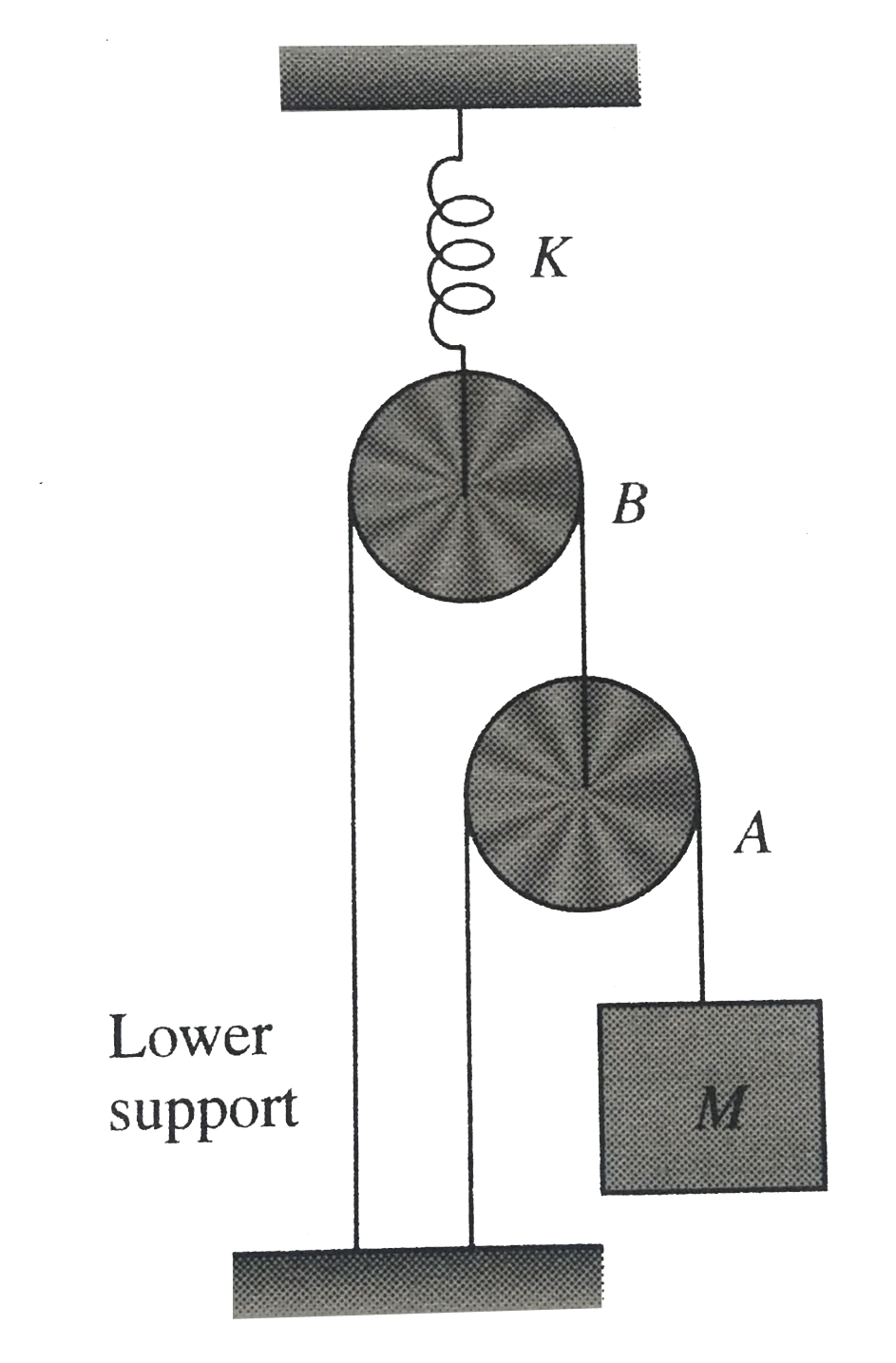
Find the net tension force acting on the lower support.AMgB2MgC3MgD4Mg
Masses m1,m2,m3 and m4 are arranged in a system as shown in fig where m1+m2>m3+m4 The lower string keeping the system in equilibrium is burnt The masses start moving. Find the acceleration of masses if the threads are weightless and inextensible the springs are also weightless and the mass of the pulley is negligible.

View SolutionIn the arrangement shown all pulleys and strings are ideal. A vertical downward force of 10N is needed to apply on block A to keep the system in equilibrium. If mass of B is 10kg then find the mass of A
View SolutionIn the system shown in figure the masses of the bodies are known to be m1 and m2, the coefficient of friction between the body m1 and the horizontal plane is equal to k, and a pulley of mass m is assumed to be a uniform disc. The thread does not slip over the pulley. At the moment t=0 the body m2 starts descending. Assuming the mass of the thread and the friction in the axle of the pulley to be negligible, find the work performed by the friction forces acting on the body m1 over the first t seconds after the beginning of motion.

View SolutionA mass M is suspended as shown in fig. The system is in equilibrium. Assume pulleys to be massless. K is the force constant of the spring.

Find the net tension force acting on the lower support.
View SolutionIf the system is released from rest, determine the speeds of both masses after B has moved 1 m. Neglect friction, the masses of pulleys and inextensible string.
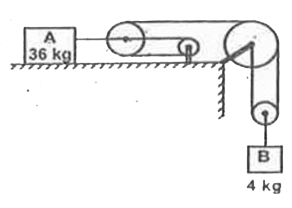
View SolutionIf the system is released from rest, determine the speeds of both masses after B has moved 1 m. Neglect friction, the masses of pulleys and inextensible string.

View Solution
