In the system shown in figure the masses of the bodies are known to be m1 and m2, the coefficient of friction between the body m1 and the horizontal plane is equal to k, and a pulley of mass m is assumed to be a uniform disc. The thread does not slip over the pulley. At the moment t=0 the body m2 starts descending. Assuming the mass of the thread and the friction in the axle of the pulley to be negligible, find the work performed by the friction forces acting on the body m1 over the first t seconds after the beginning of motion.

As the system (m+m1+m2) is under constant forces, the acceleration of body m1 an m2 is constant. In addition to it the velocities and acceleration of bodies m1 and m2 at equal in magnitude (say v and w) because the length of the thread is constant.
From the equation of increament of mechanical energy i.e. ΔT+ΔU=Afr, at time t whe block m1 is distance h below from initial position corresponding to t=0,
12(m1+m2)v2+12(mR22)v2R2−m2gh=−km1gh (1)
(as angular velocity ω=v/R for no slipping of thread).
But v2=2wh
So using it in (1), we get
w=2(m2−km1)gm+2(m1+m2) (2)
Thus the work done by the friction force on m1
Afr=−km1gh=−km1g(12wt2)
=−km1(m1−km1)g2t2m+2(m1+m2) (using 2)
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Elastic Deformation Of Asolid Body25videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Hydrodynamics25videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Universal Gravitation34videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation36videos
OSCILLATIONS AND WAVES
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena38videos
THERMODYNAMICS AND MOLECULAR PHYSICS
Similar Questions
What pressure has to be applied to the ends of a steel cylinder to keep its length constant on raising its temperature by 100.∘C ?
03:59View SolutionIdeal fluid flows along a flat tube of constant cross-section, located in a horizontal plane and bent as shown in figure. (top view). The flow is steady. Are the presssures and velocities of the fluid equal at points 1 and 2? What is the shape of the streamlines?
 15:57View Solution
15:57View SolutionA planet of mass M moves along a circle around the Sun with velocity v=34.9km/s (relative to the heliocentric reference frame). Find the period of revolution of this planet around the Sun.
16:13View SolutionAn electromagnetic wave of frequency v=3.0MHz passes from vacuum into a dielectric medium with permittivity ε=4.0. Then
16:21View SolutionCalculate what fraction of gas molecules
(a) traverses without collisions the distances exceeding the mean free path λ ,
(b) has the free path values lying within the inerval from λ to 2λ.17:57View SolutionTwo bodies with masses m1 and m2(m1>m2) are joined by a string passing over fixed pulley. Assume masses of the pulley and thread negligible. Then the acceleration of the centre of mass of the system (m1+m2) is
06:21View SolutionIn the arrangement of figure the masses m_0 , m_1 , and m_2 of bodies are equal, the masses of the pulley and the threads are negligible, and there is no friction in the pulley. Find the acceleration w with which the body m_0 comes down, and the tension of the thread binding together the bodies m_1 and m_2 , if the coefficient of friction between these bodies and the horizontal surface is equal to k. Consider possible cases.
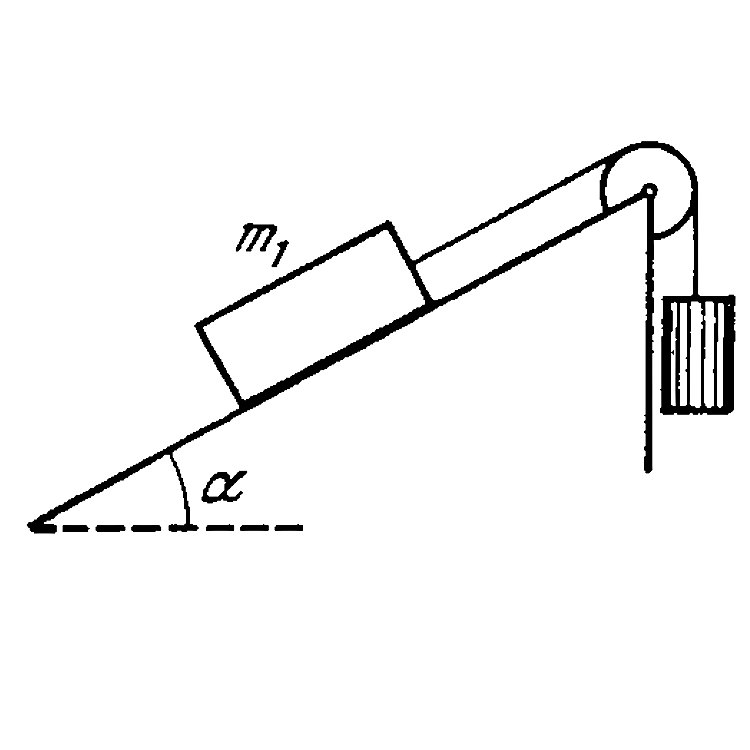
04:23View SolutionThe following parameters of the arrangement of figure are available: the angle α which the inclined plane forms with the horizontal, and the coefficient of friction k between the body m1 and the inclined plane. The masses of the pulley and the threads, as well as the friction in the pulley, are negligible. Assuming both bodies to be motionless at the initial moment, find the mass ratio m2/m1 at which the body m2
(a) starts coming down,
(b) starts going up,
(c) is at rest.
 02:14View Solution
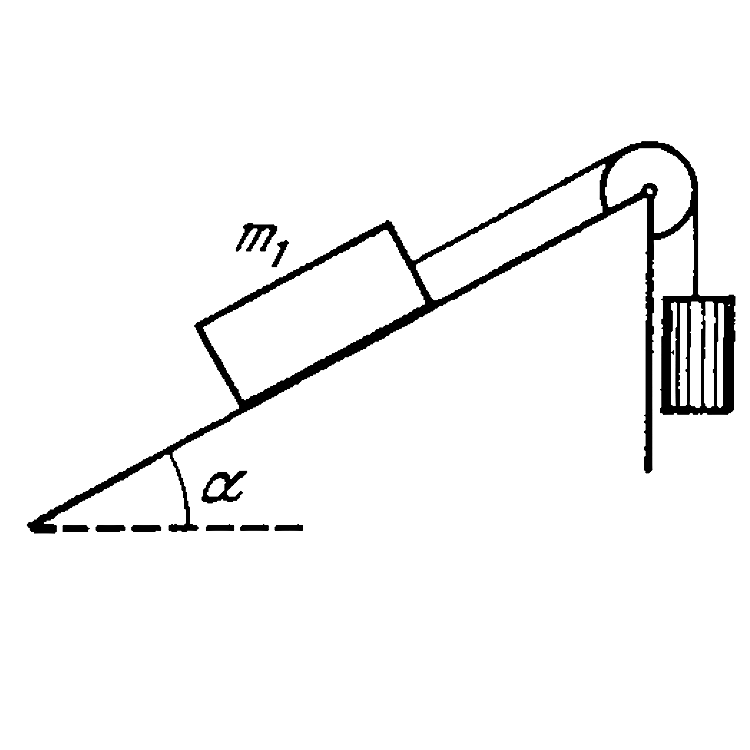
02:14View SolutionThe inclined plane of figure forms an angle α=30∘ with the horizontal. The mass ratio m2/m1=η=2/3. The coefficients of friction between the body m1 and the inclined plane is equal to k=0.10. The masses of the pulley and the threads are negligible. Find the magnitude and the direction of acceleration of the body m2 when the formely stationary system of masses starts moving.
 05:09View Solution
05:09View SolutionIn the arrangement shown in figure the bodies have masses m_0 , m_1 , m_2 , the friction is absent, the masses of the pulleys and the threads are negligible. Find the acceleration of the body m_1 . Look into possible cases.
06:08View SolutionA pulley fixed to the ceiling carries a thread with bodies of masses m_1 and m_2 attached to its ends. The masses of the pulley and the thread are negligible, friction is absent. Find the acceleration w_C of the centre of inertia of this system.
03:08View SolutionTwo bodies of masses m_1 and m_2(
04:06View SolutionIf two masses m_1 and m_2 (m_1 gt m_2) tied to string moving over a frictionless pulley, then acceleration of masses
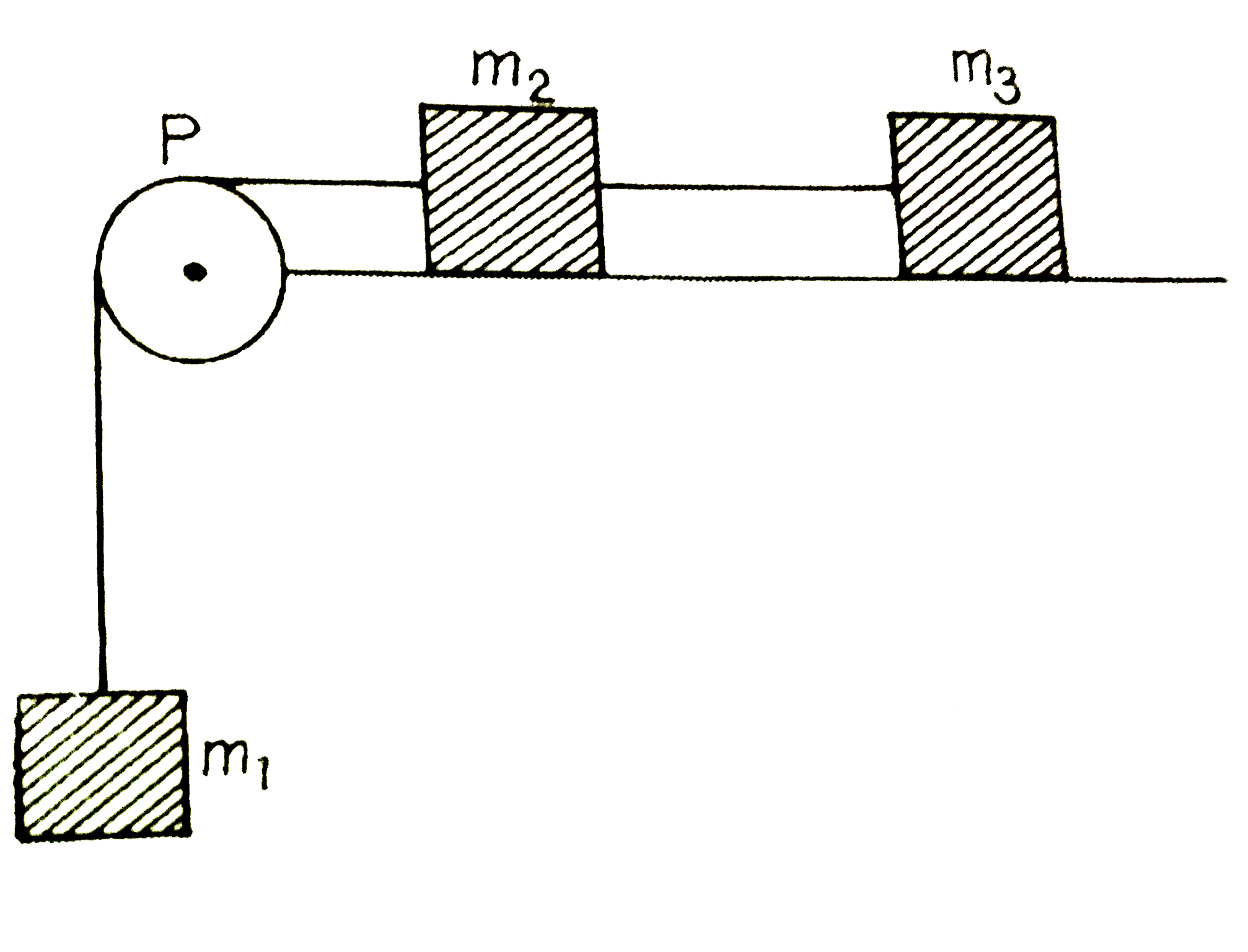
04:17View Solutionयहाँ दर्शाये गये निकाय में तीन पिंड m1,m2 और m3 एक रस्सी से जुड़े है जो एक घिरनी के ऊपर से होकर गुजरती है। m1 मुक्त रूप से लटका है औरm2 तथा m3 एक रुक्ष क्षैतिज मेज पर है, जिसका घर्षण गुणांक =μ है। घिरनी घर्षणरहित है और इसका द्रव्यमान नगण्य है। यदि m1=m2=m3=m है, तो m1 का अधोमुखी (नीचे की ओर) त्वरण होगा:
 05:09View Solution
05:09View SolutionTwo bodies with masses m_1 and m_2 (m_2 gt m) connected by a thread lie on a smooth table. A force Q is first applied to the larger mass and then to the smaller mass. The ratio of tensions in the thread in the two cases will be
02:22View Solution

