Seven identical dominoes (i.., blocks) each of mass m=1kg are to be stacked in three columns and pushed across a frictionless ice rink by a horizontal 10-N force.Assume dominoes do not slip w.r.t. each other. How many dominoes should be in each column, with a minimum of one, (a) to maximize the acceleration of the dominoes, (b) to maximize the force on column C due to column B, (c ) to maximize the net force on column B due to column A and C, and (d) to maximize the force on column B due to column A?

(a) Acceleration of dominoes does not depends upon the number of block as acceleration a=FTotal mass=107ms−2
(b) The maximize force on column C due to column B. The mass of column-C should be maximum. But at least on block should be on one column. Hence 5 blocks should be on colume C and one each on column A and B.
(c) Similarly to maximize the force on cloumn B. Maximum mass should be on column B. Hence column A-one, column-B-five, and column C-one.
(d) To maximize force on column B due to column A only one block should be on column A and remaining six can be placed in any arrangement.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.319videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.413videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.111videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
Similar Questions
Match the column w.r.t column
 View Solution
View SolutionThree identical blocks, each having a mass m are pushed by a force F on the Frictionless table as shown in figure.
What is the net force on the block A?
 View Solution
View SolutionThree identical blocks, each having a mass m are pushed by a force F on the Frictionless table as shown in figure.
What force does B apply on C?
 View Solution
View SolutionMatch the items in column (A) with column (B). Each point in column (A) has minimum one match in column (B) and maximum three matches.
 View Solution
View SolutionThree identical blocks, each having a mass m are pushed by a force F on the Frictionless table as shown in figure.
What force does A apply on B?
 View Solution
View SolutionMatch the item in column (A) with column (B) . Each point in column (A) has minimum one match in colulmn (B) and maximum two matches.
 View Solution
View SolutionThree identical blocks each of mass M are along a frictionless table and a force F is acting as shown. Which of the following statements is false ?
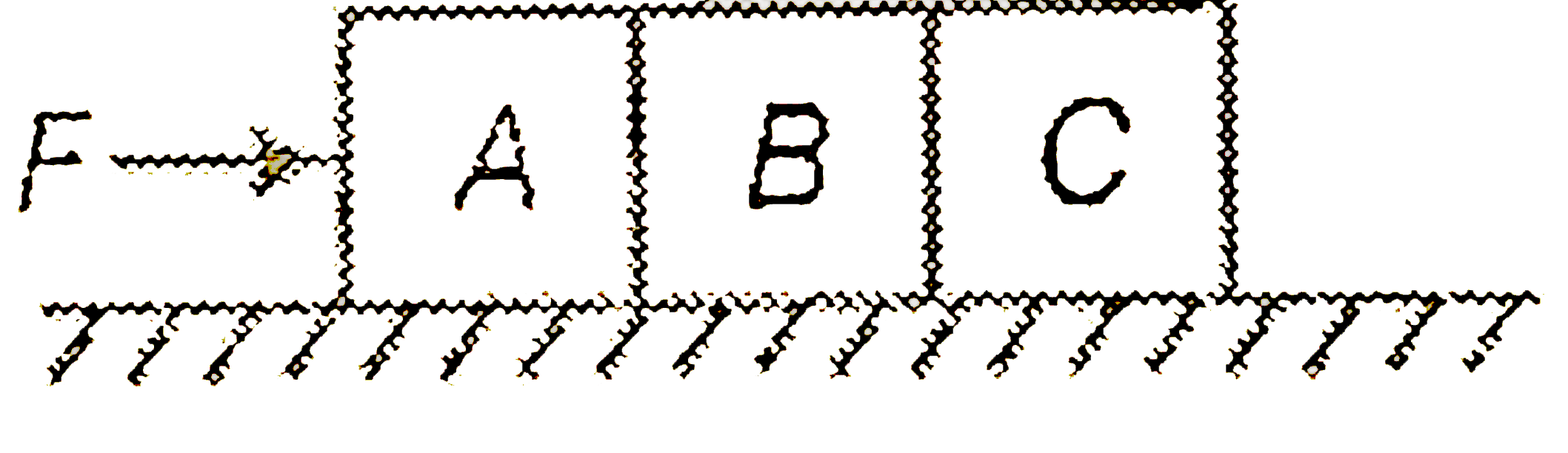 View Solution
View SolutionFor each item in column A, write the letter of the matching item in column B.
 View Solution
View SolutionEntries of Column-I are to be matched with entrices of Column-II. Each entry of Column-I may have the matching with one or more than entries of Column-II
 View Solution
View SolutionEntries of Column-I are to be matched with entrices of Column-II. Each entry of Column-I may have the matching with one or more than entries of Column-II
 View Solution
View Solution

