In the arrangement shown in fig. a wedge of mass m3=3.45kg is placed on a smooth horizontal surface. Small and light pulley is connected on its top edge, as shown. A light, flexible thread passes over the pulley. Two block having mass m1=1.3kgandm2=1.5kg are connected at the ends of the thread.
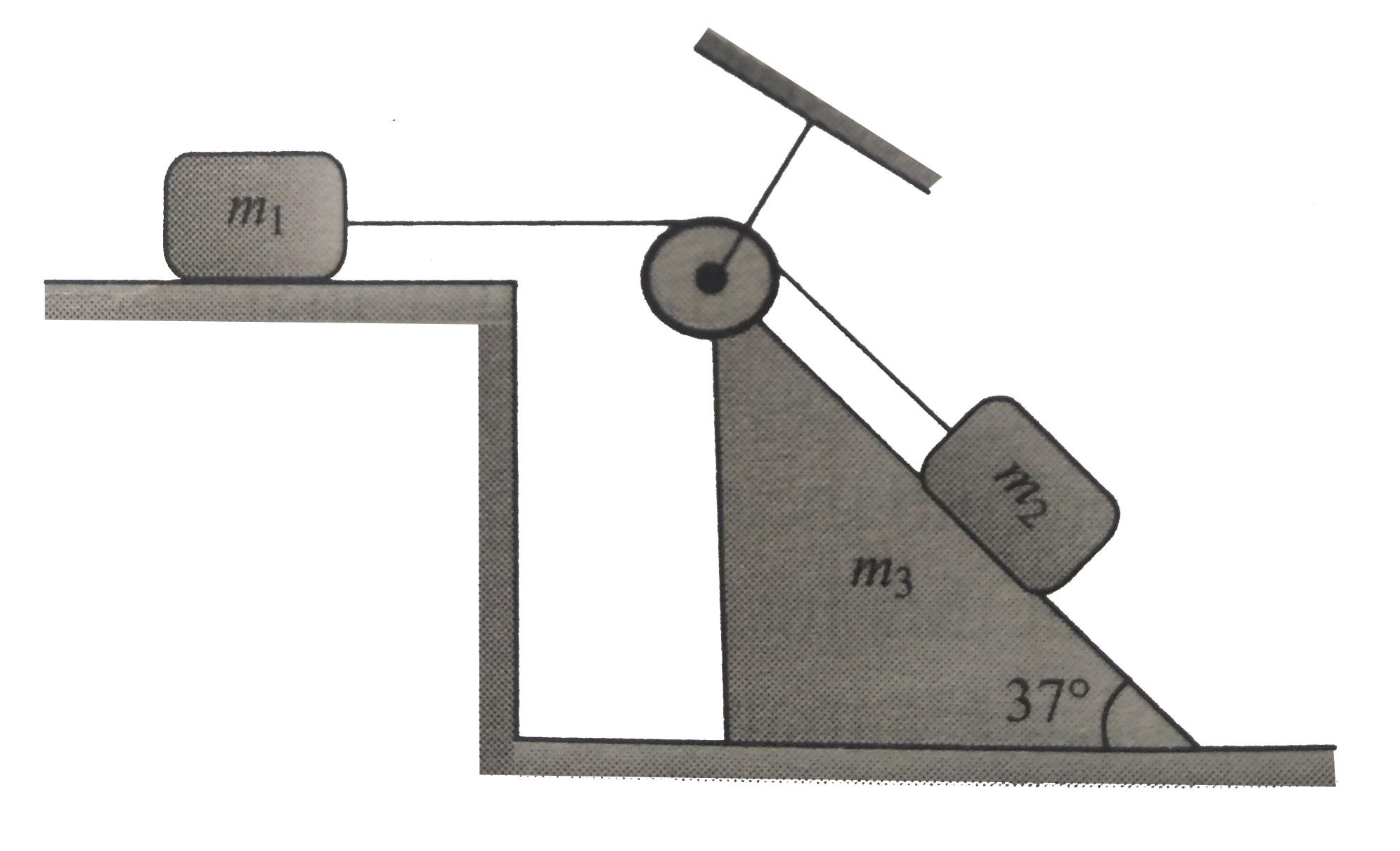
m1 is on smooth horizontal surface and m2 rests on inclined smooth surface of the wedge. the base length of wedge is 2m and inclination is 37∘. m2 is initially near the top edge of the wedge.
If the whole system is released from rest, calculate:
(a) velocity of wedge when m2 reaches its bottom.
(b) velocity of m2 at that instant.
(g=10ms−2).
The correct Answer is:2ms−1;√13ms−1
Let acceleration of m1 be a (rightwards) and that of wedge be b(leftwards). Acceleration of m2 (relative to wedge) becomes (a+b), down the plane. Therefore, resulant acceleration of m2 is vector sum of the two acceleration.
(a) (a+b) down the plane and
(b) b leftwards.
Hence, components of this resultant acceleration are
(a) [(a+b)cos37∘−b]=(4a−b)5 horizontal rightward, and
(b) (a+b)sin37∘=35(a+b) vertically downward.
Considering free body diagrams
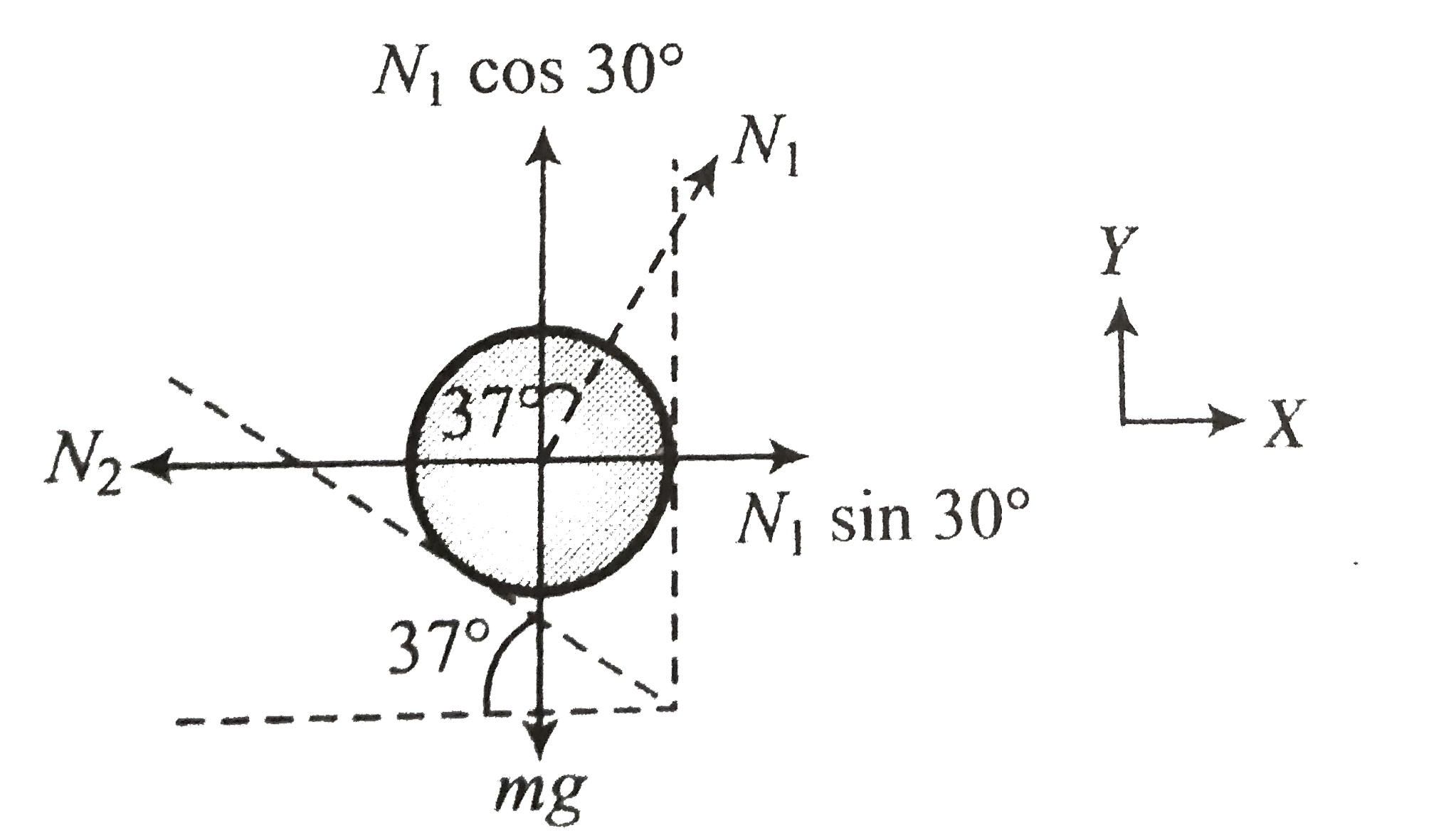
For horizontal force on m1,T=m1a ...(i)
For horizontal force on wedge,
T−Tcos37∘+N2sin37∘=m3b...(ii)
For horizontal force on m2
N2.sin37∘−Tcos37∘=m2(0.8a−0.2) ...(iii)
For vertical force on m2
m2g−N2cos37∘−Tsin37∘=m2(0.6a+0.6b)...(iv)
From above equations , a=3ms−2,b=2ms−2
Since base angle and base length of wedge are 37∘ and 2m respectively, therefore, height of its vertical faces is 2tan37∘=1.5m.
Now considering vertical motion of m2 from top of bottom of the wedge, u=0, acceleration =(0.6a=0.6b)=3ms−2 and displacement = 1.50m.
t=1s
At this instant, horizontal component of velocity of m2 is
v2x=(0.8a−0.2b)t=2ms−1
and vertical component,
v2y=(0.6a+0.6b)t=3ms1
Vertical of m2 is
v2=√v22x+v22y=√13ms−1
Velocity of wedge at this instant = bt=2ms−1.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Single Correct76videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Multiple Correct11videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.413videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
Similar Questions
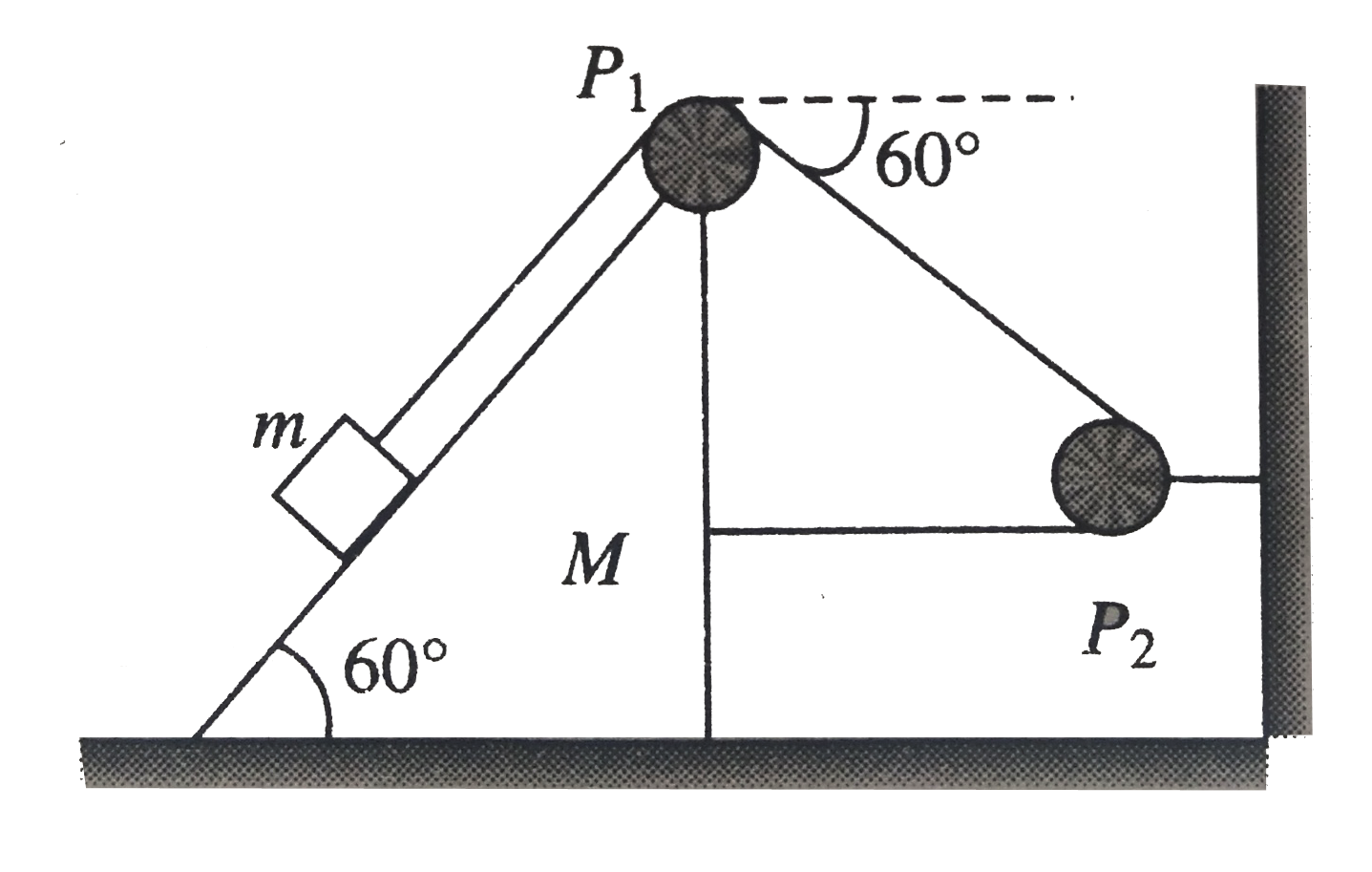
In the arrangement shown in fig. the block of mass m=2kg lies on the wedge of mass M=8kg. The initial acceleration of the wedge, if the surfaces are smooth, is
 View Solution
View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In the arrangement shown in fig. the block of mass m=2kg lies on the wedge of mass M=8kg. The initial acceleration of the wedge, if the surfaces are smooth, is
 A√3g23ms−2B3√3g23ms−2C3g23ms−2Dg23ms−2
A√3g23ms−2B3√3g23ms−2C3g23ms−2Dg23ms−2 - Question 2 - Select One
Two blocks of masses m1=4kg and m2=2kg are connected to the ends of a string which passes over a massless, frictionless pulley. The total downwards thrust on the pulley is nearly
 A27 NB54 NC0.8 NDZero
A27 NB54 NC0.8 NDZero
A block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released
 View Solution
View SolutionTwo blocks of masses m1=4kg and m2=2kg are connected to the ends of a string which passes over a massless, frictionless pulley. The total downwards thrust on the pulley is nearly
 View Solution
View SolutionA block of mass m1=2 kg is kept on a smooth horizontal table. Another block of mass m2=1 kg is connected to m1 by a light inextensible string passing over a smooth pulley as shown in the figure. If the blocks are released, what will be the (a) acceleration of each block (b) tension in the string?
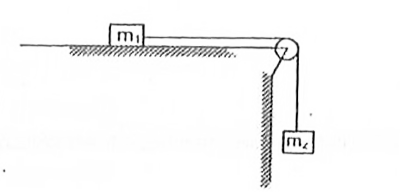 View Solution
View SolutionA block of mass m1=2 kg is kept on a smooth horizontal table. Another block of mass m2=1 kg is connected to m1 by a light inextensible string passing over a smooth pulley as shown in the figure. If the blocks are released, what will be the (a) acceleration of each block (b) tension in the string?
 View Solution
View SolutionThree blocks, placed on smooth horizontal surface are connected by ideal string and a disc shaped pulley of radius r, and mass m. Find the accelerations of the blocks. Masses of the blocks are given as M1=10kg,M2=5kg,M3=2kg,m=2kg.
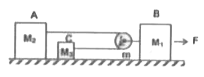 View Solution
View SolutionA block of mass M is placed on a rough horizontal surface. It is connected by means of a light inextensible string passing over a smooth pulley . The other end of string is connected to a block of mass m. There is no friction between vertical surface and block m
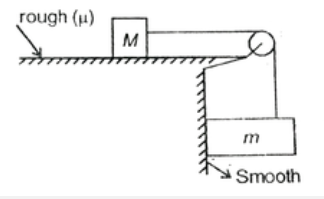
The minimum value of coefficient of friction μ such that system remains at rest , isView Solution

