The system shown in fig is in equilibrium . Masses m1andm2 are 2kg and 8kg, Respectively. Spring constants k1andk2 are 50Nm−1and70Nm−1, respectively. If the compression in second spring is 0.5m. What is the compression in first spring?
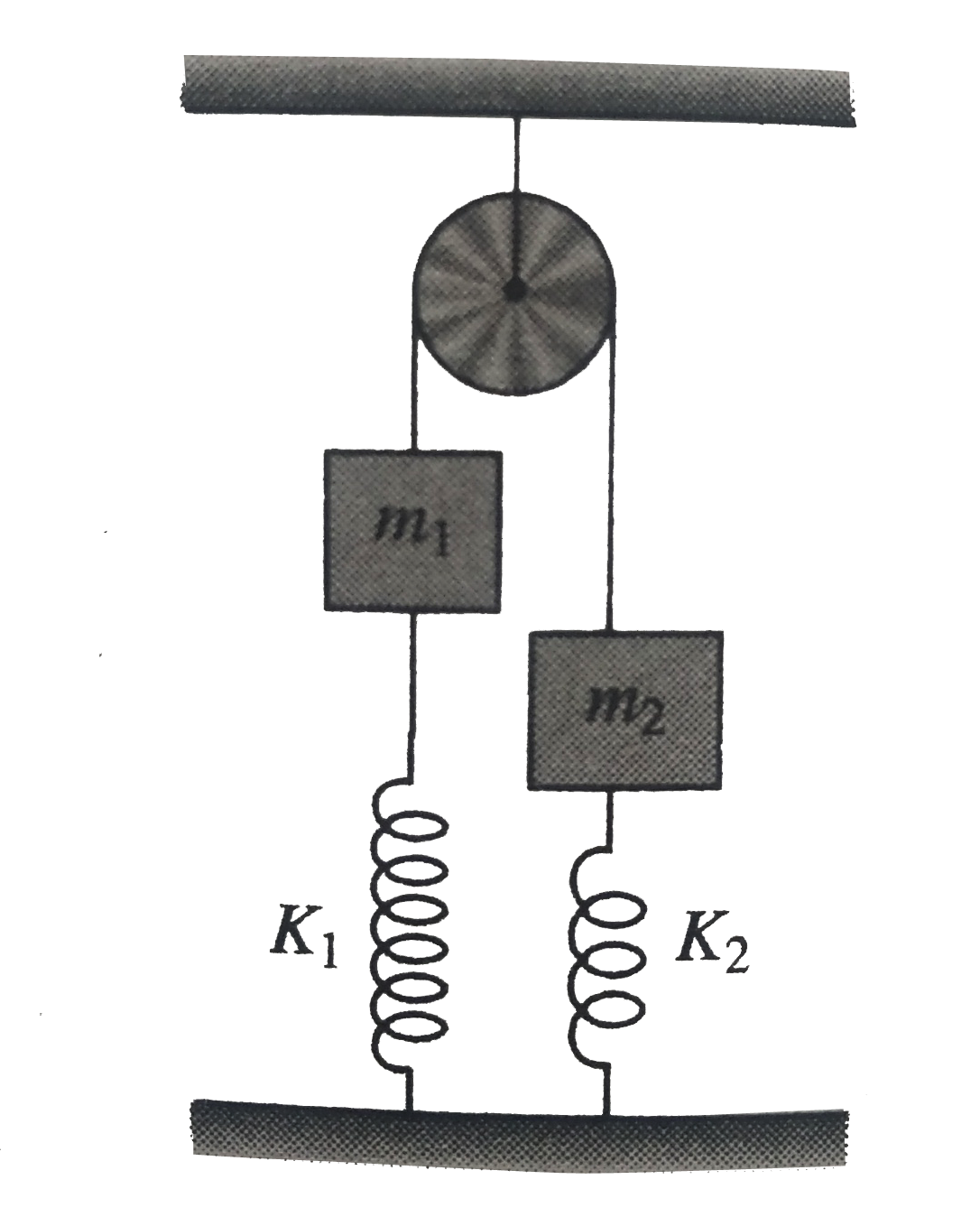
1.3m
−0.5m
0.5m
0.9m
The correct Answer is:B
As the spring have natural length initially, if one spring is compressed, the other must be expanded. Hence, the compression will be negative.
The free-body diagram of m2
T+F2=80N and
F2=70×0.5=35N
∴T=80−35=45N
FBD of m1
T+F1=m1gorF1=−25N
∴X1=−25k1=−2550=−0.5m.
Therefore, compression in first spring is −0.5m.
(negative sign indicates that it is extension)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Multiple Correct11videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Assertion-reasoning15videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Subjective15videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
Similar Questions
Knowledge Check
- Question 1 - Select One or More
The system shown in the figure is in equilibrium. Masses m1&m2 are 2kg and 8 kg respectively. The compression in right spring is 0.5 m. (Both spring have the same natural length) [K1=20N/m,K2=70N/m]. Choose the correct option(s) :
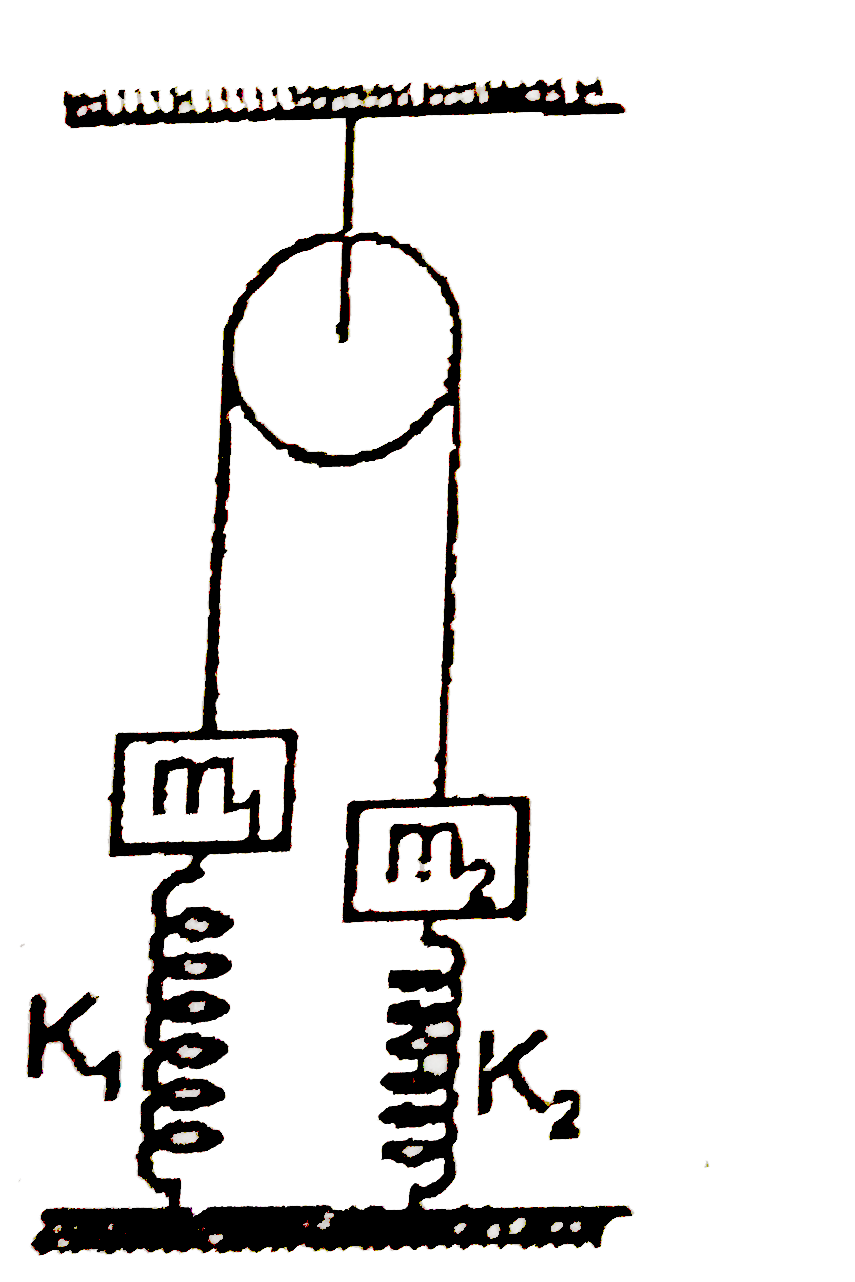 Aelongation in left spring is 0.5mBelongation in left spring is 0.25 mCTension is string is 45 NDJust after left spring is cut m1, has upward acceleration.
Aelongation in left spring is 0.5mBelongation in left spring is 0.25 mCTension is string is 45 NDJust after left spring is cut m1, has upward acceleration. - Question 2 - Select One
Two blocks of masses 1kg and 3kg are moving with velocities 2m/s and 1m/s , respectively , as shown. If the spring constant is 75N/m , the maximum compression of the spring is
 A5cmB2cmC3cmD4cm
A5cmB2cmC3cmD4cm - Question 3 - Select One
A mass M is suspended by two springs of force constants K1andK2 respectively as shown in the diagram. The total elongation (stretch) of the two springs is
 AmgK1+K2Bmg(K1+K2)K1K2CmgK1K2K1+K2DK1+K2K1K2mg
AmgK1+K2Bmg(K1+K2)K1K2CmgK1K2K1+K2DK1+K2K1K2mg
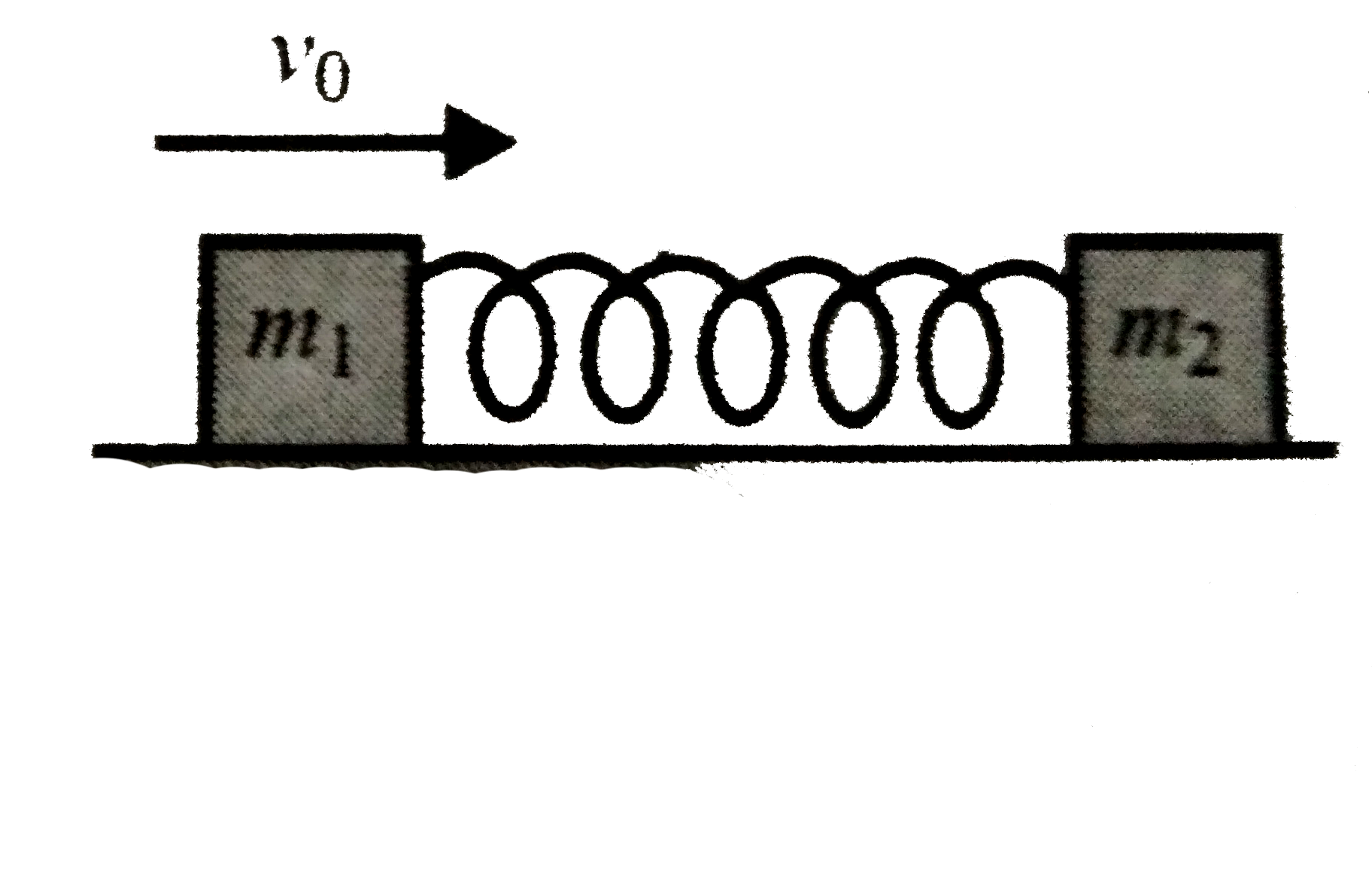
Two smooth blocks of mases m1andm2 attached with an ideal spring of stiffness k and kept on hrozontal surface. If m1 is projected with a horizontal velocity v0. Find the maximum compression of the spring.
 View Solution
View SolutionThe system is in equilibrium and at rest. Now mass m1 is removed from m2. Find the time period and amplituded of resultant motion. Spring constant is K.
 View Solution
View SolutionThe masses in figure slide on a frictionless table. m1 but not m2, is fastened to the spring. If now m1 and m2 are pushed to the left , so that the spring is compressed a distance d, what will be the amplitude of the oscillation of m1 after the spring system is released ?
 View Solution
View Solution
In an elevator a system is arranged as shown in figure. Initially elevator is at rest and the system is in equilibrium with middle spring unstretched. When the elevator accelerated upwards, it was found that for the new equilibrium position (with respect to lift), the further extension i the top spring is 1.5 times that of the further compression in the bottom spring, irrespective of the value of acceleration
(a) Find the value of m1m2 in terms of spring constants for this happen.
(b) if k1=k2=k3=500Nm and m1=2 kg and acceleration of the elevator is 2.5ms2, find the tension in the middle spring in the final equilibrium with respect to lift.View SolutionA spring of length 'l' has spring constant 'k' is cut into two parts of length l1 and l2. If their respective spring constahnt are K1 and k2, then K1K2 is:
View Solution



