Seven pulleys are connected with the help of three light string as shown in fig.Consider P3,P4,P5 as light pulleys and pulleys P6 and P7 have masses m each. For this arrangement, mark the correct statement(s)
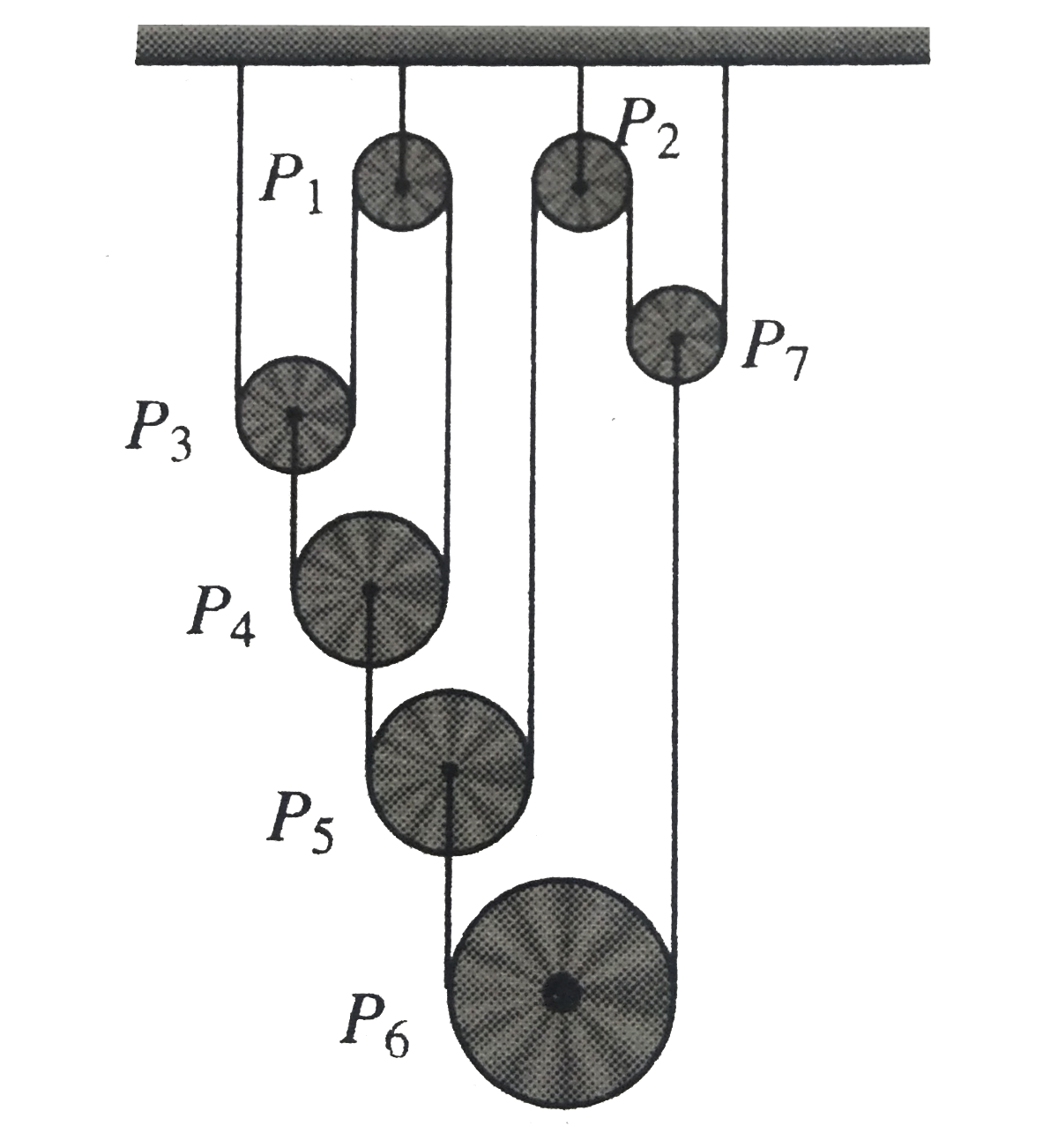
Tension in the string connecting P1,P3andP4 is zero.
Tension in the string connecting P1,P3andP4 is mg/3
Tension in all the three strings are same and equal to zero.
Acceleration of P6 is g downwards and that of P7 is g upwards.
The correct Answer is:A, C
First of all, draw FBD of P3. Let tensions, in three strings be T1,T2 and T3, respectively.
2T1−T1=0×a⇒T1=0
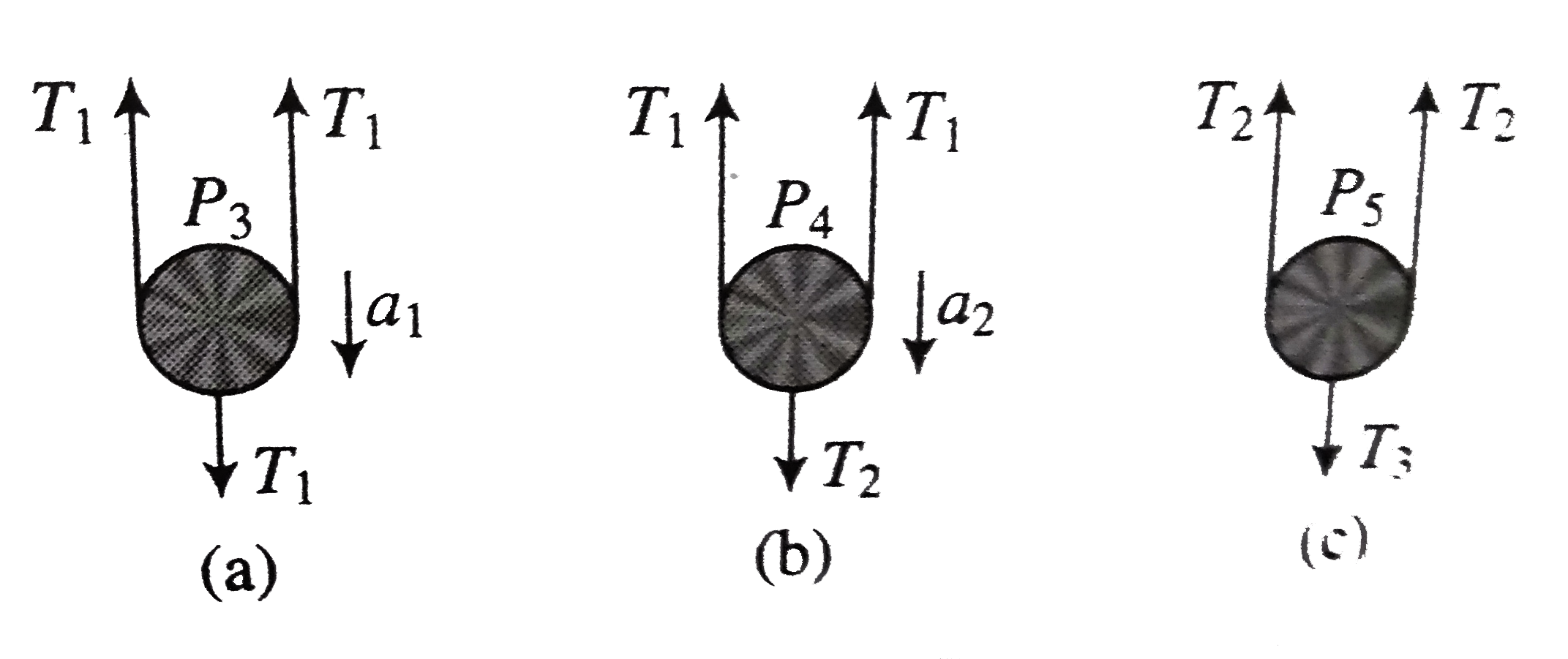
Now draw FBD of P4andP5 .
2T1−T2=0⇒T2=0
2T2−T3=0⇒T2=T3=0
So forces acting of P6andP7 will be that of gravity and they will be in free fall.Hence acceleration of each of them will be g down wards.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Assertion-reasoning15videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Linked Comperhension46videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Single Correct76videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
Similar Questions
The force exerted by the ideal string on the ideal pulley P shown in the figure is
 View Solution
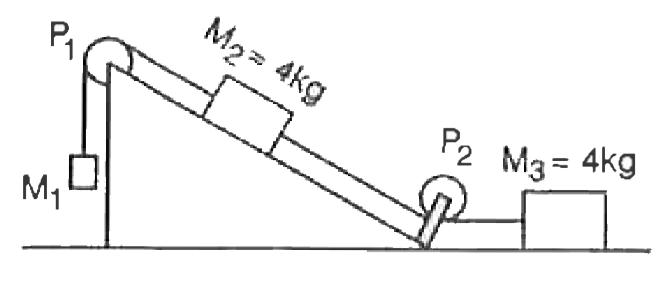
View SolutionMasses M1,M2andM3 are connected by string of negligible mass which pass over massless and frictionless pulleys P1andP2 as shown in figure 7.15. The masses move such that the string between P1andP2 is parallel to the incline and the portion of the string between P2andM3 is horizontal. The masses M2andM3 are 4.0 kg each and the coefficient of kinetic friction between the masses and the surfces is 0.25. The inclined plane makes an angle of 37∘ with the horizontal. If the mass M1moves downwards with a uniform velocity, find (i) the mass of M1, (ii) the tension in the horizontal portion. (g=9.8ms−2,sin37∘=35)
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The acceleration of the block B in fig. Assuming the surfaces and the pulley P1 and P2 are all smooth, is
 AF4mB3F13mCF2mD3F17m
AF4mB3F13mCF2mD3F17m - Question 2 - Select One or More
Two masses m and M(m<M) are joined by a light string passing over a smooth and light pulley (as shown)
 Athe acceleration of each mass is (M−mM+m)gBthe tension in the string connecting masses is (2MmM+m)gCthe thrust acting on the pulley is (4MmM+m)gDNone of the above
Athe acceleration of each mass is (M−mM+m)gBthe tension in the string connecting masses is (2MmM+m)gCthe thrust acting on the pulley is (4MmM+m)gDNone of the above - Question 3 - Select One
In the pulley system shown in fifure the movable pullet=ys A,B and C are of mass 1 kg each D and E are fixed pulleys are light and inexensible.
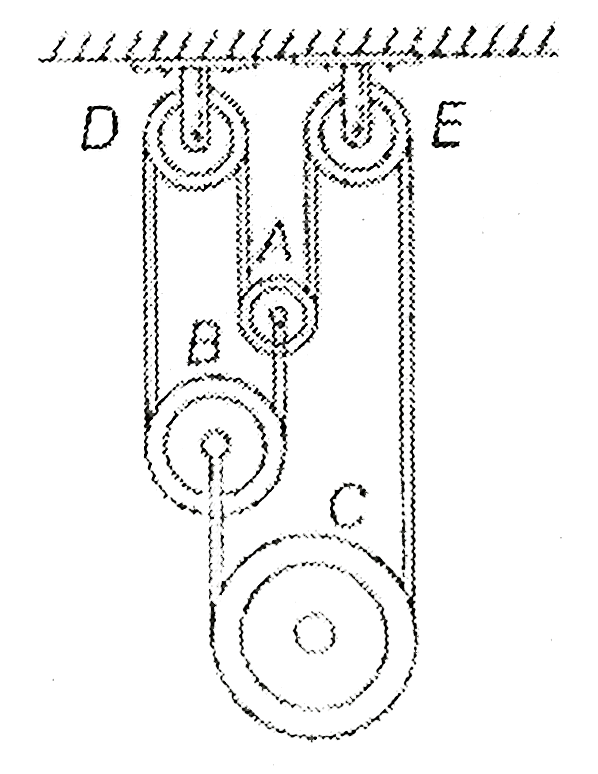
Choose the correct alternative (s).ATension in the string is 6.5 NBAcceleration of pulley A is g/3 downwardCAcceleration of pulley B is g.\6 upwardDAcceleration of pulley C is g/3 upward
find the acceleration of the block of mass M in the situation shown in figure. All the surfaces are frictionless and the pulleys and the string are light.
 View Solution
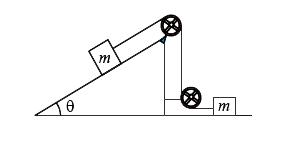
View SolutionTwo blocks each of mass m are connected over two light and frictionless pulleys and a fixed wedge by a light string as shown in figure. The tension in the string is :
 View Solution
View SolutionTwo masses m1 and m2 are connected by means of a light string,that passes over a light pulley as shown in the figure.If m1=2kg and m2=5kg and a vertical force F is applied on the pulley then find the accelerations of the masses and that of the pulley when the force is F=70N
View SolutionMasses M1,M2andM3 are connected by string of negligible mass which pass over massless and frictionless pulleys P1andP2 as shown in figure 7.15. The masses move such that the string between P1andP2 is parallel to the incline and the portion of the string between P2andM3 is horizontal. The masses M2andM3 are 4.0 kg each and the coefficient of kinetic friction between the masses and the surfces is 0.25. The inclined plane makes an angle of 37∘ with the horizontal. If the mass M1moves downwards with a uniform velocity, find (i) the mass of M1, (ii) the tension in the horizontal portion. (g=9.8ms−2,sin37∘=35)
 View Solution
View SolutionAn arrangement of the masses and pulleys is shown in the figure. Strings connecting masses A and B with pulley are horizontal and all pulleys and strings are light. Friction coefficient between the surface and the block B is 0.2 and between block A and B is 0.7. The system is released from rest. (use g=10m/s2)
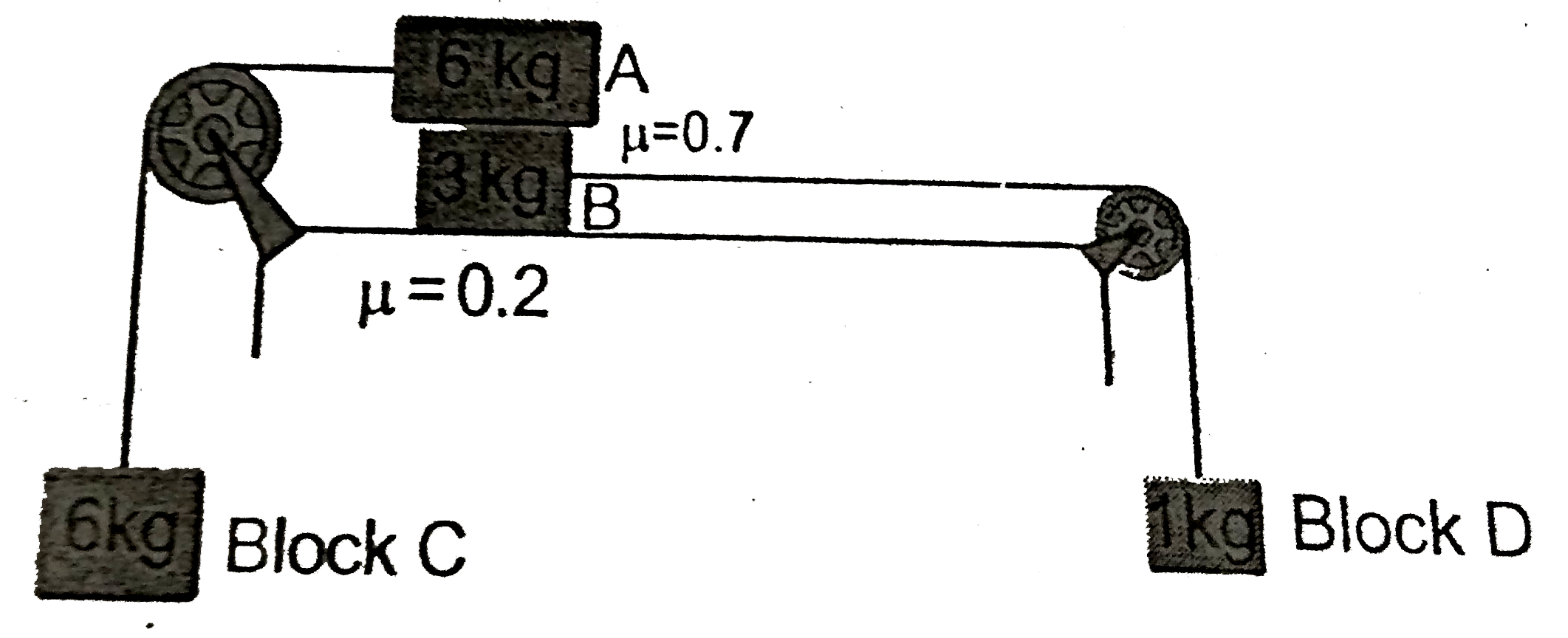 View Solution
View Solution

