Two block M and and m are arranged as shows in figure . If M=50kg then determine the minimum and maximum value of mass of block the heavy block M stationary

Since the angle of inclination of the plane is more than the angle of repose i, e 37∘>tan−10.5 or tan37∘>0.5 therefore the block M has a tendency to slide down in order to tension in of stationary the neccessury force is applied by the tension in the string
If the block M also has the tendency to side down the friction will act in up the plane
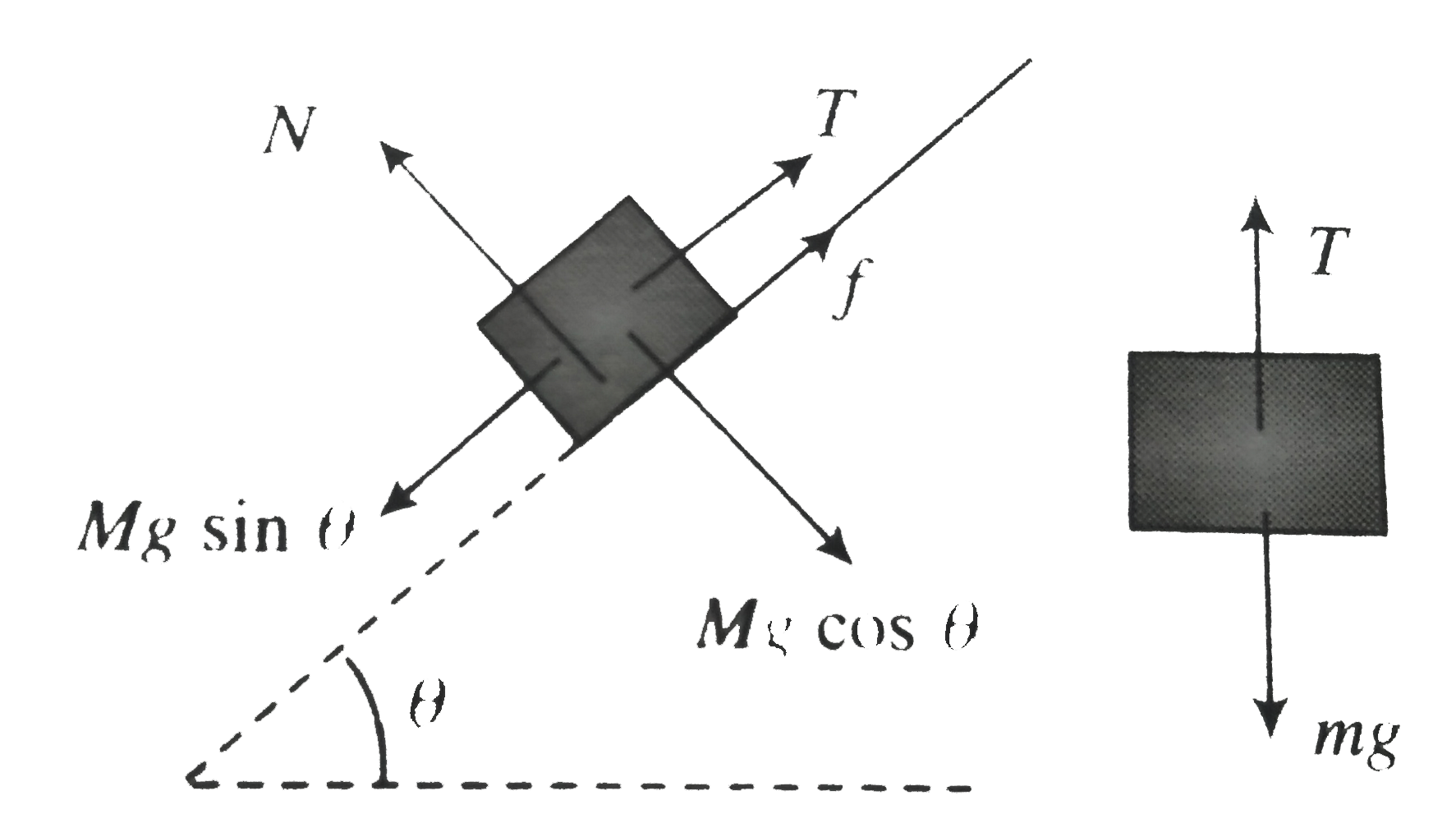
For Equation of M:f=Mgsinθ−T ...(i)
For Equation of m:T=Mg...(ii) from(i) and (ii) f=Mgsinθ−mg ....(iii)
for friction to be staticf<fmax
Mgsinθ−mg+μs(Mgsinθ)
⇒Msinθ−μscosθ<m
Hence , m>M(sinθ−μscosθ) ...(iv)
or m>50(35−35×45)⇒m>6
Hence minimum value of mass mmin=6kg
If block M has the tendency in slide down the friction with act in downward direction by the relation we get the maximum value of m This static of as can be obtation by simply substing (μs) is place of μs in fig (iv) finaly we will get the relation
m>M(sinθ−(−μs)cosθ)
⇒m>M(sinθ+μs)cosθ)
m<50(35+35×45)⇒m<54kg
Hence the maximum value of mass mmax=54kg
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Solved Examples12videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.125videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer5videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
Similar Questions
Knowledge Check
- Question 1 - Select One

Two blocks of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is :Am2gm1+m2Bm1gm1+m2C4m2g−m1gm1+m2Dm2gm1+4m2 - Question 2 - Select One
Two block of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is:
 Am2gm1+m2Bm1gm1+m2C4m2g−m1gm1+m2Dm2gm1+4m2
Am2gm1+m2Bm1gm1+m2C4m2g−m1gm1+m2Dm2gm1+4m2 - Question 3 - Select One
Two blocks A and B are connected by as string as shown in figure. Friction coefficient of the incline plane and block is 0.5. The mass of the block A is 5kg. If minimum & maximum values of masses of the block B for which the block remains in equilibrium are m1 & m2 then find value of (m2−m1).
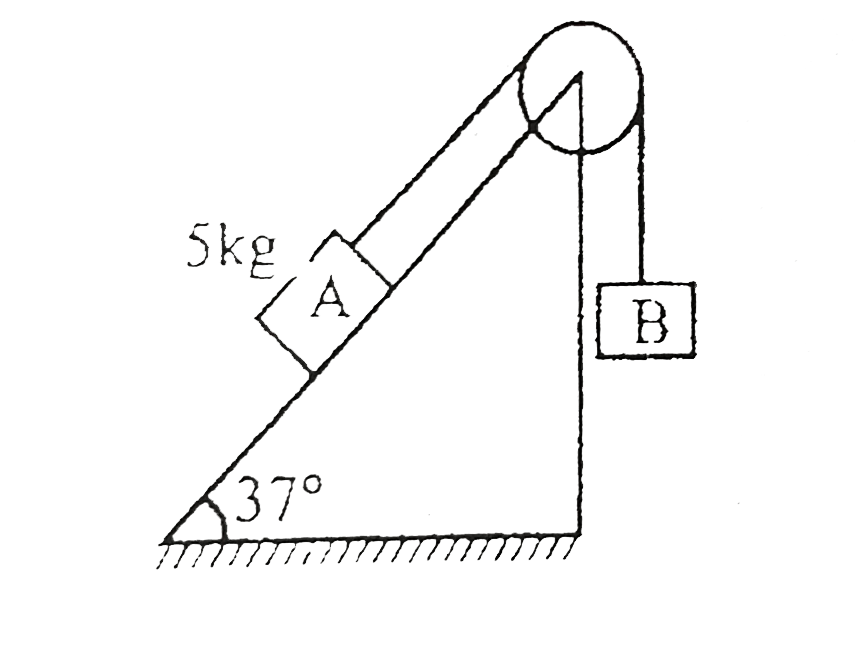 A4B6C3D2
A4B6C3D2
Two blocks A and B are arranged as shown in figure.The pulleys are light and frictionless.The strings are light and inextensible.If the acceleration of the block B is 3ms2 ,then the acceleration of the block A is __________ms2
View SolutionA block of mass m collides with another block of mass 3m completely inelastically as shown in figure. What is the maximum value of v( in m/s) for which the block B does not move. Assume that initially spring is in natural length and blocks A and B are at rest. (K/m=100S.I.unit )
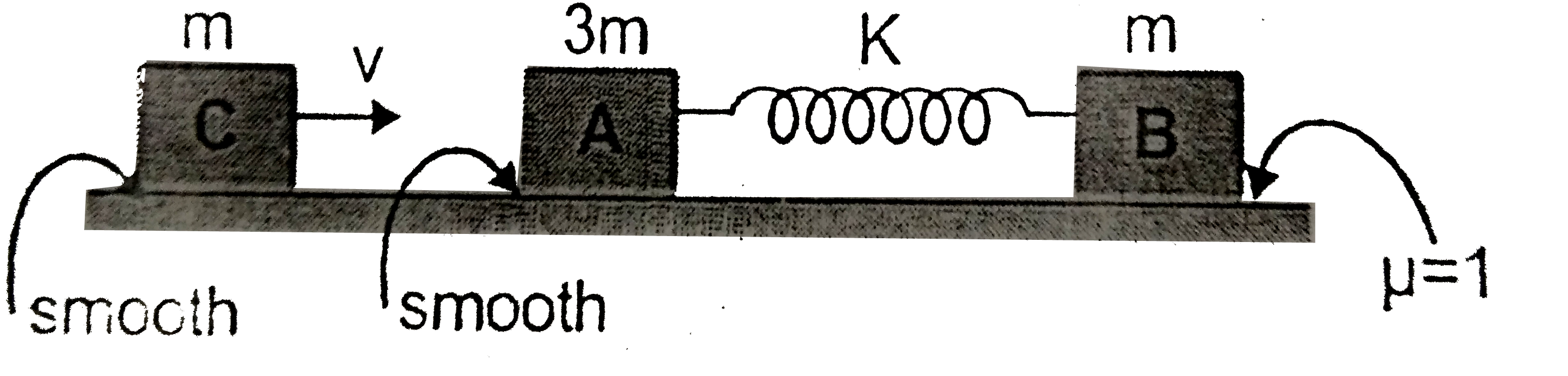 View Solution
View SolutionTwo blocks of masses 2m and m are in equilibrium a shown in the figure. Now the string between the blocks is suddenly broken. The accelarations of the blocks A and B respectively, at that instant are
 View Solution
View SolutionA uniform cubical block of mass M is attached to a pulley. One end of a string, passing over the pulley is fixed to a light pole while is fixed on the bigger block and its another end is attached to a block of mass m as shown in figure. The maximum value of the mass m so that the block does not topple is : (string and pulley are ideal)
 View Solution
View SolutionA block of mass m resting on a wedge of angle θ as shown in the figure. The wedge is given an acceleration a. What is the minimum value of a so that the mass m falls freely ?
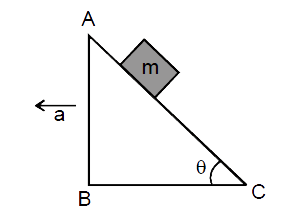 View Solution
View Solution



