A vertical rod of mass m is kept on a wedge of mass M. If a horizontal force F acts on the wedge and the rod is constrained to move vertically, after releasing the rod-wedge system, (a) find their speeds when the wedge moves through a distance x. (b) What is the power delivered by the rod on the wedge aftre a time t measured from the instant of release?
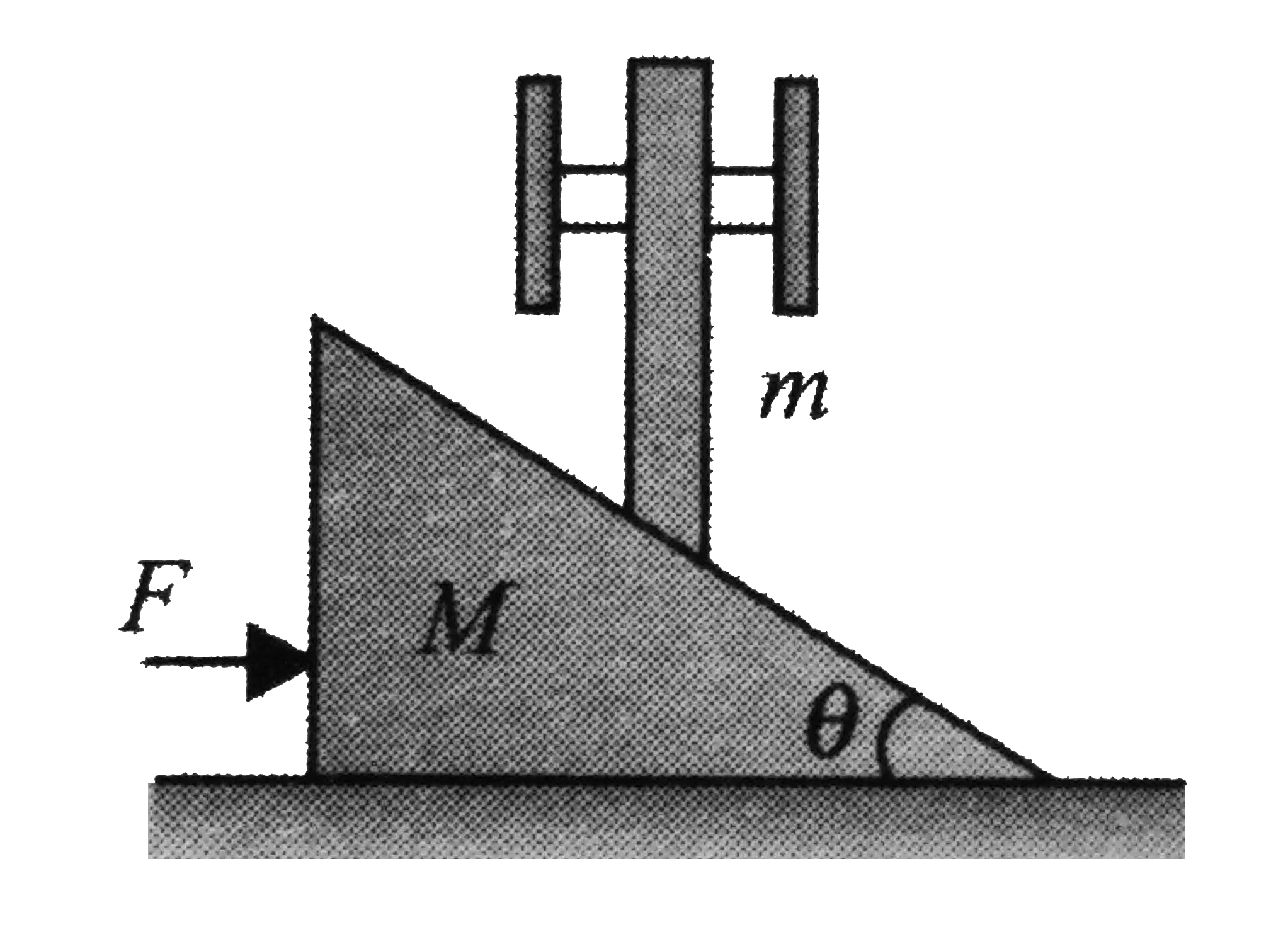
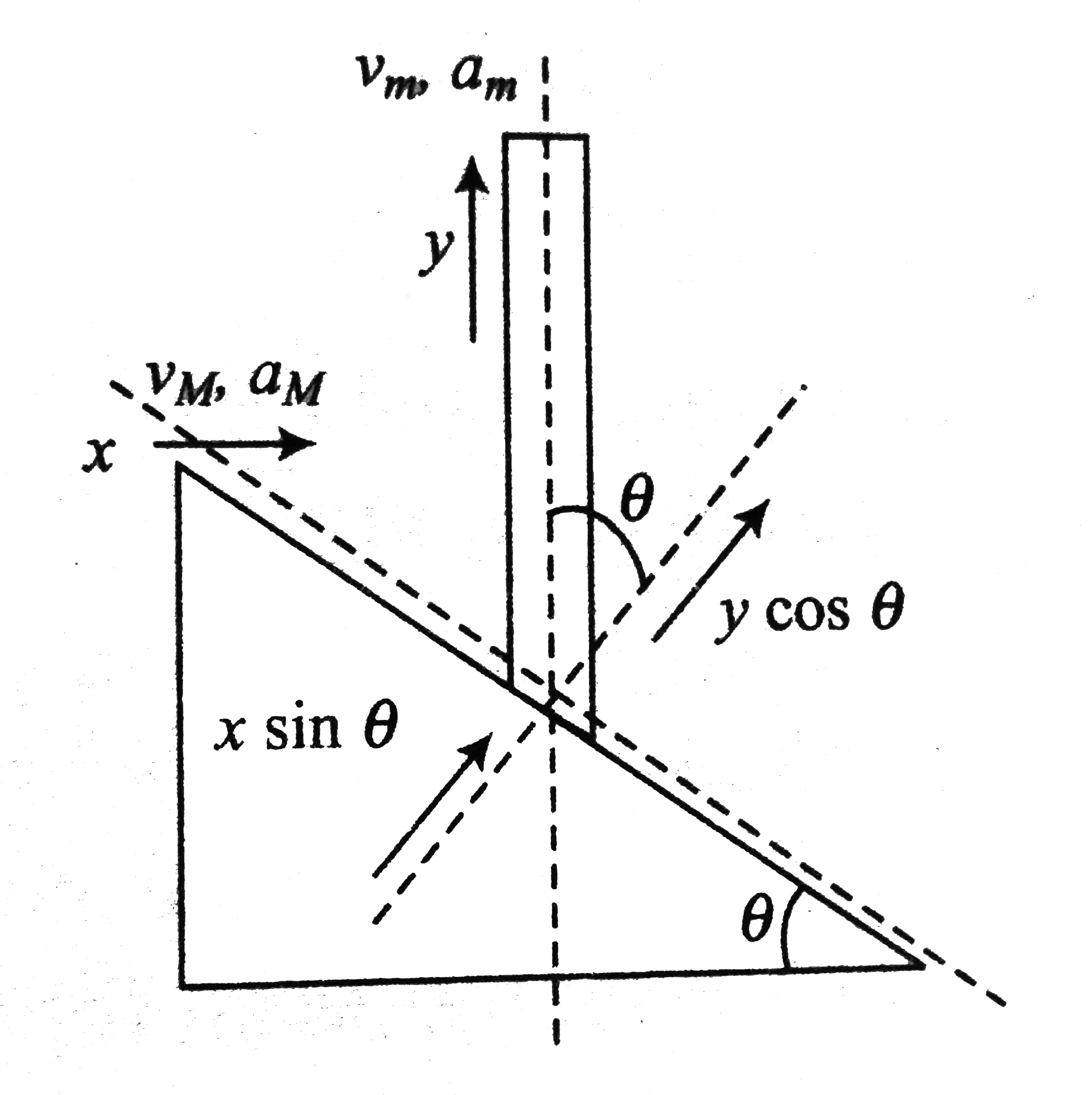
a. Let the displacement of rod is y when wedge moves a distance x,
xsinθ=ycosθ⇒x=ytanθ
Also vm=vMtanθ and am=aMtanθ
Apply work-energy theorem:
W=ΔKE
⇒Fx−mgy=12Mv2M+12mv2m
⇒(F−mgtanθ)x=12Mv2M+12mv2Mtan2θ
⇒vM=√2[F−mgtanθ]xM+mtan2θ
and
vm=vMtanθ=√2[F−mgtanθ]xMcot2θ+m
b. From FBD of wedge and rod,
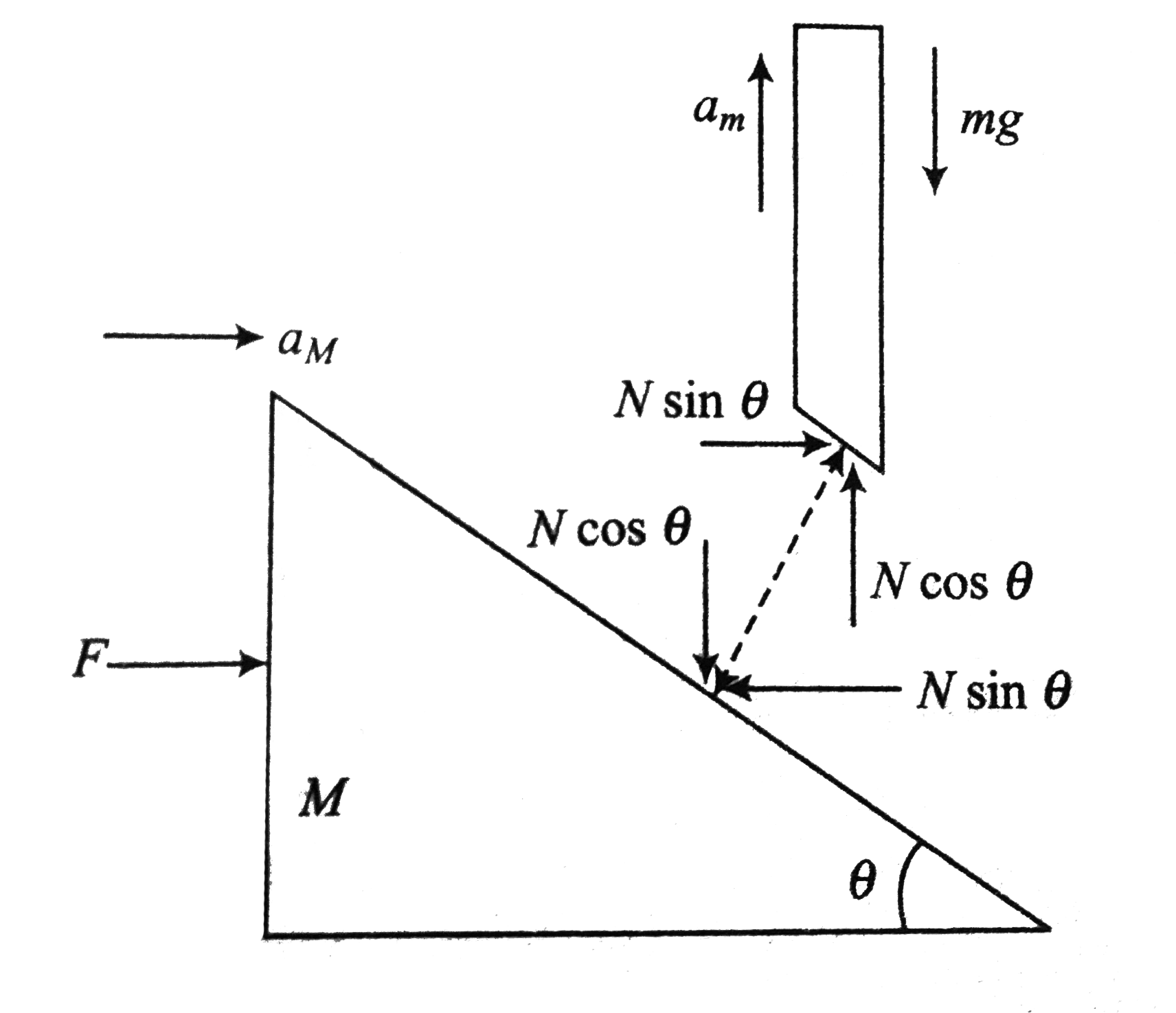
F−Nsinθ=MaM (ii)
Ncosθ−mg=mam (ii)
From (i), and (ii)
aM=F−mgtanθM+mtan2θ
N=(Ftanθ+Mg)m(M+mtan2θ)cosθ
Velocity of M after time t,
vM=aMt
Power given by rod by wedge
P=−(Nsinθ)vM
=−NaMsinθt
=−mtanθ[Ftanθ+Mg][F−mgtanθ][M+mtan2θ]2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.125videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.225videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (integer)4videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
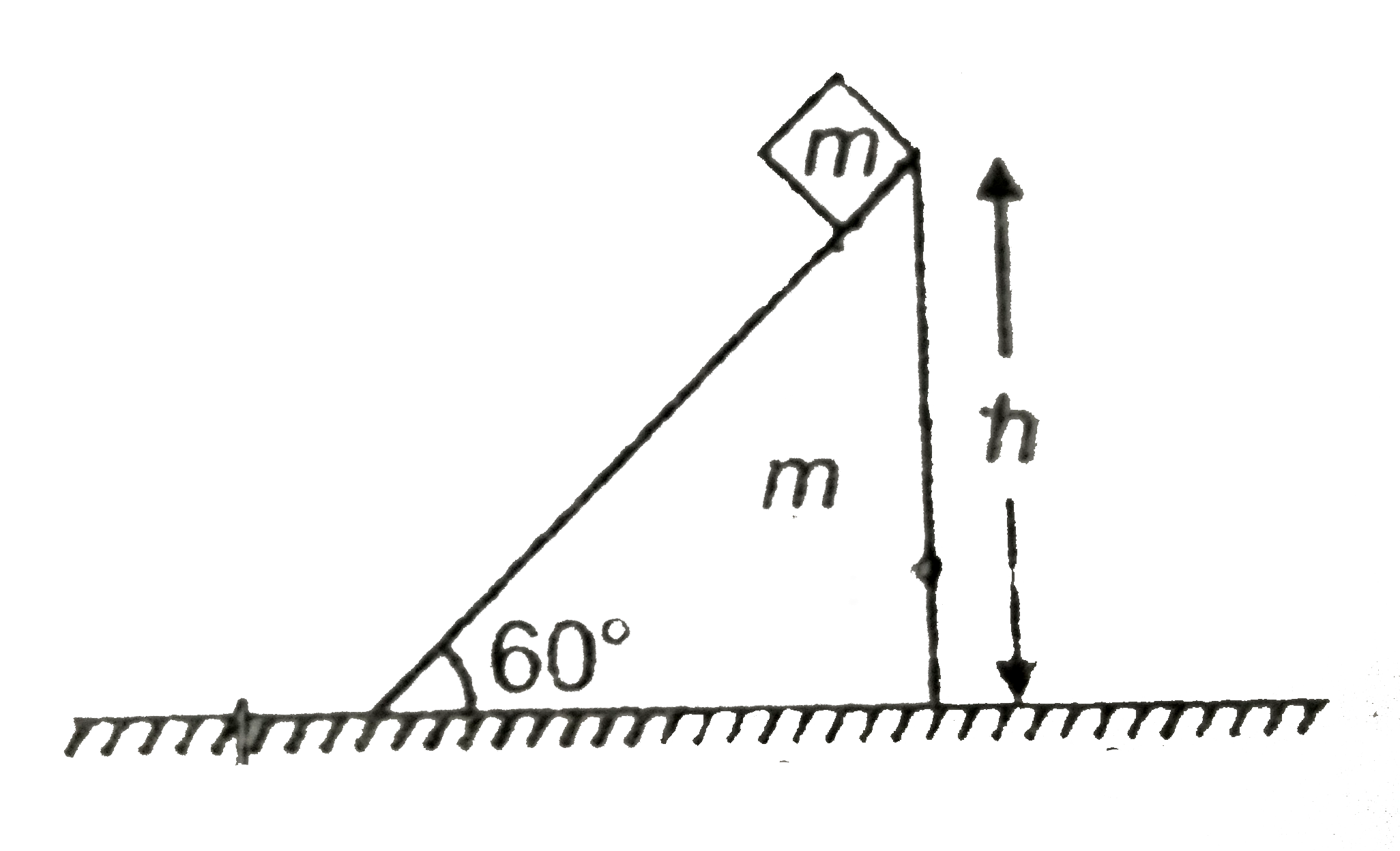
A block of mass m is released from a wedge of mass m as shown in figure . Find the time taken by the block to reach the end of the wedge.
 View Solution
View SolutionA block of mass m, is kept on a wedge of mass M, as shown in figure such that mass m remains stationary w.r.t. wedge. The magnitude of force P is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A smooth vertical rod is released from rest such that it is constrained to move vertically on a smooth wedge (θ=45∘). When the wedge moves through a distance x, the speed of the rod is :
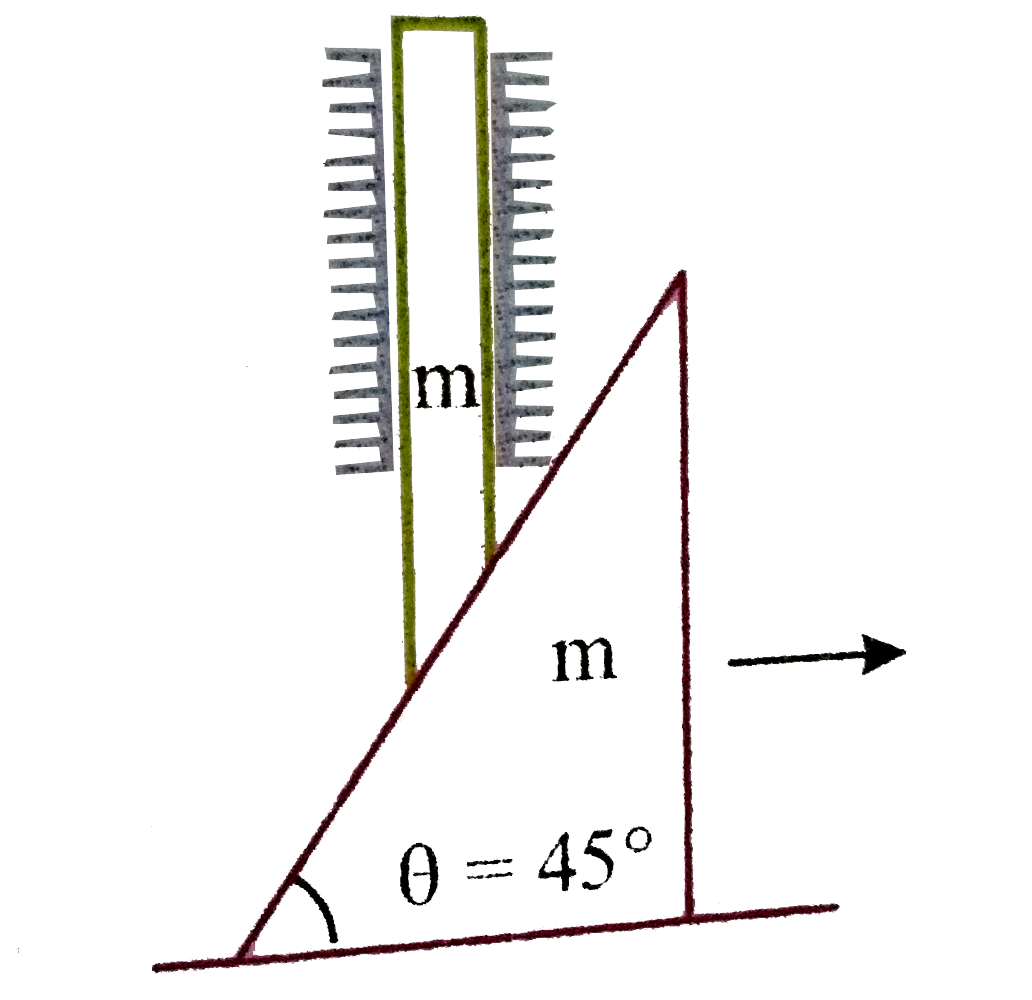 . A√2gxB√gx2C√gxDnone of these
. A√2gxB√gx2C√gxDnone of these - Question 2 - Select One
A wedge of mass M resting on a horizontal frictionless surface is acted upon by a force F in the horizontal direction as shown in figure. Find the net horizontal force acting on the shaded portion of the wedge.
 AFBF3CF6Dzero
AFBF3CF6Dzero - Question 3 - Select One
A block of mass m is placed on a smooth wedge of inclination θ & mass M. The whole system is slip on the wedge. Then the normal reaction on the wedge acting from the ground :
A(M+m)gB(M+msinθ)gCMgD(M+msinθM+m)gcosθ
A block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released
 View Solution
View SolutionA rod of mass m is supported on a wedge of mass M shown in fig. Find the accelerations of rod a and wedge A in the arrangment. The friction between all contact surfaces in negligible.
 View Solution
View SolutionA block of mass m is placed on wedge of mass M (Fig.). Find the accelerations of the block and the wedge in the reference system fixed to the table, and the reaction. Friction is to be neglected.
Analyse the limiting case when the wedge remains stationary.
 View Solution
View SolutionA ball of mass m is released from A inside a smooth wedge of mass m as shown in figure. What is the speed of the wedge when the ball reaches point B?
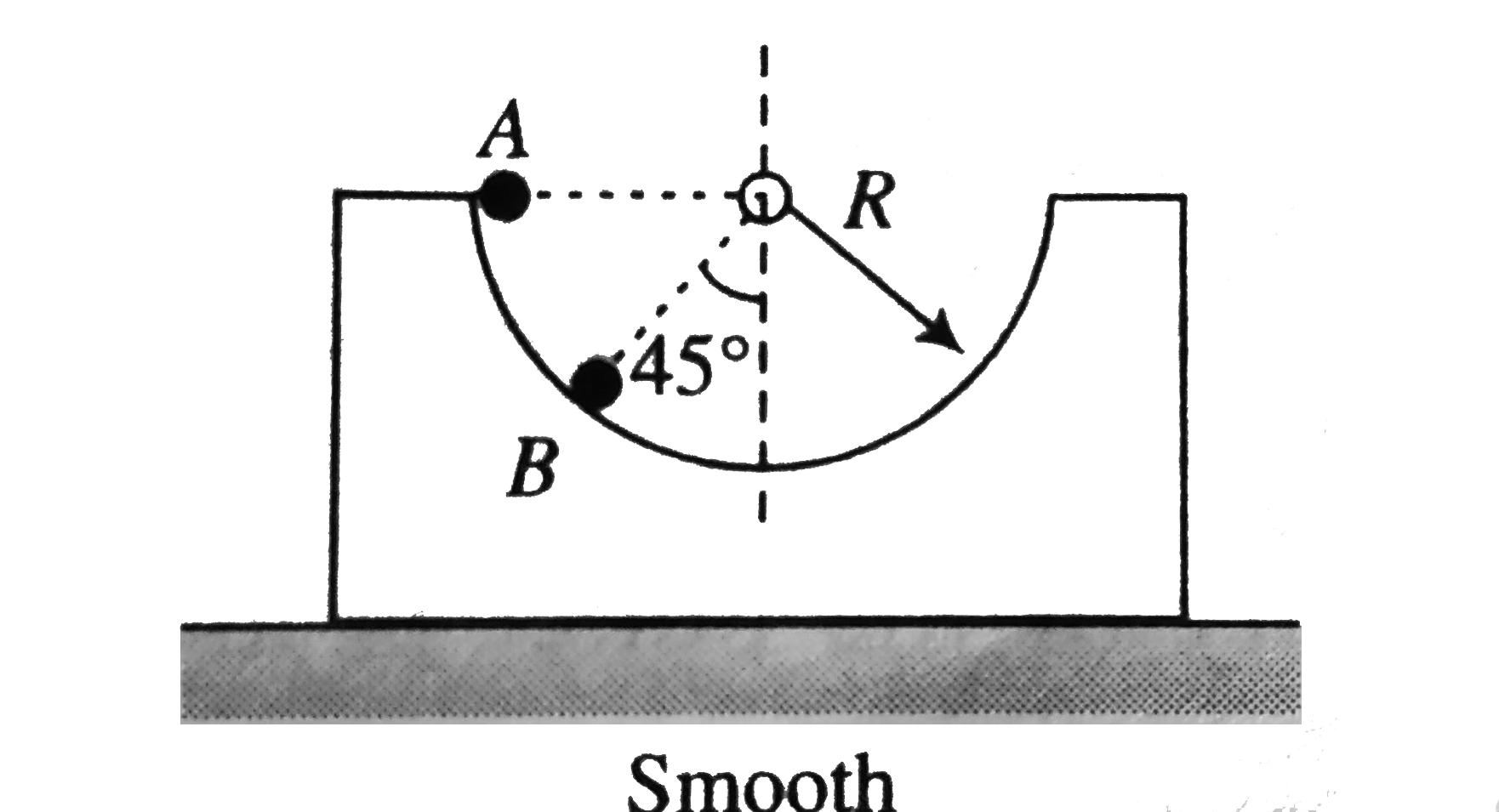 View Solution
View SolutionA cube of mass m is placed on top of a wedge of mass 2m, as shown in figure. There is no friction between the cube and the wedge. The minimum co - efficient of friction between the wedge and the horizontal surface, so that the wedge does not move is
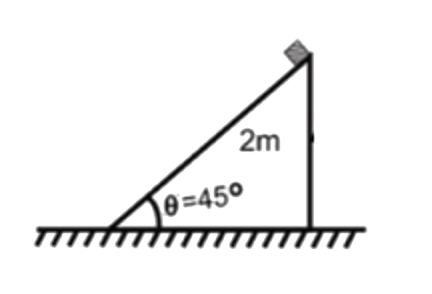 View Solution
View Solution

