A block A of mass m=5kg is attached with a spring having force constant K=2000Nm−1. The other end of the spring is fixed to a rough plane, inclined at 37∘ with horizontal and having coefficient of friction m=0.25. Block A is gently placed on the plane such that the spring has no tension. Then block A is released slowly. Calculate elongation of the spring when equilibrium is achieved. Now an inextensible thread is connected with block A and passes below pulley C and over pulley D, as shown in figure. Other end of the thread is connected with another block B of mass 3kg. Block B is resting over a table and thread is loose. If the table collapse suddenly and B falls freely through 80/9cm, the thread becomes taut, calculate combined speed of blocks at that instant, and maximum elongation of spring in the process of motion. (g=10ms−2).
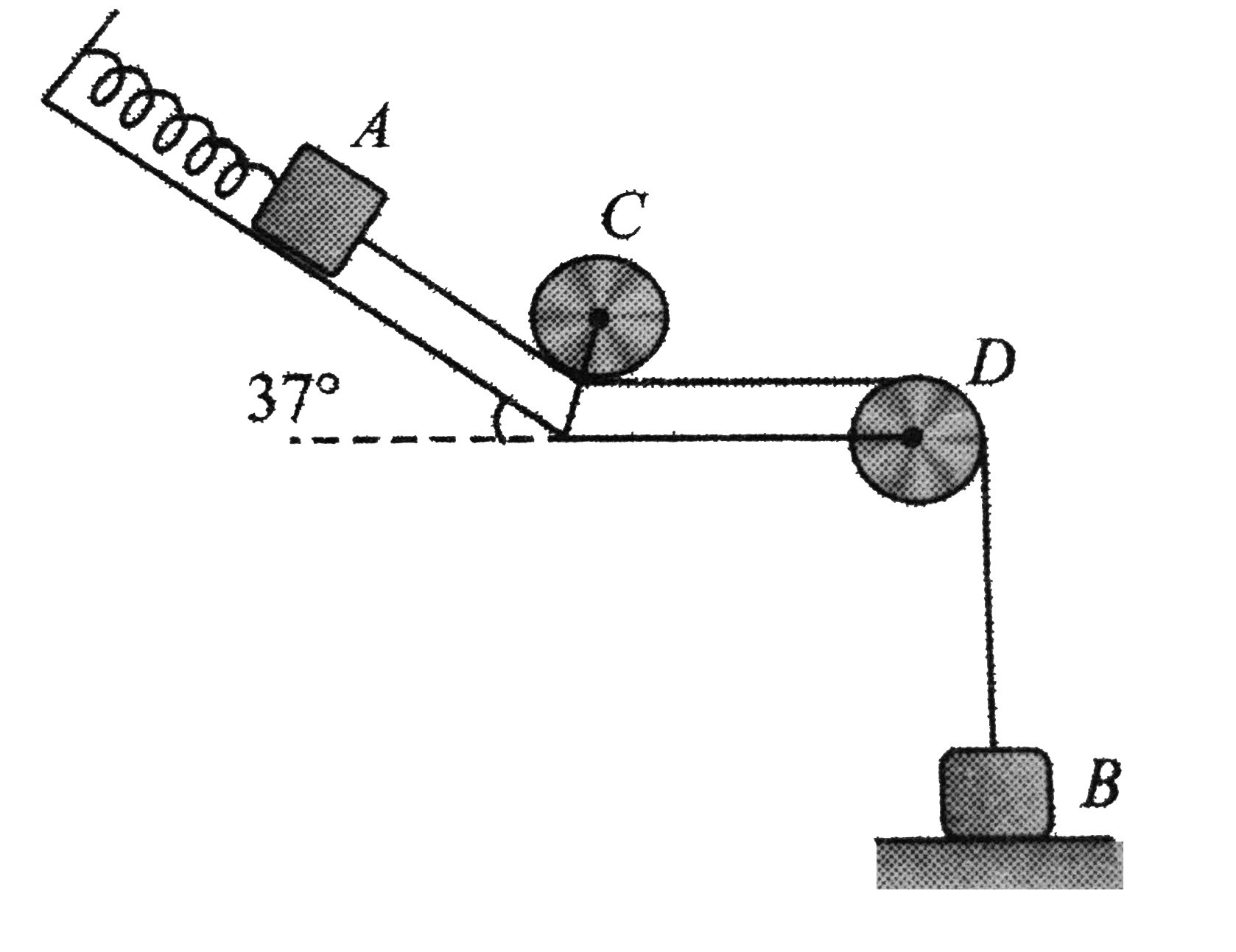
Since the block is released slowly, therefore, it starts to slide down the plane till equilibrium of forces is achieved.
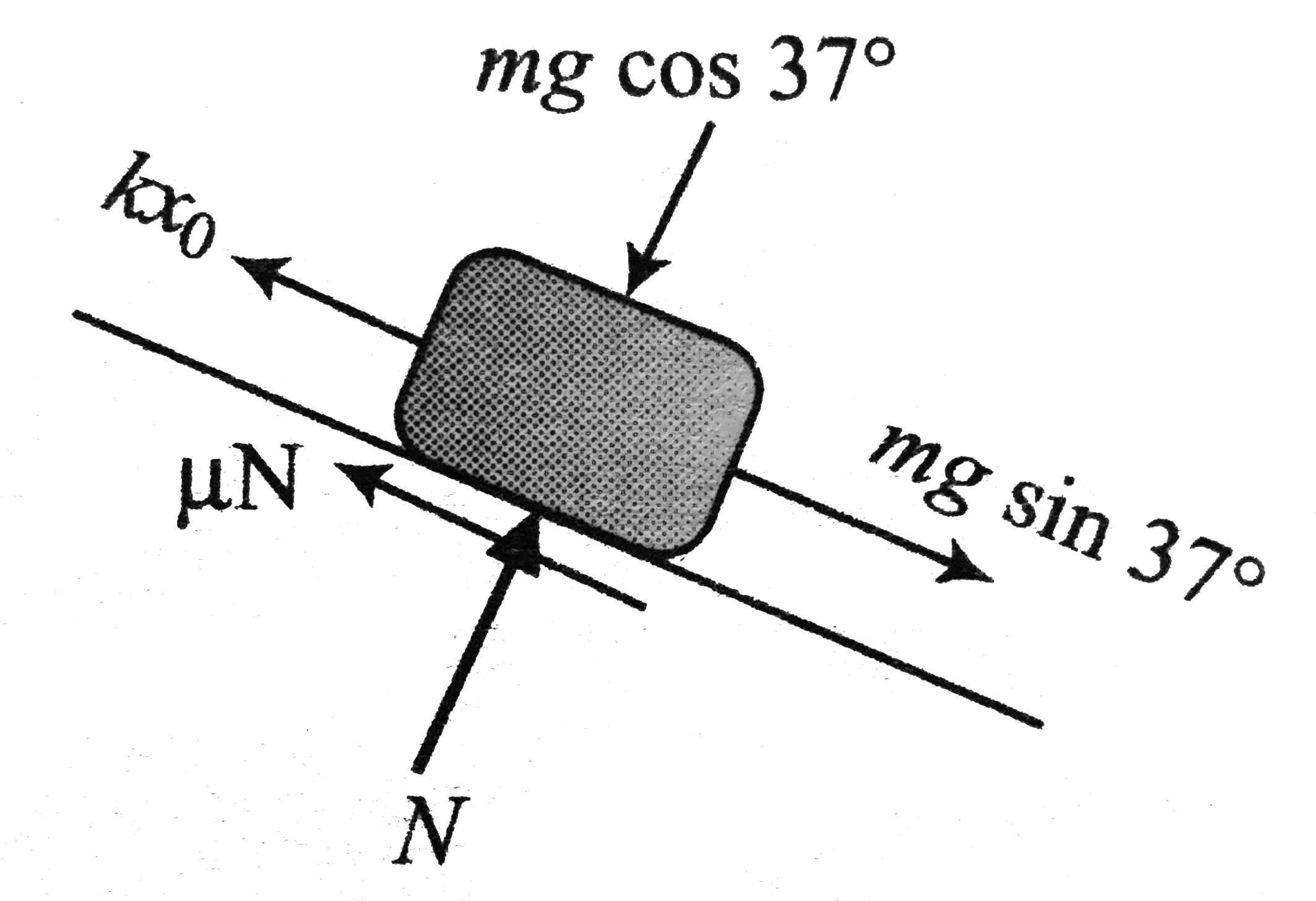
Let at that instant elongation of spring be x0, then tension in it is
T0=Kx0=2000x0
Considering free body diagram of block,
N=mgcos37∘−40N (i)
Kx0+μN=mgsin37∘ (ii)
From Eq. (i) and (ii),
x0=0.01m=1cm
When table collapses, first block B falls freely under gravity through height 80/9. Therefore, its speed just before the string becomes taut is
v0=√2g×(0.809)=43ms−1
Now block A is jerked into motion and a large tension (for a very small time interval) is developed in string due to which both the blocks A and B experience numerically equal impulses.
Let its magnitude be J and let the combined speed of blocks be v.
Then for block A, J=5v (iii)
for block B, 3v0−J=3v (iv)
From equation (iii) and (iv) v=0.5ms−1
At the instant of maximum elongation of spring, blocks are momentarily at rest.
Let distance moved by the blocks be x from the instant when blocks A was jerked into motion to the instant of maximum elongation of the spring.
According to law of consevation of energy,
Loss of potential energy of A+Loss of potential energy of B+
Loss of kinetic energy of blocks=Increase in energy stored in spring+Work done by the block A against friction.
=5.g(xsin37∘)+3gx+{12×(5v2)+12×(3v2)}
={12K(x0+x)2−12Kx20}+μNx
x=0.5mm or 5cm
Maximum elongation of spring= Its initial elongation (x0)+
Further elongation(x)=6cm
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.1
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.2
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (integer)
4 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A small block of mass m=1kg is attached with one end of the spring of force constant K=110Nm−1. Other end of the spring is fixed to a rough plane having coefficient of friction μ=0.2. The spring is kept in its natural length by an inextensible thread ties between its ends as shown in figure. If the thread is burnt, calculate the elongation of the spring when the block attains static equilibrium position.
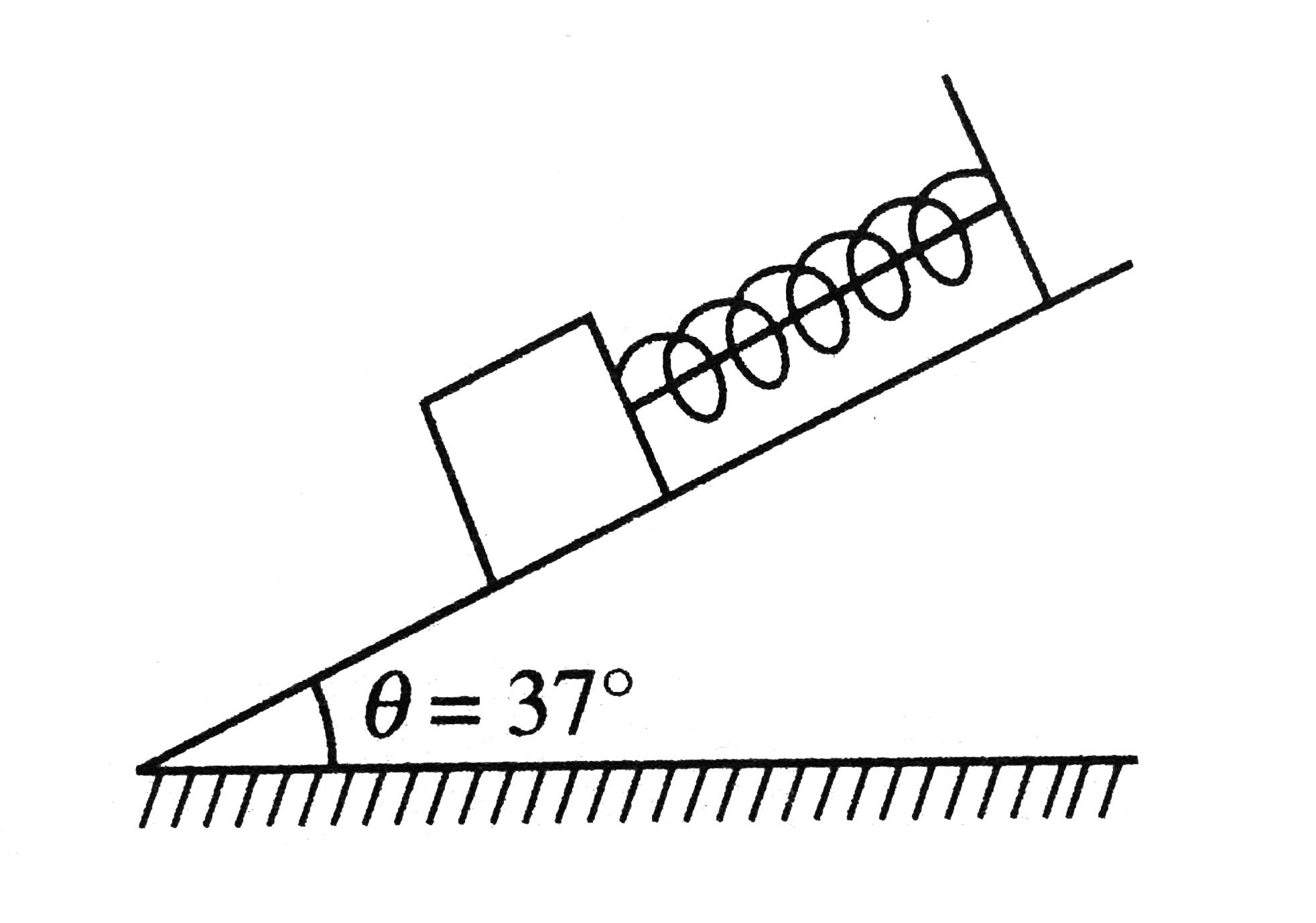
View SolutionA block of mass m attached with a an ideal spring of force constant k is placed on a rough inclined plane having inclination θ with the horizontal and coefficient of friction μ=1/2tanθ, Initially the block is held stationary with the spring in its relaxed state, find the maximum extension in the spring if the block is released.

View Solution
Knowledge Check
Two blocks each having mass m is attached to each other with a spring having force constant k. The system is placed on a rough horizontal surface having coefficient of friction μ. The maximum initial compression, that can be given to the spring so that when released the blocks do not move is
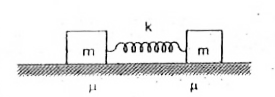 A2μmg/kBμmg/kCzeroDnot possible
A2μmg/kBμmg/kCzeroDnot possibleA block of mass 'm' is attached to a spring in natural length of spring constant 'k'. The other end A of the spring is moved with a constat velocity v away from the block . Find the maximum extension in the spring.
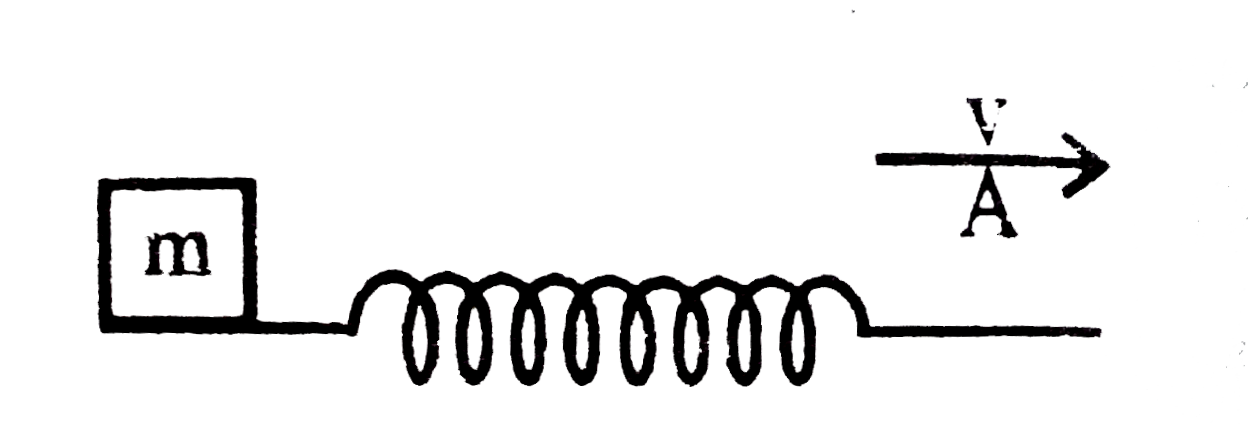 A14√mv2kB√mv2kC12√mv2kD2√mv2k
A14√mv2kB√mv2kC12√mv2kD2√mv2kA block of mass m is attached with a massless spring of force constant k. The block is placed over a rough inclined surface for which the coefficient of friction is μ=34. The minimum value of M required to move the block up the plane is (Neglect mass of string, mass of pulley and friction in pulley)
 A35mB45mC65mD32m
A35mB45mC65mD32m
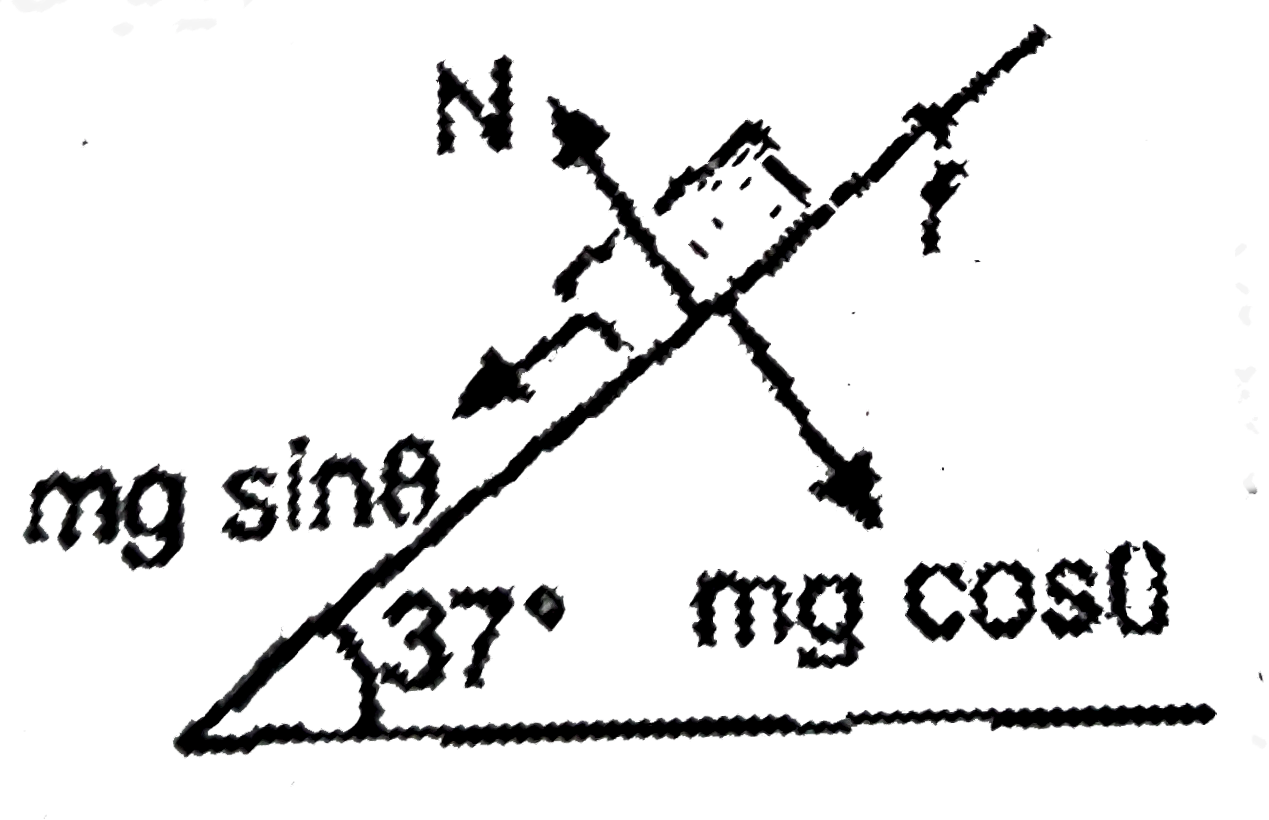
A block of mass 3 kg slides on a rough fixed inclined plane of 37∘ angle having coefficient of friction 0.5. find the resultant force exerted by plane on the block.
View SolutionA block of mass m is attached with a massless spring of force constant K. the block is placed over a rough inclined surface for which the coefficient of friction is μ=34 find the minimum value of M required to move the block up the place. (Neglect mass of string and pulley. Ignore friction in pulley).
 .
.
View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View SolutionA block of mass ''m' is attached with a mass - less spring of force constant k. The block is placed over a rough inclined surface for which the coefficient of friction is μ=3/4. The minimum value of 'M' required so that the block on the inclined plane is at rest (neglect mass of string and pulley).

View SolutionA block of mass m is attached to a spring of force constant k whose other end is fixed to a horizontal surface. Initially the spring is in its natural length and the block is released from rest. The average force acting on the surface by the spring till the instant when the block has zero acceleration for the first time is
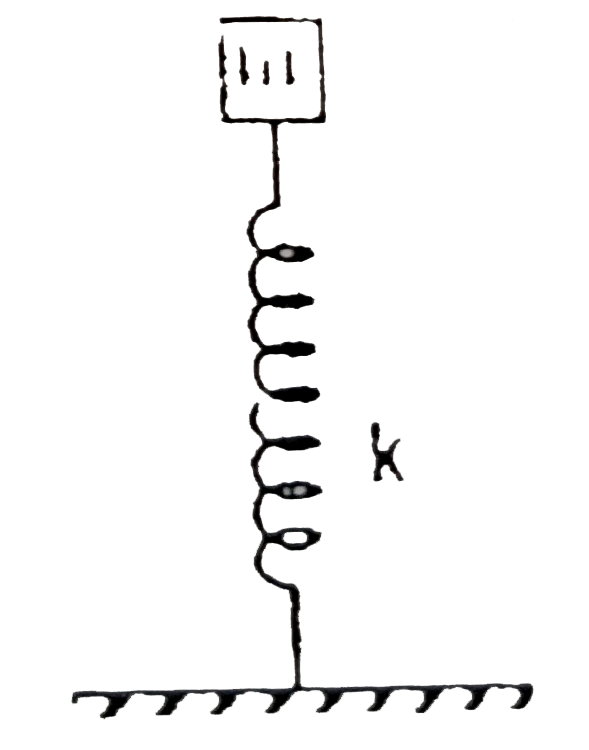
View Solution
