A spherical balll of mass $m$ is the highest point in the space between two fixed , concentic sphere $A$ and $B$ the smaller the two sphere $A$ has a radius $R$ and the space between the two spheres has a width $d$ . The bell has a disneter very dightly less then d . All surface are frictionless . The bell is a given a gentle push (owards the right in the figure ) The upward vertical is denoted by $θ$ (shown ijn the figure)

(a)Express the total normal reaction force exerted by the sphore on the as a finction of angle $θ$
(b) Let N_(A) $and N_{B}$ denote in the magnitubes of the normal reaction force on the bell evered by the sphare $A$ and $B$ repectively Skech the variation of $N_{A} and$ N_(B) $a s f u n c t i o n s o f$ cos theta $\in t h e r a n \geq$ 0 le theta le pi $b y d r a w \in g t w o s e p a r a t e g r a p h \in y o u r a n s w e r b \infty k t a k \in g$ cos theta an the horizental axas.

Video Solution

Text Solution

Verified by Experts

The ball is moving in a circulaar motion. The necessary centripetal force is provided by $(m g cos θ - N)$ . Therefore,
$m g cos θ - N_{A} = \frac{m v^{2}}{{[R + (d / 2)]}^{2}}$ (i)
According to energy conservation,
$\frac{1}{2} m v^{2} = m g (R + \frac{d}{2}) (1 - cos θ)$ (ii)
From Eqs (i) and (ii), we get
$N_{A} = m g (3 cos θ - 2)$ (iii)
The above equation shows that as $θ$ increases, $N_{A}$ decreases. At a particular value of $θ$ , $N_{A}$ will become zero and the ball will lose contact with sphere A. This condition can be found by putting
$N_{A} = 0$ in Eq. (iii).
$0 = m g (3 cos θ - 2)$
$∴ θ = {cos}^{- 1} (\frac{2}{3})$
The graph between $N_{A}$ and $cos θ$ is shown in figure.

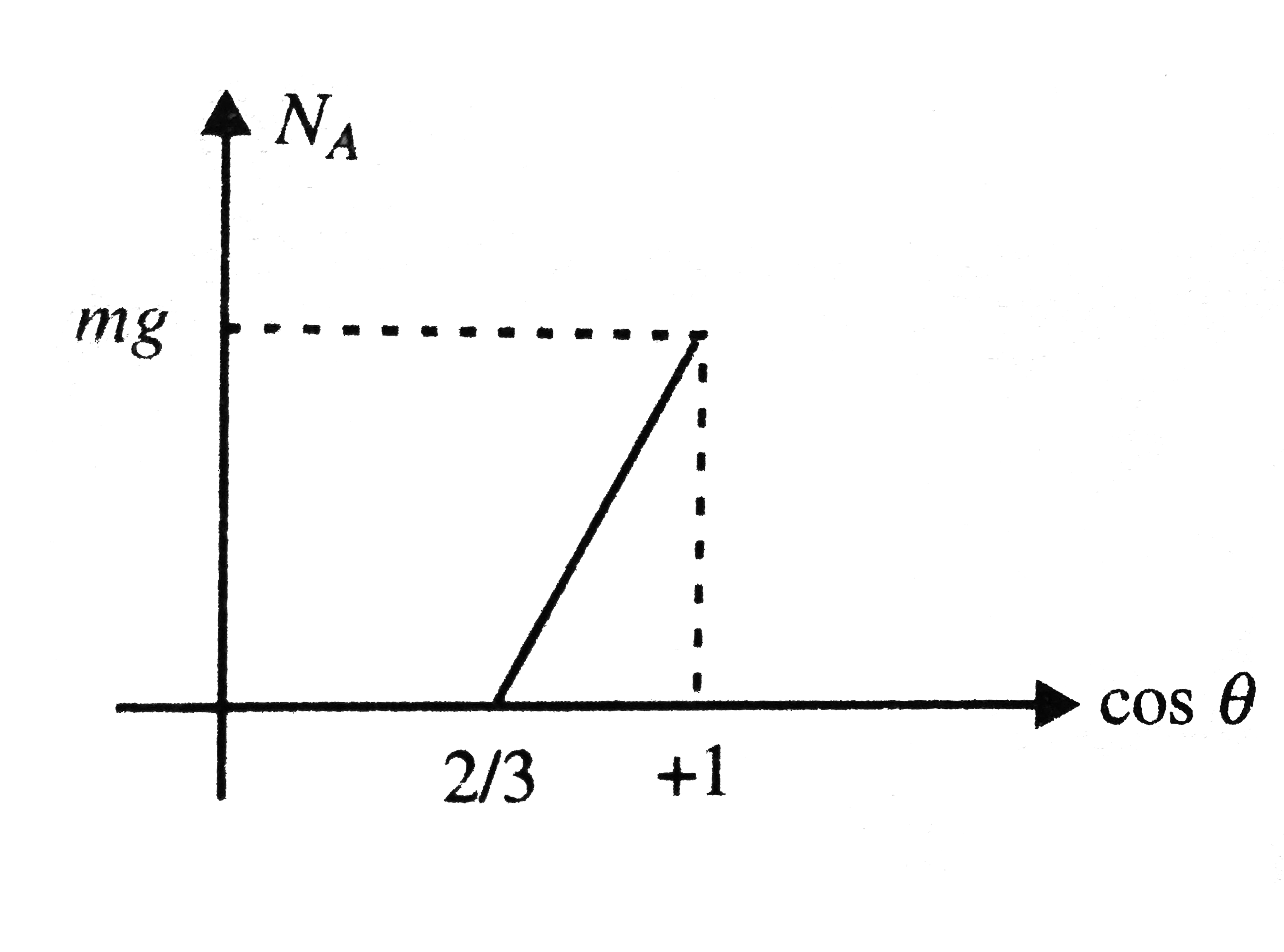
From Eq. (iii), when $θ = 0$ , $N_{A} = m g$ .
When $θ = {cos}^{- 1} (\frac{2}{3})$ , $N_{A} = 0$ .
The graph is a straight line as shown in figure.
When $θ > {cos}^{- 1} (\frac{2}{3})$
$N_{B} + m g cos θ = \frac{m v^{2}}{(R + \frac{d}{2})}$ (iv)
Using energy conservation, we get
$\frac{1}{2} m v^{2} = m g [(R + \frac{d}{2}) - (R + \frac{d}{2}) cos θ]$
$\frac{m v^{2}}{(R + \frac{d}{2})} = 2 m g [1 - cos θ]$
From Eqs. (iv) and (v), we get
$N_{B} + m g cos θ = 2 m g - 2 m g cos θ$
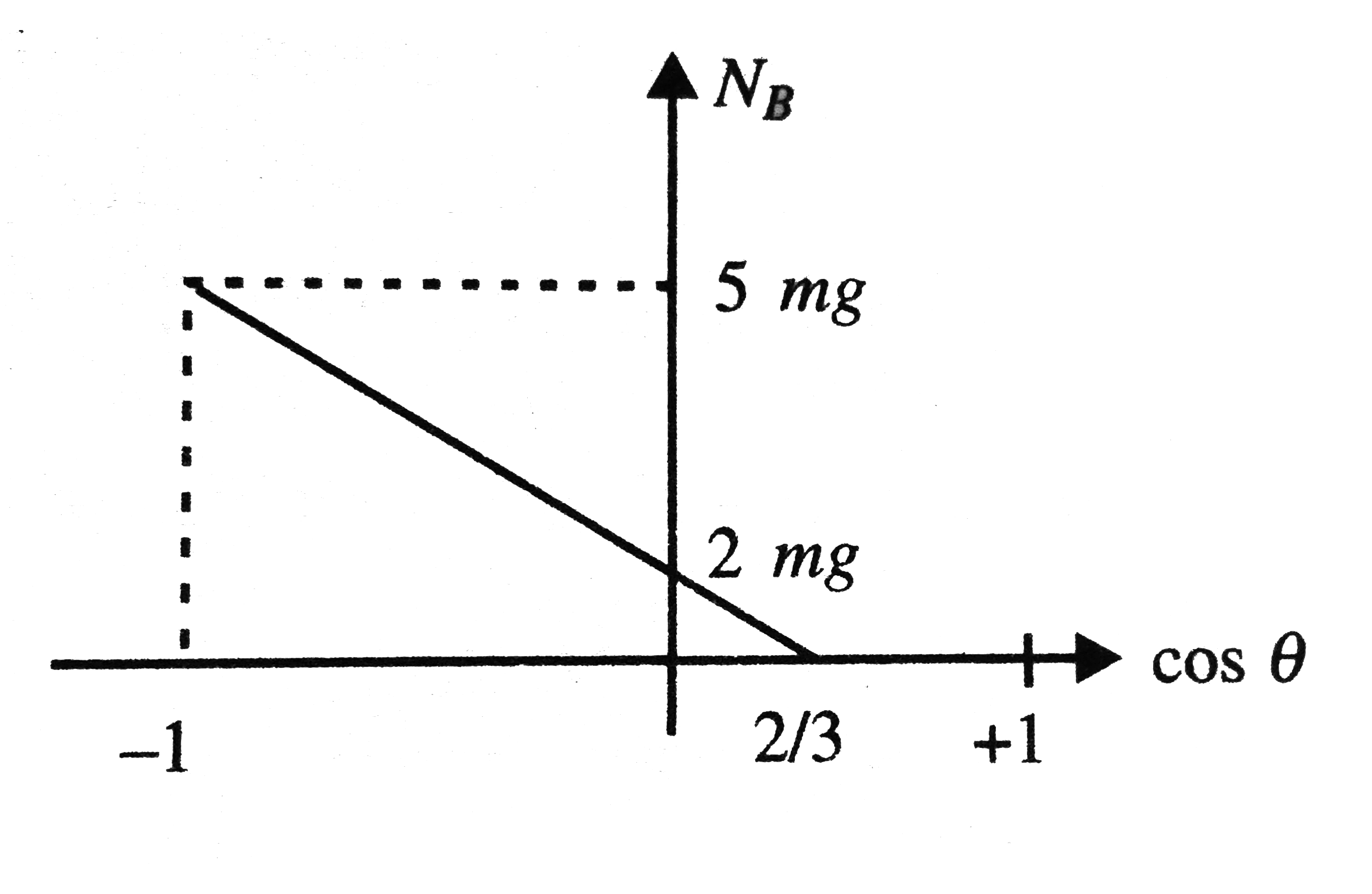
$\Rightarrow N_{B} = m g (2 - 3 cos θ)$
When $cos θ = \frac{2}{3}$ , $N_{B} = 0$
When $cos θ = - 1$ , $N_{B} = 5 m g$
Therefore, the graph is as shown in figure.

Updated on:21/07/2023

Class 11 PHYSICS WORK, ENERGY AND POWER

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
A spherical balll of mass $m$ is the highest point in the space between two fixed , concentic sphere $A$ and $B$ the smaller the two sphere $A$ has a radius $R$ and the space between the two spheres has a width $d$ . The bell has a disneter very dightly less then d . All surface are frictionless . The bell is a given a gentle push (owards the right in the figure ) The upward vertical is denoted by $θ$ (shown ijn the figure)

(a)Express the total normal reaction force exerted by the sphore on the as a finction of angle $θ$
(b) Let N_(A) $and N_{B}$ denote in the magnitubes of the normal reaction force on the bell evered by the sphare $A$ and $B$ repectively Skech the variation of $N_{A} and$ N_(B) $a s f u n c t i o n s o f$ cos theta $\in t h e r a n \geq$ 0 le theta le pi $b y d r a w \in g t w o s e p a r a t e g r a p h \in y o u r a n s w e r b \infty k t a k \in g$ cos theta an the horizental axas.
A $m g (3 cos θ - 2)$
B $m g (2 cos θ - 3)$
C $3 m g (2 cos θ - 1)$
D $2 m g (3 cos θ - 1)$
Question 2 - Select One
A small spherical ball of mass m is projected from lowest point (point P) in the space between two fixed, concentric spheres A and B (see figure). The smaller sphere A has a radius R and the space between the two spheres has a width d. The ball has a diameter very slightly less than d. All surfaces are frictionless. Speed of ball at lowest point is v. NA and NB represent magnitudes of the normal reaction force on the ball exerted by the spheres A and B respectively. Match the value of v given in column–I with corresponding results in column–II.

A $\begin{matrix} Column-I & Column-II (A) v = \sqrt{g R} & (p) maximum value of N_{A} = 0 \end{matrix}$
B $\begin{matrix} Column-I & Column-II (B) v = \sqrt{2 g R} & (q) minimum value of N_{B} = 0 \end{matrix}$
C $\begin{matrix} Column-I & Column-II (C) v = \sqrt{3 g R} & (r) maximum value of N_{B} = 6 m g \end{matrix}$
D $\begin{matrix} Column-I & Column-II (D) v = \sqrt{5 g R} & (s) maximum value of N_{B} = 4 m g (t) maximum value of N_{B} = 2 m g \end{matrix}$
Question 3 - Select One
The electric field between the two spheres of a charged spheres condenser
Ais zero
Bis constant
Cincrease with distance from centre
Ddecrease with distance from centre

CENGAGE PHYSICS-WORK, POWER & ENERGY-Solved Examples

Home
Ask Doubt
Profile

Topper's Solved these Questions

Similar Questions

Knowledge Check

The electric field between the two spheres of a charged spheres condenser

CENGAGE PHYSICS-WORK, POWER & ENERGY-Solved Examples