A single conservative force acting on a particle varies as →F=(−Ax+Bx2)ˆiN, where A and B are constants and x is in meters. (a) Calculate the potential energy function U(x) associated with this force, taking U=0 at x=0. (b) Find the change in potential energy and the change in kinetic energy of the system as the particles moves from x=2.00m to x=3.00m.
a. U=−x∫0(−Ax+Bx2)dx=Ax22−Bx33
b. ΔU=−3.00m∫2.00mFdx
=A[(3.00)2−(2.00)2]2−A[(3.00)3−(2.00)3]3
=5.002A−19.03B
ΔK=(−5.002A+19.03B)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.326videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.416videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.125videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
Potential energy of a particle along x-axis varies as U = - 30 + (X−2)2, where U is in joule and x is in meter. Hence the particle is in
View SolutionForce acting on a particle varies with x as shown in figure. Calculate the work done by the force as the particle moves from x = 0 to x = 6.0 m.
View Solution
Knowledge Check
- Question 1 - Select One or More
The potential energy of a particle is given by formula U=100−5x+100x2,whereU and are .
AAt 0.05m form the origin is 50 ms^(2).BAt 0.05 m from the mean position is 100 ms^(2).CAt 0.05 m feom the origin is 150 ms^(2).DAt 0.05m from the mean position is 200ms−1 - Question 2 - Select One
A force acting on particle is given by →F=(3x2ˆi+4yˆj)N. The change in kinetic energy of particle as it moves from (0,2m) to (1m,3m) is
A6JB10JC11JD13J - Question 3 - Select One
A particle free to move along x-axis is acted upon by a force F=−ax+bx2whrteaandbarepositiveconstants.For ximplies0, the correct variation of potential energy function U(x) is best represented by.
A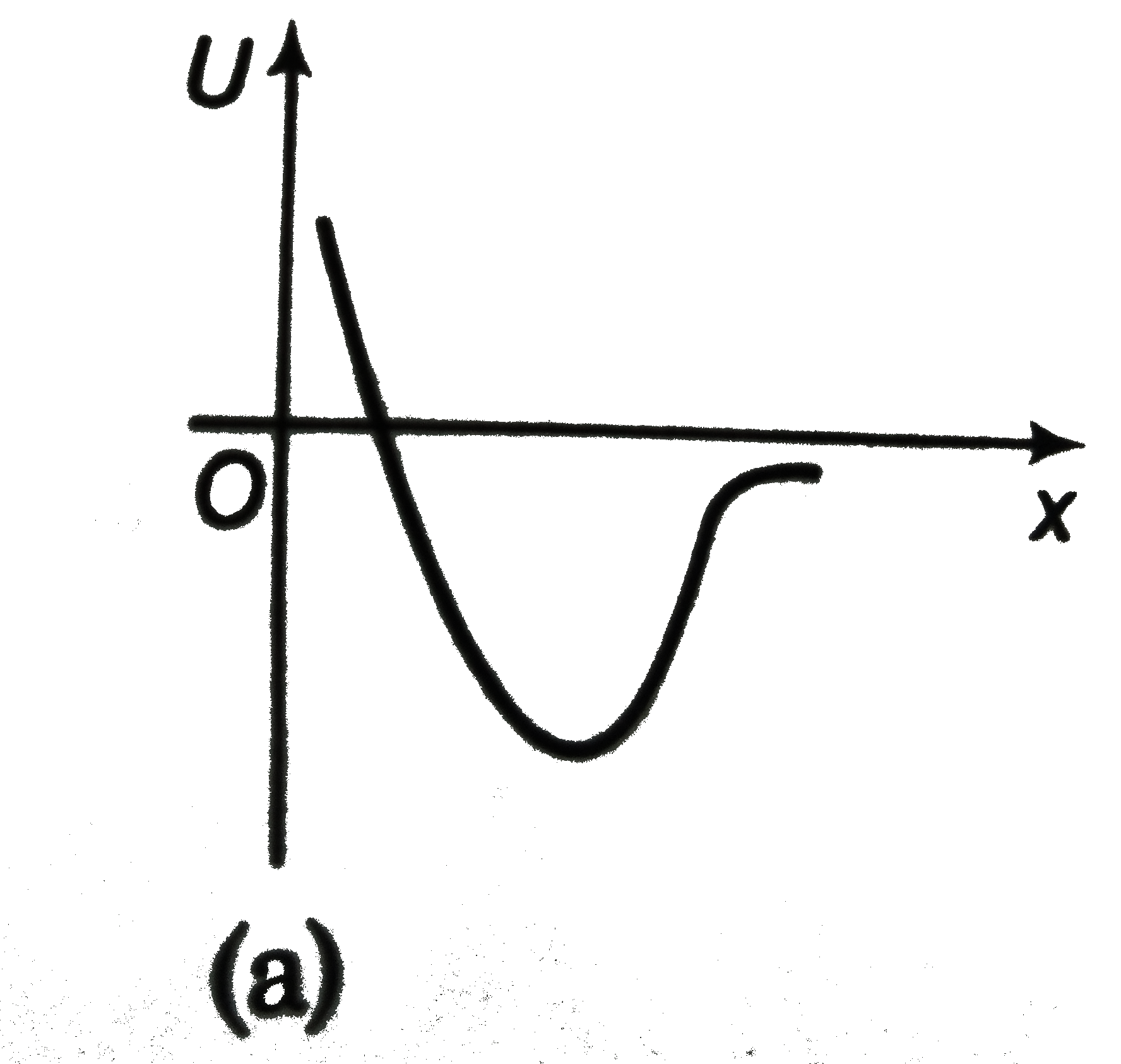 B
B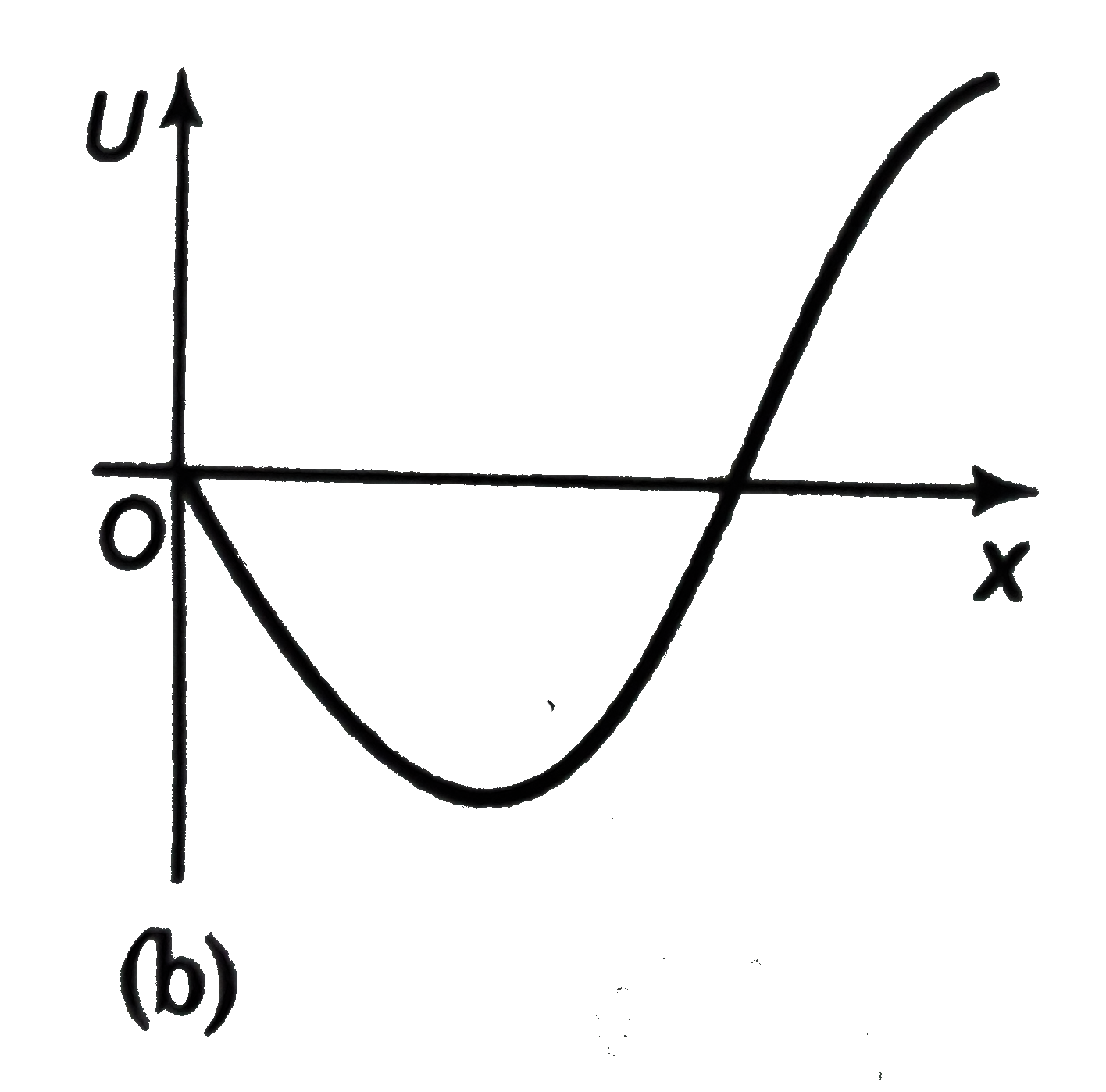 C
C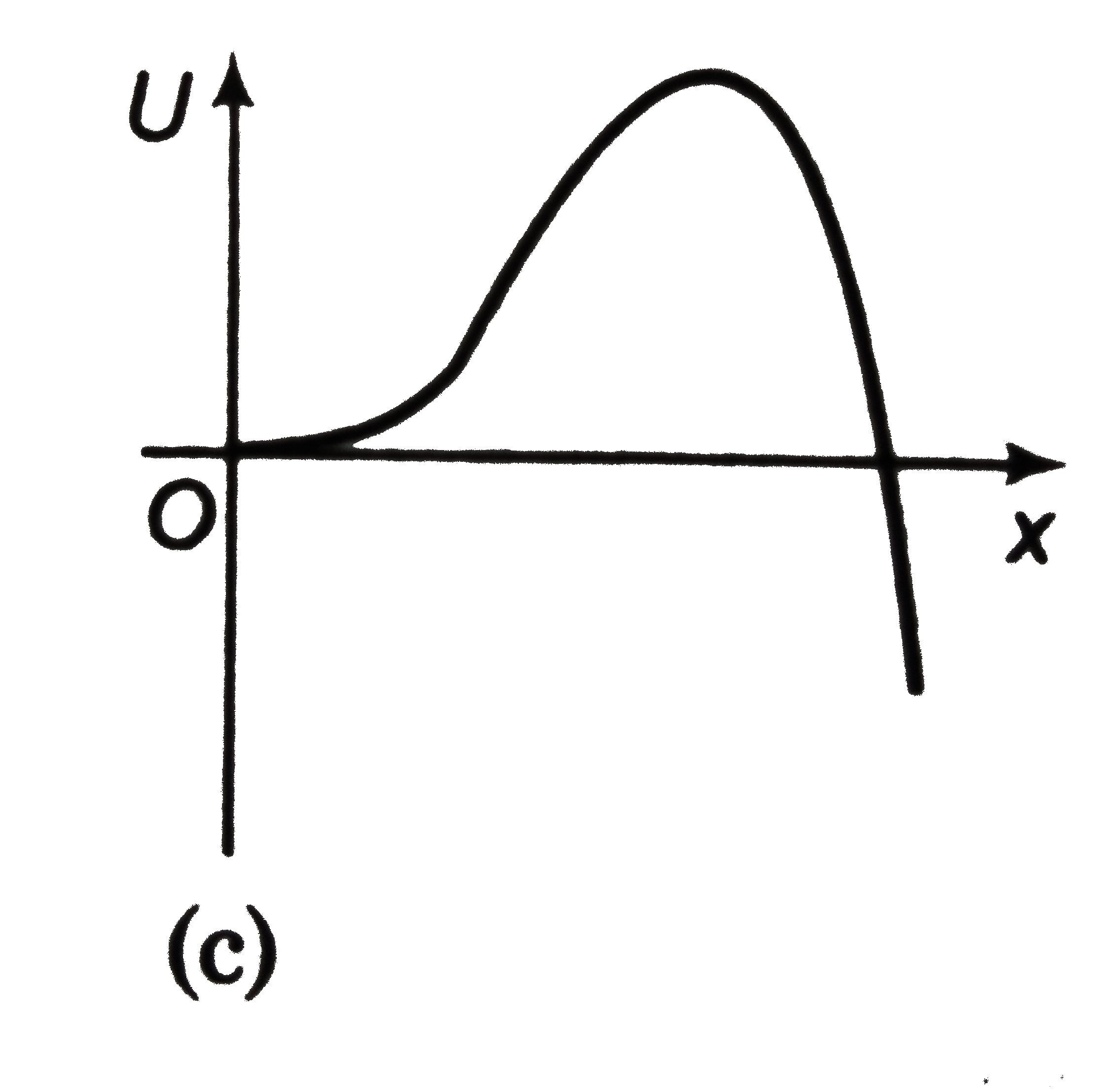 D
D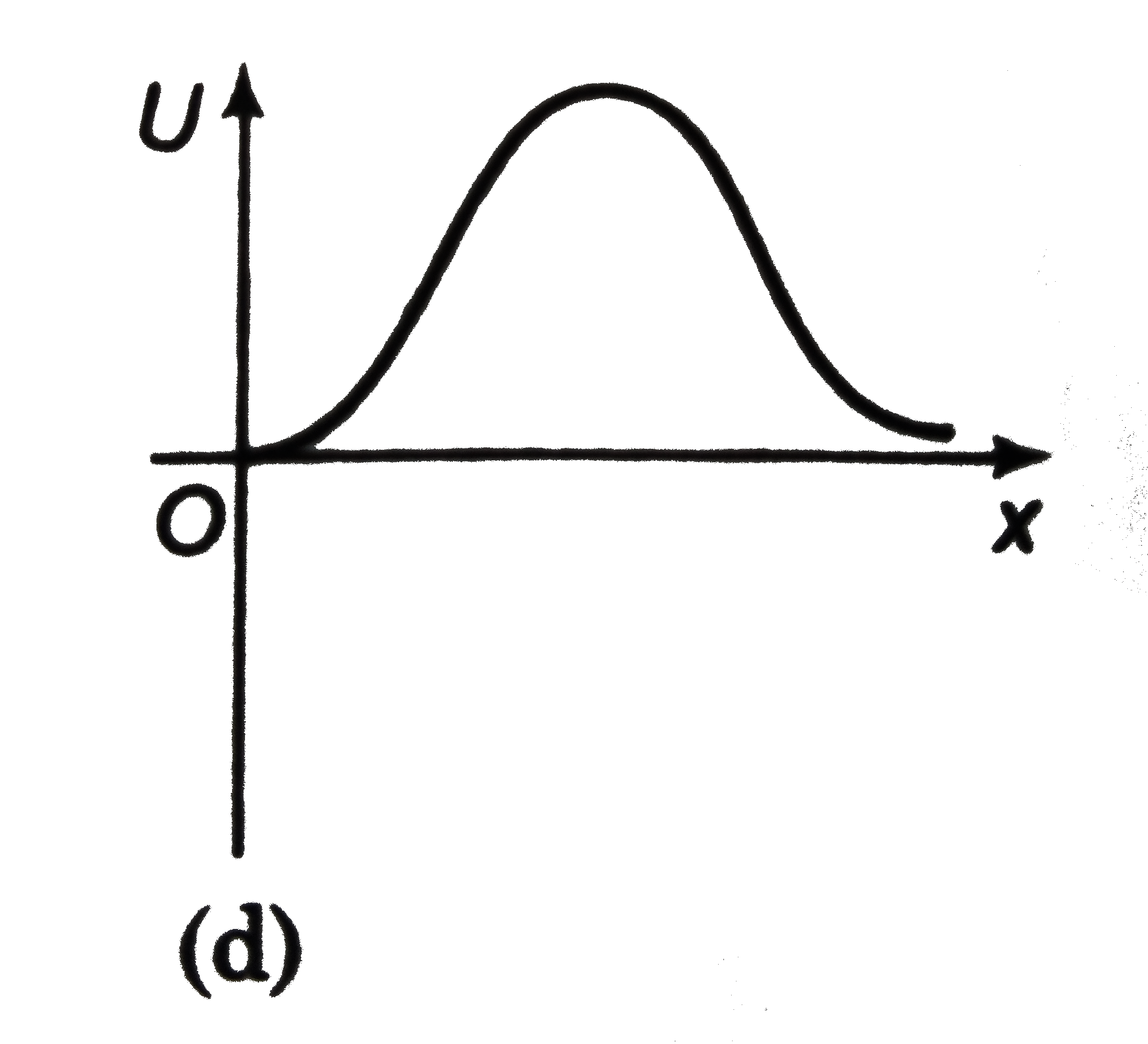
The potential energy of configuration changes in x and y directions as U=kxy, where k is a positive constant. Find the force acting on the particle of the system as the function of x and y.
View SolutionThe potential energy of a particle of mass m is given by U(x)=U0(1−coscx) where U0 and c are constants. Find the time period of small oscillations of the particle.
View SolutionThe potential energy for a conservative force system is given by U=ax2−bx. Where a and b are constants find out (a) The expression of force (b) Potential energy at equilibrium.
View SolutionThe potential energy of a particle in a force field is:
U=Ar2−Br,. Where A and B are positive
constants and r is the distance of particle from the centre of the field. For stable equilibrium the distance of the particle isView SolutionIf x,F and U denote the dispalcement, force acting on and potential energy of a particle then
View Solution

