Find the maximum energy stored in the spring shown in figure, for which the block remains stationary on the rough horizontal surface.

Let the spring be compressed by x. The potential energy stored in the spring =U=(1/2)Kx2 for maximum potential energy in the spring, this deformation has to be maximum to ensure maximum spring force Kx. Since the block is in equilibrium along horizontal, ∑fx=0⇒f−Kx=0 where f=f⇒forKx to be maximum the frictional force must be maximum. The maximum frictional force required to keep the block in equilibrium=limiting frictional force.
N−mg=0⇒N=mg
Therefore, fmax=μmg
kxmax=μmg⇒xmax=μmgk
The maximum potential energy stored in the spring
12kx2max=12k(μmgk)2=μ2m2g22k

Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.3
26 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.4
16 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.1
25 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
Find the elastic potential energy stored in each spring shown in figure, when the block is in equilibrium. Also find the time period of vertical oscillation of the block.

View SolutionA block of mass m1 connected with another of mass m2 by a light spring of natural length l0 and stiiffness k is kept stationary on a rough horizontal surface . The coefficient of friction between m1 and surface is μ and the block m2 is smooth .The block m2 is moved with certain the block m1 in horizontal plane Find the (a) maximum to m1 and (b) acceleration of m2 in part(a)
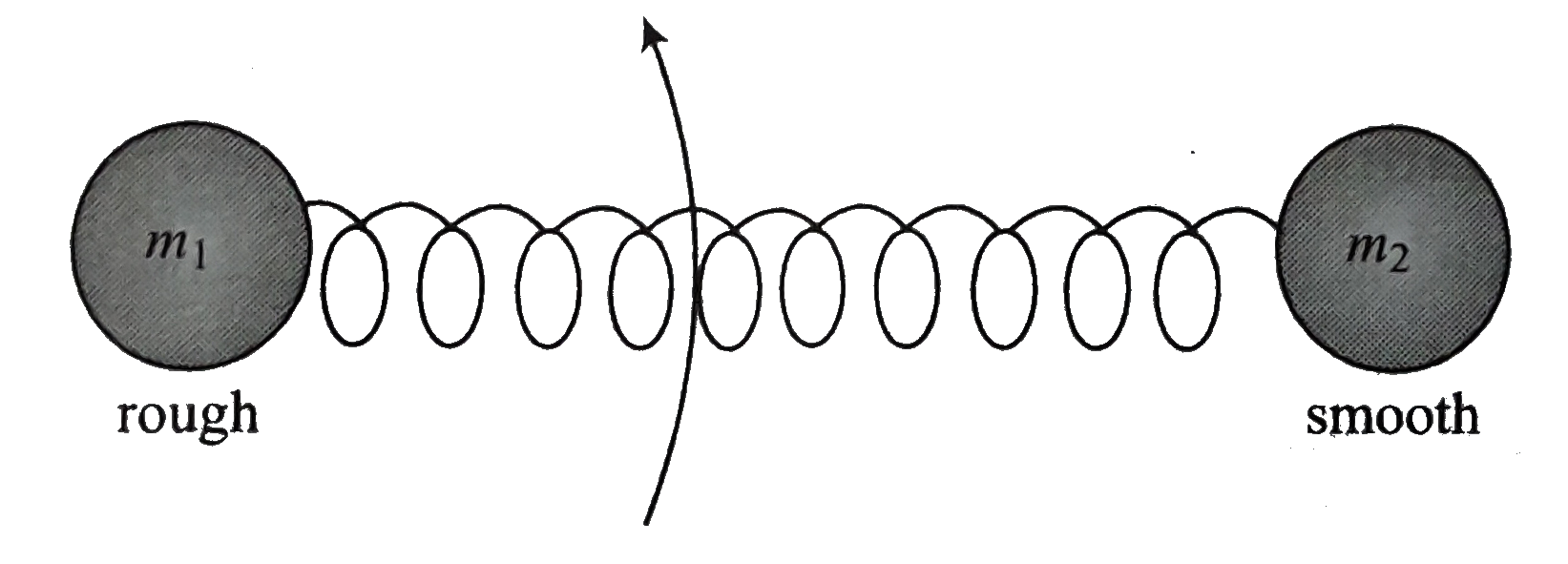
View Solution
Knowledge Check
A spring, placed horizontally on a rough surface is compressed by a block of mass m, placed on the same surface so as to store maximum energy in the spring. If the coefficient of friction between the block and the surface is μ, the potential energy stored in the spring is
Aμ2m2g22kB2μm2g2kCμ2m2g2kD3μ2mg2kA block of mass √3/10kg is placed on a rough horizontal surface as shown in the figure. A force of 1N is applied at one end of the block and the block remains stationary. The normal force exerted by the sruface on the block acts(g=10m/s2)
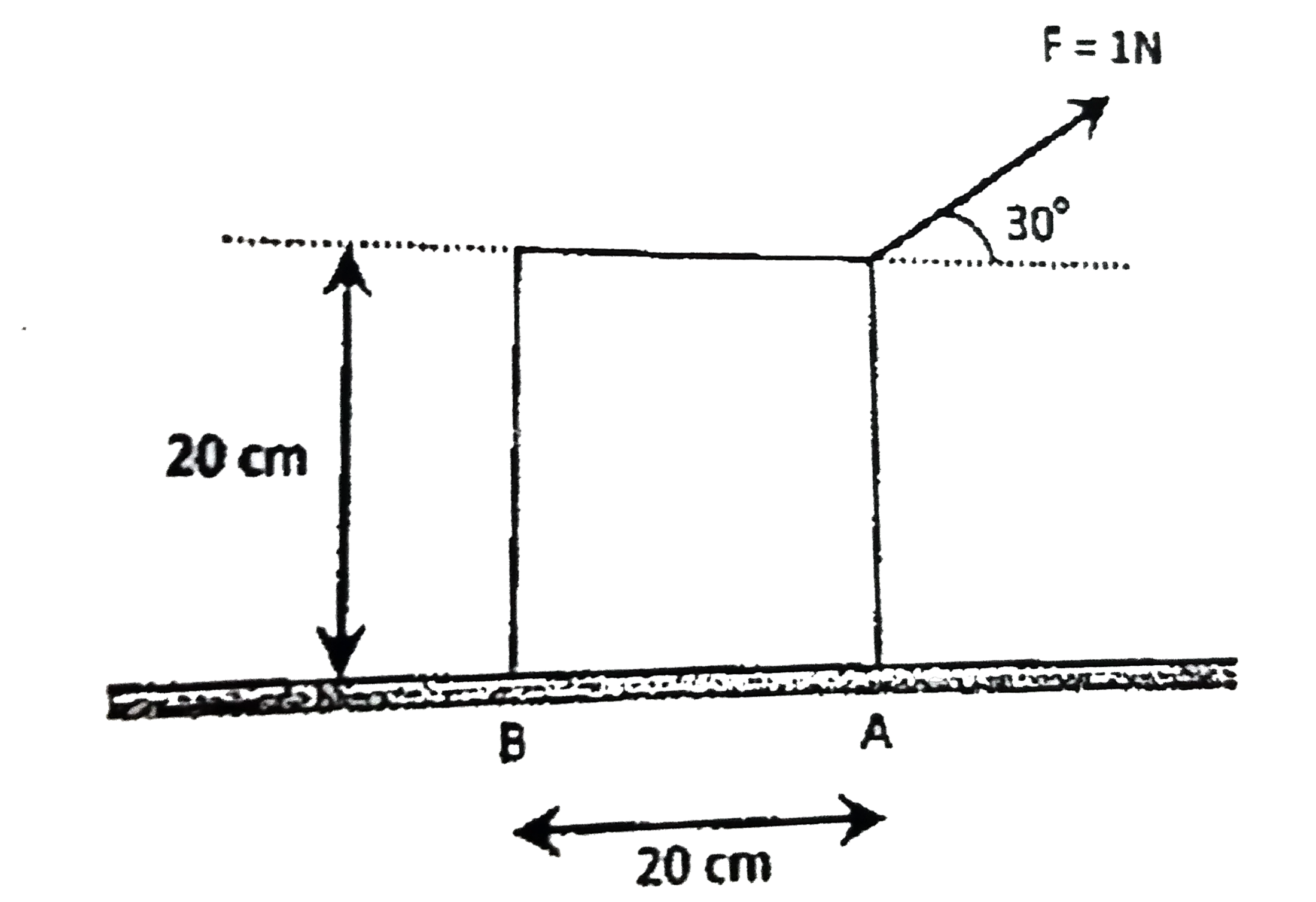 Athrough the center of mass of the blockBthrough point A.Cthrough point B.Dthrough the point at a distance 5cm. From A
Athrough the center of mass of the blockBthrough point A.Cthrough point B.Dthrough the point at a distance 5cm. From AA block of mass 1kgis placed on a rough horizontal surface. A spring is attached to the block whose other end is joined to a rigid wall, as shown in the figure. A horizontal force is applied on the block so that it remains at rest while the spring is elongated by x(x≥μmgk). Let Fmax and Fmin be the maximum and minimum values of force F for which the block remains in equilibrium. For a particular x,Fmax−Fmin=2N. Also shown is the variation of Fmax+Fmin versus x, the elongation of the spring.
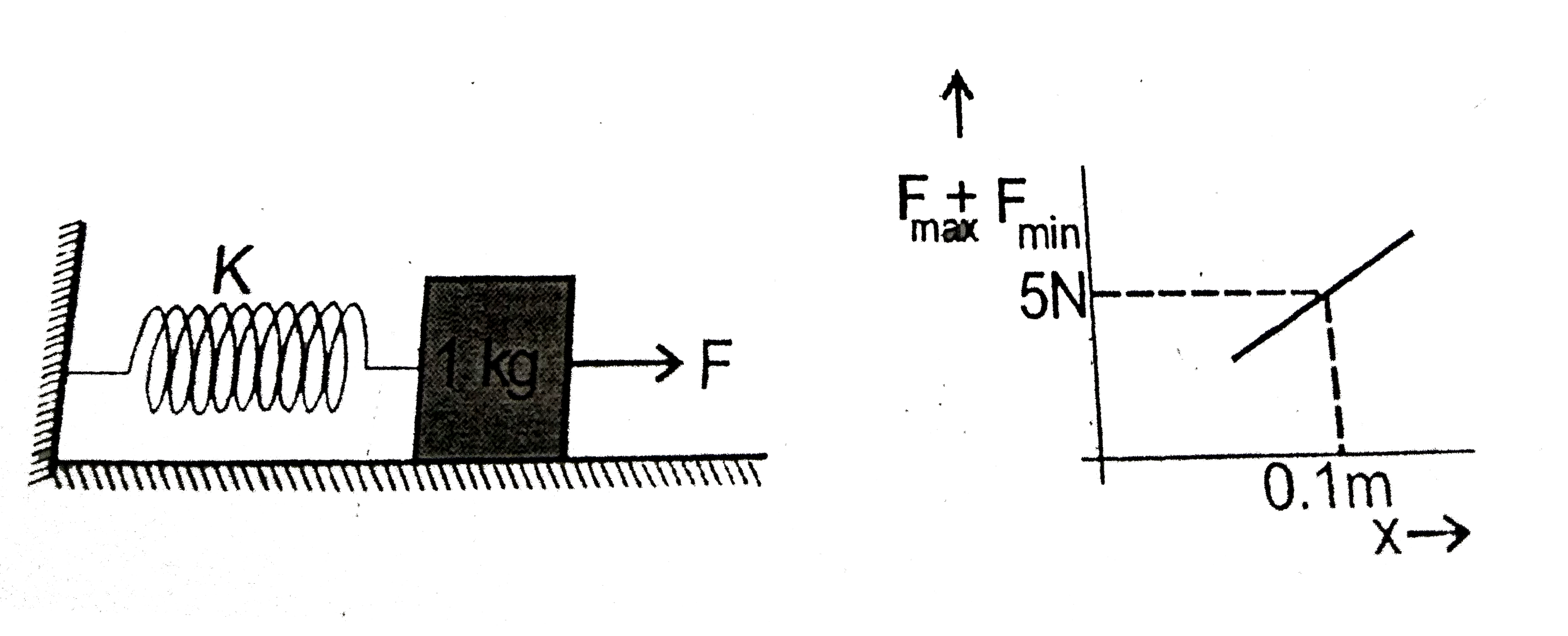
The coefficient of friction between the block and the horizontal surface is :A0.1B0.2C0.3D0.4
A block of mass m held touching the upper end of a light spring of force constant K as shown in figure. Find the maximum potential energy stored in the spring if the block is released suddenly on the spring.

View SolutionAll surfaces are smooth in the adjoining figure. Find F such that block remains stationary with respect to wedge.
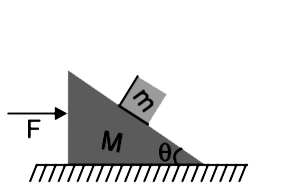
View SolutionAll surface are smooth in following figure. Find F, such that block remain stationary with respect to wedge.

View SolutionFind the magnitude of the horizontal force F required to keep the block of mass m stationary on the smooth inclined plane as shown in the figure.

View SolutionA uniform cubical block is sliding on rough surface as shown. Find possible line of action of normal reaction acting on the block due to rough horizontal surface.
View Solution
