A particle is projected in gravity with a speed v0. Using W-E theorem, find the speed of the particle as the function of vertical distance y.
Let the particle move up through a height y between points 1 and 2. The work done by gravity in shifting the particle from point 1 to 2 is
Wgr=−mgy

The change in kinetic energy is
ΔK=12m(v2−v20)
Substituting W=Wgr=−mgy and ΔK=12m(v2−v20) in W−E theorem, W=ΔK, we have
m2(v2−v20)=−mgy
This gives v=√v20−2gy
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.326videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.416videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.125videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
A particle moves in the x-y plane according to the law x=t2, y = 2t. Find:
(a) velocity and acceleration of the particle as a function of time,
(b) the speed and rate of change of speed of the particle as a function of time,
(c) the distance travelled by the particle as a function of time.
(d) the radius of curvature of the particle as a function of time.View SolutionA heavy particle hanging from a string of length l is projected horizontally with speed √gl. Find the speed of the particle at the point where the tension in the string equals weight of the particle.
View Solution
Knowledge Check
- Question 1 - Select One
A uniform electric field →E in the y-direction and uniform magnetic field →B in the x-direction exists in free space. A particle of mass m and carrying charge g is projected from the origin with speed v0 along the y axis. The speed of the particle as a function of its y coordinate will be
A√v20+2qEymB√v20+qEymC√v20+4qEymDv0 - Question 2 - Select One
A heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizontally with speed (gl) . Then the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string equal the weight of the particle-
A√31g,cos−1(3/2)B√1g3,cos−1(2/3)C√3g3,cos−1(2/3)D√gl3,cos−1(2/3) - Question 3 - Select One
A particle is projected with a speed u at an angle θ with the horizontal. What will be the speed of the particle when direction of motion of particle is at an angle α with the horizontal?
AucosθsecαBusecθcosαCucosθtanαDucosθcotα
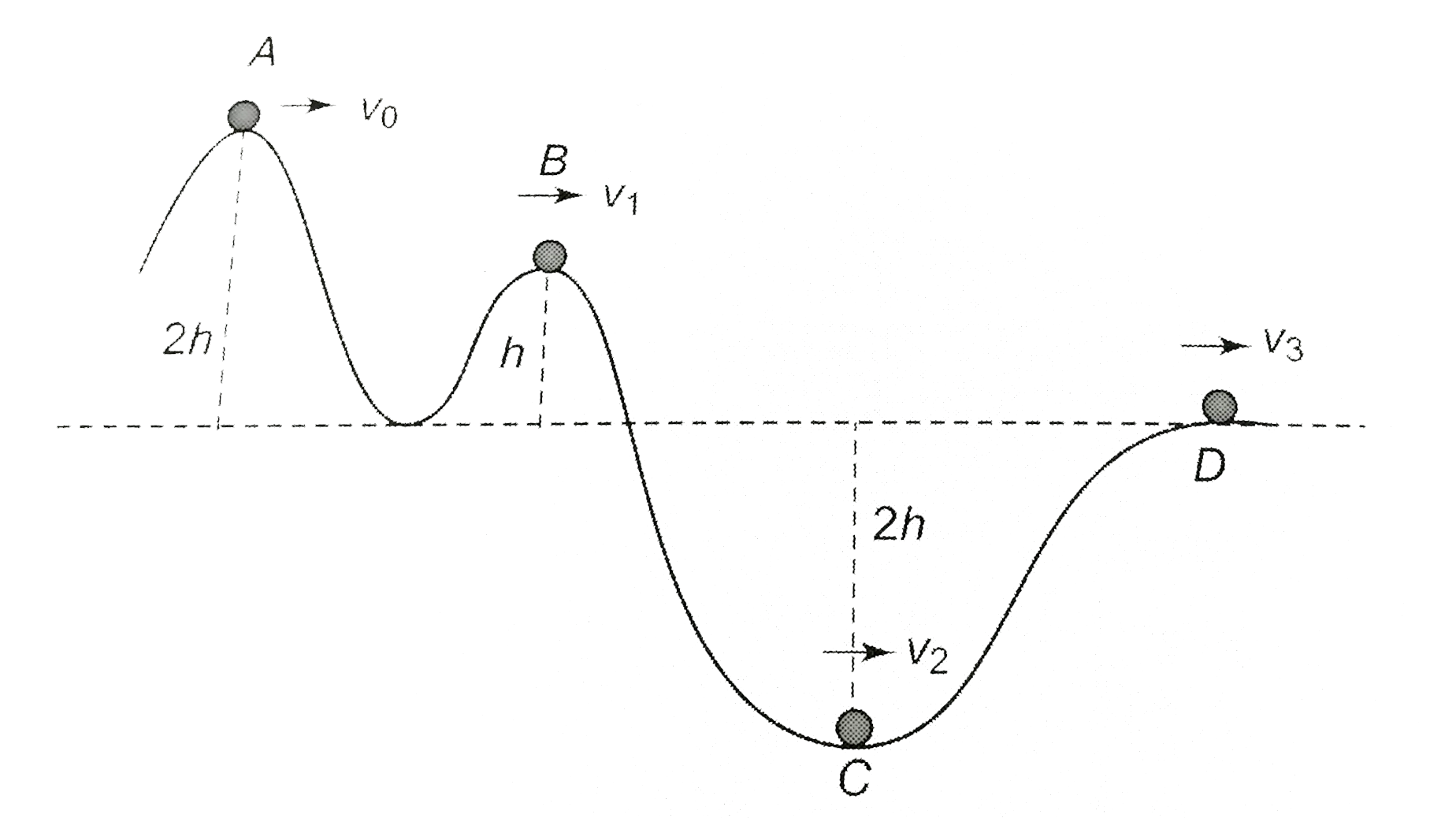
A particle is given velocity v0 at point A as shown in the figure. Find the speed of particle at point B,C and DView SolutionA particle is projected on an inclined plane with a speed u as shown in (Fig. 5.61). Find the range of the particle on the inclined plane.
 .View Solution
.View SolutionA particle is projected vertically upwards in vacuum with a speed u.
View SolutionTwo particles A and B are projected simultaneously from a fixed point of the ground. Particle A is projected on a smooth horizontal surface with speed v, while particle B is projected in air with speed v, while particle B is projected in air with speed 2v√3. If particle B hits the particle A, the angle of projection of B with the vertical is
View SolutionA particle is projected with a speed v0=√gR. The coefficient of friction the particle and the hemi- spherical plane is μ=0.5 Then , the acceleration of the partical is
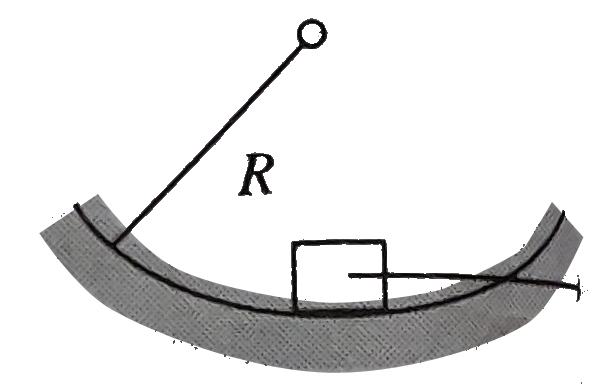 View Solution
View Solution

