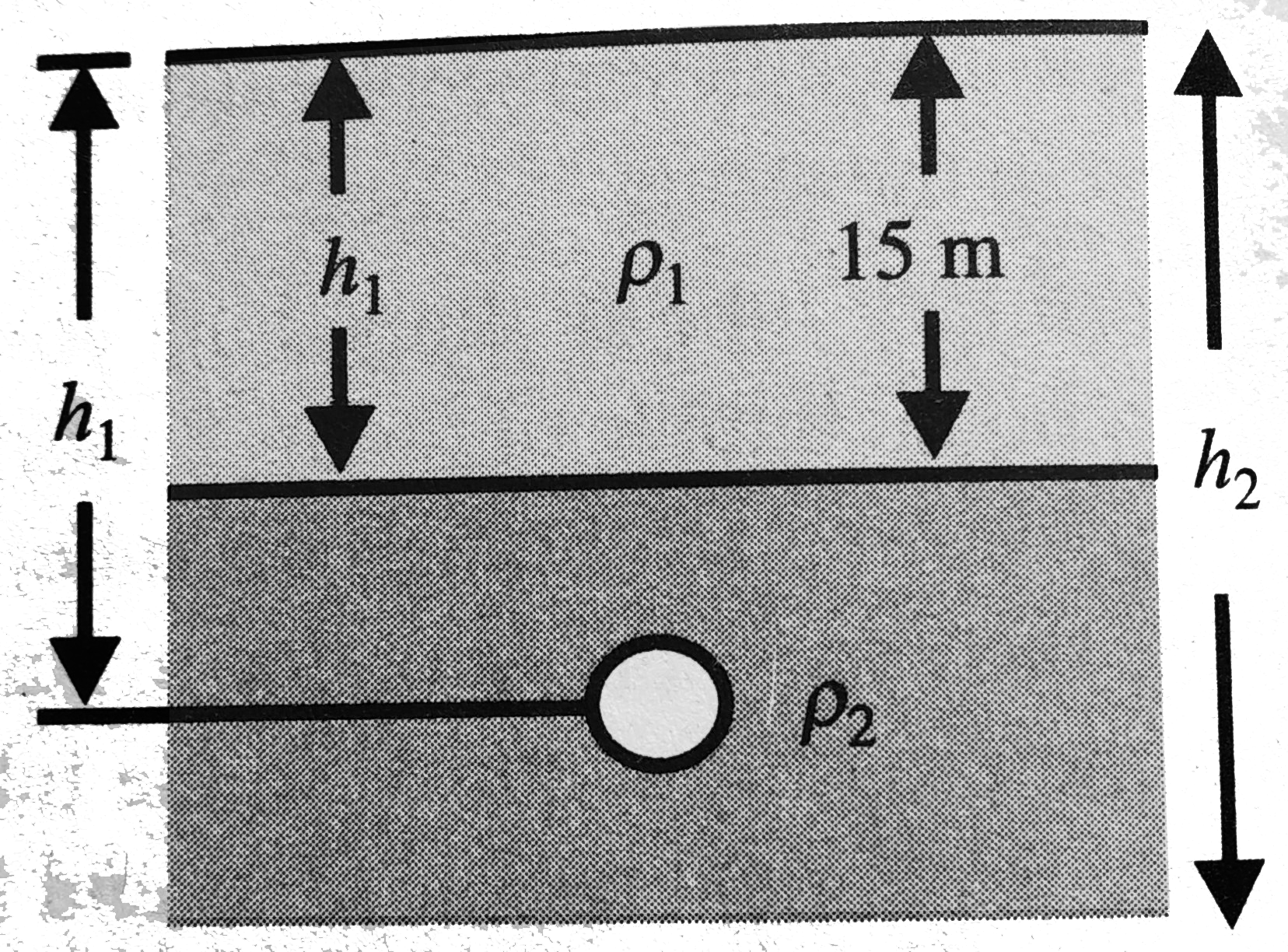
Calculate the pressure inside a small air bubble of radus $r$ situated at a depth $h$ below the free surface of liquids of densities $ρ_{1}$ and $ρ_{2}$ and surface tennsions $T_{1}$ and $T_{2}$ . The thickness of the first and second liquids are $h_{1}$ and $h_{2}$ respectively. Take atmosphere pressure $= P_{0}$ .

A

$P_{0} + ρ_{1} g h_{1} + ρ_{2} g (h - h_{1}) - \frac{2 T_{2}}{r}$

B

$P_{0} + ρ_{1} g h_{1} + ρ_{2} g (h - h_{1}) + \frac{2 T_{2}}{r}$

C

$P_{0} - ρ_{1} g h_{2} + ρ_{2} g (h - h_{1}) + \frac{2 T_{2}}{r}$

D

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$P_{C} = P_{B} + \frac{2 T}{r}$
$P_{B} = P_{A} + ρ_{1} g_{1} = ρ - 2 g (h - h_{1})$

where $P_{A} = P_{0}$
$P_{C} = P_{0} + ρ_{1} g h_{1} + ρ_{2} g (h - h_{1}) + \frac{2 T_{2}}{r}$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The pressure at depth h below the surface of a liquid of density $ρ$ open to the atmosphere is
Agreater than the atmospheric pressure by $ρ g h$
Bless than the atmospheric pressure by $ρ g h$
Cequal to the atmospheric pressure
Dincreases exponentially with depth
Question 2 - Select One
The pressure inside a liquid of density $ρ$ at a depth h is :
A $h ρ g$
B $\frac{h}{ρ g}$
C $\frac{h ρ}{g}$
D $h ρ$

CENGAGE PHYSICS ENGLISH-MISCELLANEOUS VOLUME 2-INTEGER_TYPE

Home
Ask Doubt
Profile