Two particles of masses m1 and m2 are connected by a light and inextensible string which passes over a fixed pulley. Initially, the particle m1 moves with velocity v0 when the string is not taut. Neglecting friction in all contacting surface, find the velocities of the particles m1 and m2 just after the string is taut.

During the impact a large tension develops. The impulse of tension T1 is equal to the change of momentum of m1 which is given as
m1v0−J=m1v

Similarly the impulse of tension T2 is equal to the change in momentum of m2 which is given as
J=m2v......ii
from eqn i and ii we have
m1(v0−v)=m2v
This gives v=m1v0m1+m2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Solved Examples13videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.120videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
Similar Questions
Two blocks of masses m1 and m2 are attached at the ends of an inextensible string which passes over a smooth massless pulley. If m1>m2, find :
(i) the acceleration of each block
(ii) the tension in the string.
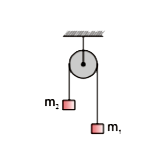 View Solution
View SolutionTwo masses M and m are connected at the two ends of an inextensible string. The string passes over a smooth frictionless pulley. Calculate the acceleration of the masses and the tension in the string. Given M>m.
View Solution
Knowledge Check
- Question 1 - Select One or More
Two masses m1 and m2 are connected by light inextensible string passing over a smooth pulley P. If the pulley moves vertically upwards with an acceleration equal to g then
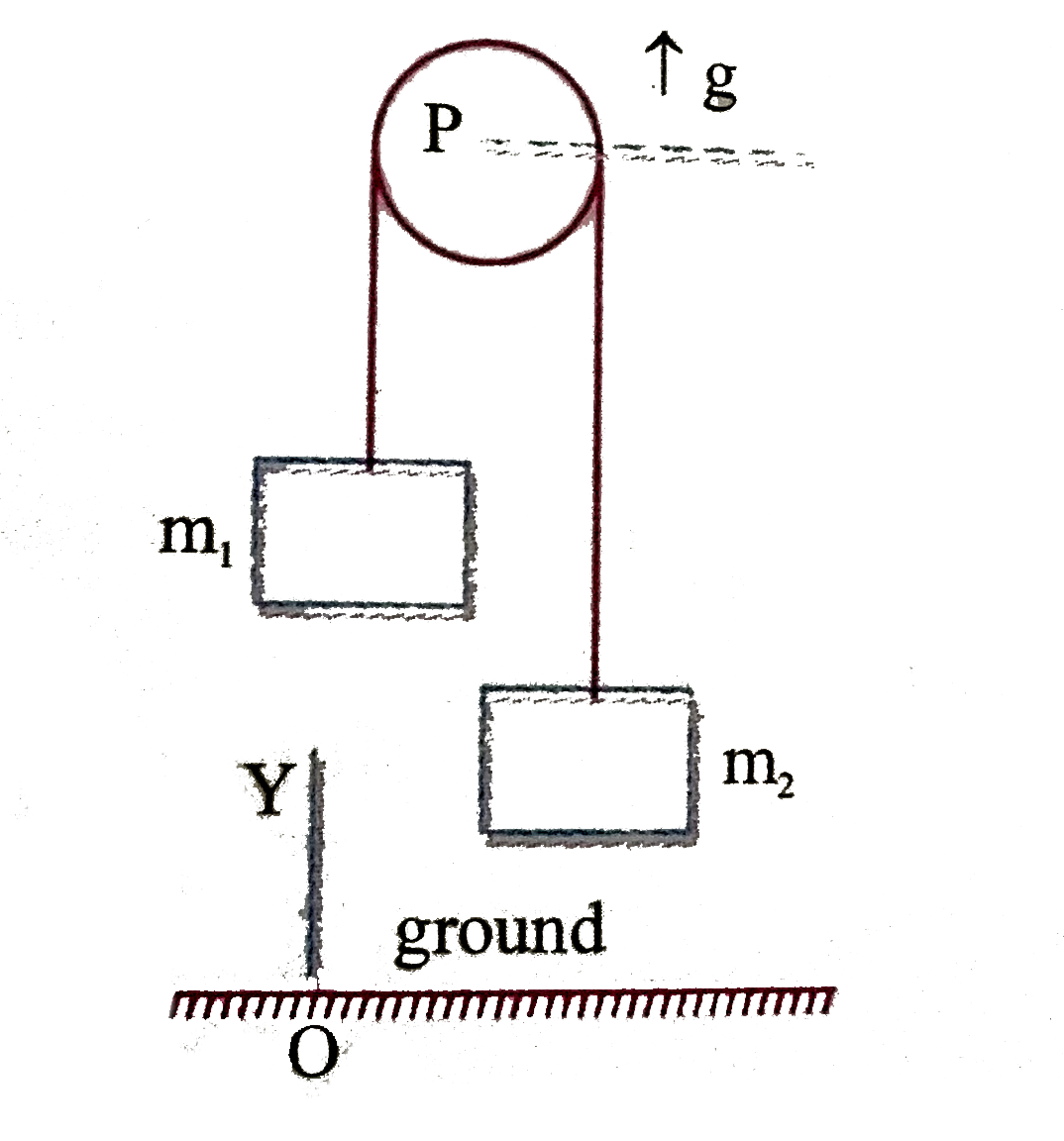 .ATension on the string is 4m1m2gm1+m2BTension on the string is 2m1m2gm1+m2CThe acceleration of mass m1 with respect to ground is 3m2−m1m1+m2g .DThe acceleration of mass m1 with respect to ground is 2(m2−m)m1+m2g
.ATension on the string is 4m1m2gm1+m2BTension on the string is 2m1m2gm1+m2CThe acceleration of mass m1 with respect to ground is 3m2−m1m1+m2g .DThe acceleration of mass m1 with respect to ground is 2(m2−m)m1+m2g - Question 2 - Select One
Two bodies of masses m1 and m2 are connected a light string which passes over a frictionless massless pulley. If the pulley is moving upward with uniform acceleration g2, then tension in the string will be
A3m1m2m1+m2gBm1+m24m1m2gC2m1m2m1+m2gDm1m2m1+m2g - Question 3 - Select One
Two masses m1 and m2 are connected by a light string passing over a smooth pulley. When set free m1 moves downward by 2 m in 2 s. The ratio m1/m2 is
A9/7B11/9C13/11D15/13
Two masses M and m are connected by a light inextensible string which passes over a small pulley as shown in the diagram. If the mass m is moving downward with a velocity v when the string makes an angle of 45∘ with the horizontal, find the total K.E. of the two masses. AsSigmae that the mass M moves horizontally.
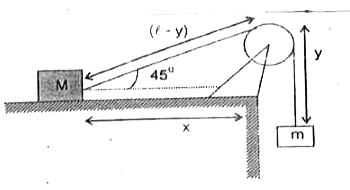 View Solution
View SolutionTwo blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
View SolutionTwo bodies of masses m1andm2(m2>m1) are connected by a light inextensible string which passes through a smooth fixed pulley. The instantaneous power delivered by an external agent to pull m1 with constant velocity v is :
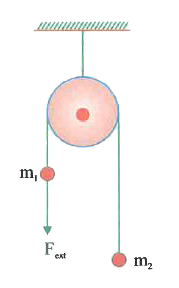 View Solution
View SolutionTwo blocks of mass m1andm2 are connected by light inextensible string passing over a smooth fixed pulleuy of negligible mass. The acceleration of the centre of mass of the system when blocks move under gravity is :
View SolutionTwo masses m1 and m2 are attached to a string which passes over a frictionless smooth pulley. When m1=10kg,m2=6kg, the acceleration of masses is
 View Solution
View Solution

