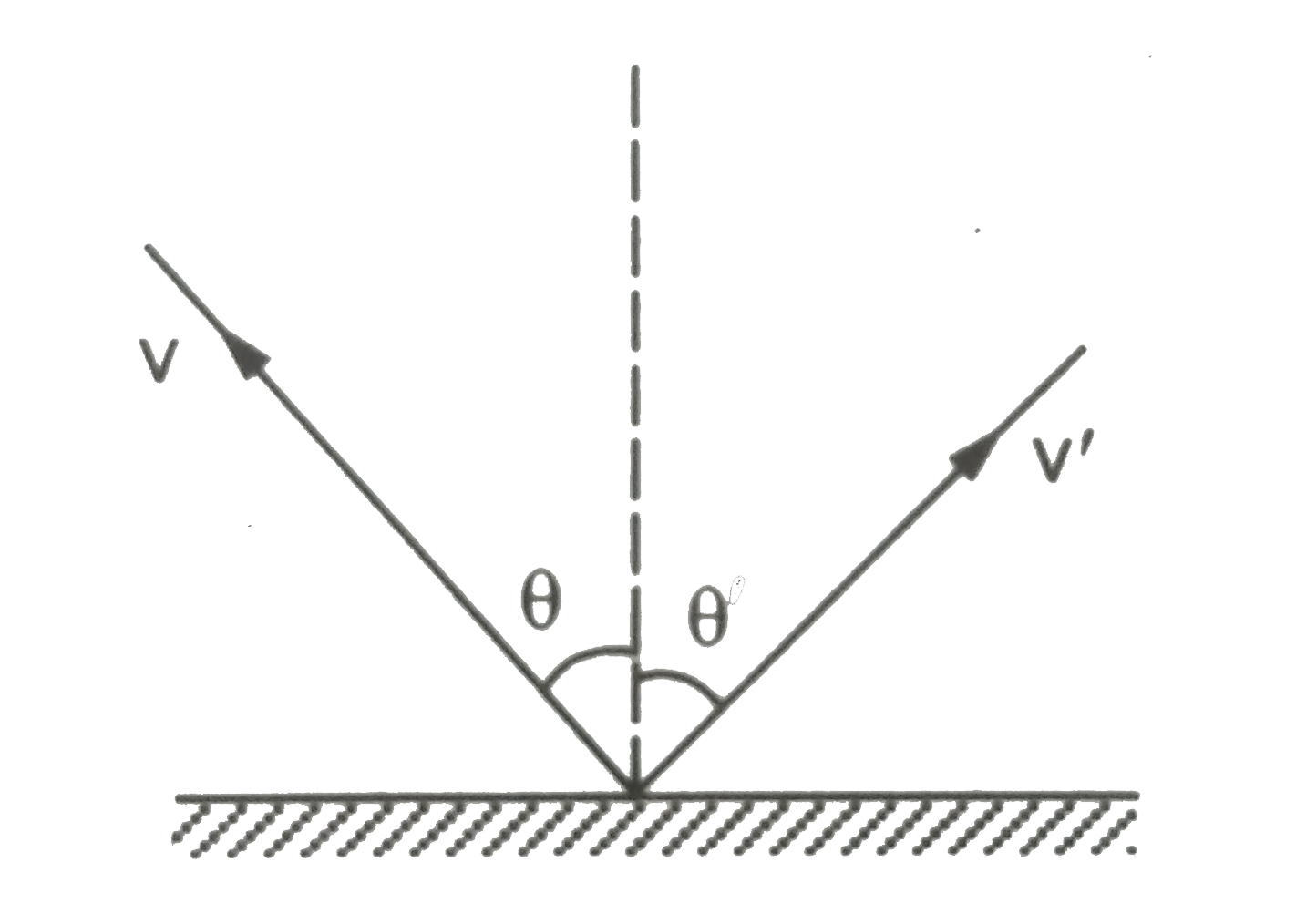
A ball of mass m hits the floor with a speed v0 making an angle of incidence α with the normal. The coefficient of restitution is e. find the speed of the reflected ball and the angle of reflection of the ball.
The component of velocity v0 along common tangent direction v0sinα will remain unchanged. Let v be the component along common normal direction after collision. Applying relative sped of separation =e× ( relative speed of approach) along common normal direction we get
v=ev0cosα
Thus, after collision components of velocity v' and v0sinα and ev0cosα.

∴v'=√(v0sinα)2+(ev0cosα)2
and tanβ=v0sinαev0cosα=tanαe
∴v'=v0 and β=α
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Solved Examples13videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.120videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
Similar Questions
A ball of mass m hits a floor with a speed v0 making an angle of incidence α with the normal. The coefficient of restitution is e. Find the speed of the reflected ball and the angle of reflection of the ball.
View SolutionA ball of a mass m hits the floor with as speed v making an angle of incidence θ with the normal. The coefficient of restitution is e. Find the speed of the reflected ball and the angle of reflection of the ball.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A particle of mass m strikes on ground with angle of incidence 45∘. If coefficient of restitution, e=1√2, find the velociy after impact and angle of reflection.
Atan−1(2)Btan−1(1√2)Ctan−1(√2)Dtan−1(12) - Question 2 - Select One
Two balls of masses 2m and m are moving with speed 2v0 and v0 towards each other. If the coefficient of restitution e=1/3 , the speed of balls , if collision is head - on
Av03,4v03B2v03,5v03C2v03,4v03Dv03,2v03 - Question 3 - Select One
A cricket ball of mass m strikes the bat with speed v normally and bounces back with speed v normally. The change in momentum of the ball is
A0BmvC2mvDdepends on the nature of collision
A particle of mass m strikes a smooth floor with speed u at angle of incidence θ with the normal. The coefficient of resultant is e. Find the magnitude and direction of velocity with which the particle rebounds. Also, find the impulse and loss in K.E.
View SolutionA particle of mass m strikes on ground with angle of incidence 45∘. If coefficient of restitution, e=1√2, find the velociy after impact and angle of reflection.
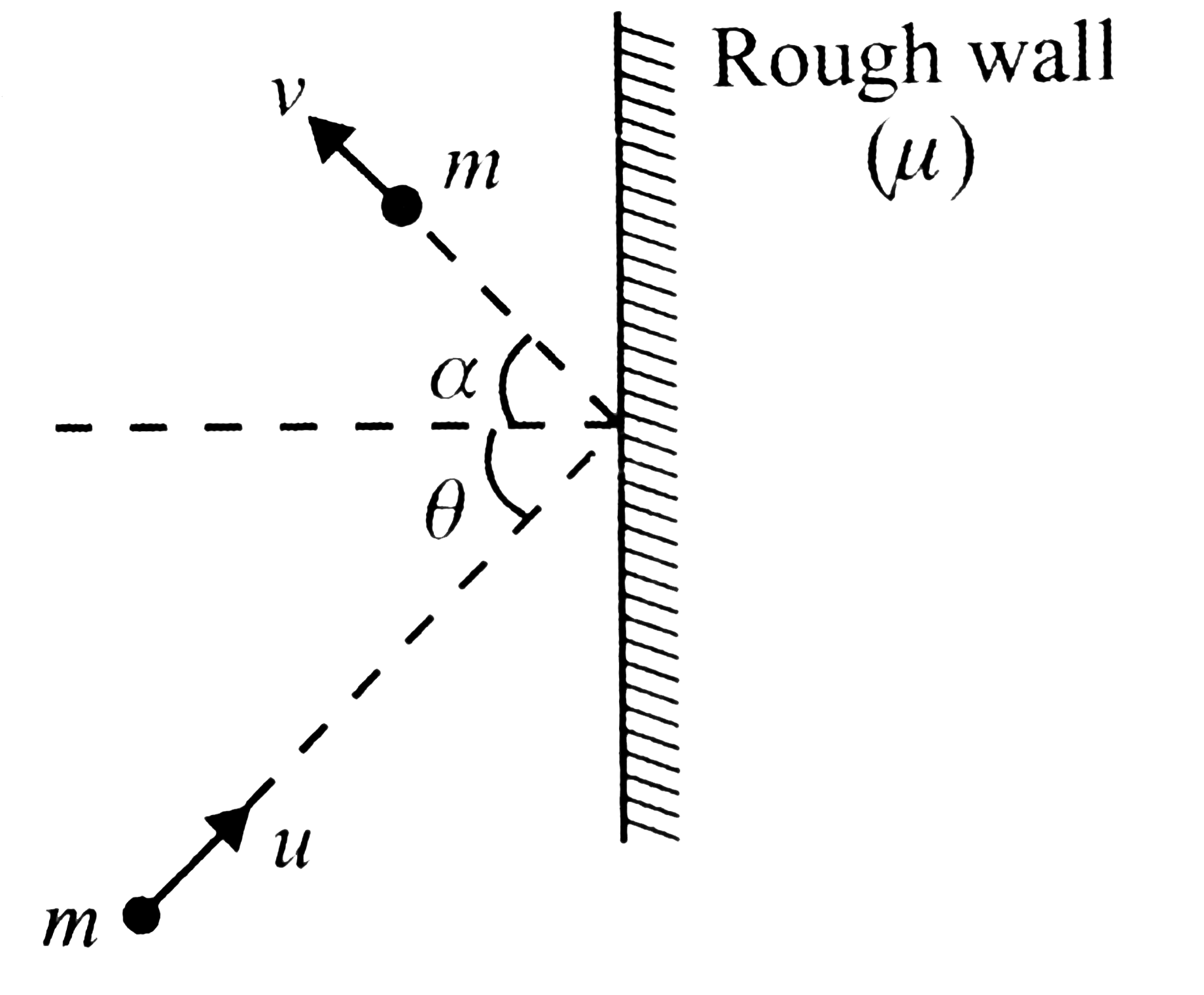
View SolutionA small ball of mass m collides with as rough wall having coefficient of friction μ at an angle θ with the normal to the wall. If after collision the ball moves with angle α with the normal to the wall and the coefficient of restitution is e, then find the reflected velocity v of the ball just after collision.
 View Solution
View SolutionA particle of mass m strikes a horizontal smooth floor with velocity u making an angle θ with the floor and rebound with velocity v making an angle θ with the floor. The coefficient of restitution between the particle and the floor is e. Then
View SolutionThe first ball of mass m moving with a velocity u collides head on with the second ball of mass m at rest. If the coefficient of restitution is e, the ratio of final velocity of the second ball to the initial velocity of the first ball is
View Solution

