A small particle of mass m is released from a height h on a large smooth sphere kept on a perfectly smooth surface as shown in the figure. Collision between particle and sphere is perfectly inelastic. Determine the velocities of particle and sphere after collision.
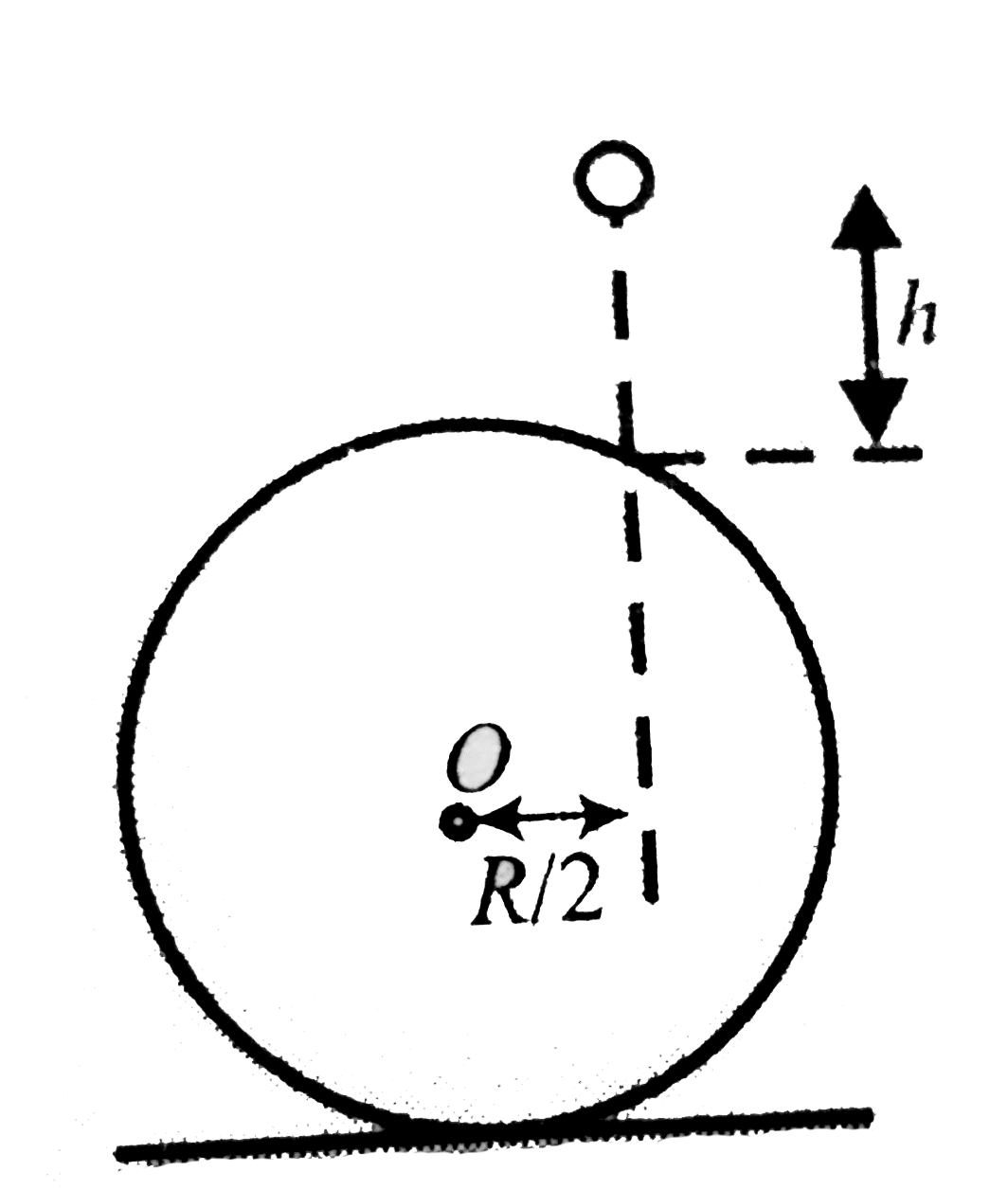
Collision takes lace between smooth bodies, therefore, tangential velocity of particle is unchanged.
vr=usinθ and u=√2gh
when sinθ=R2R=12 or θ=30∘
vt=u2 …………i

From conservation of momentum along x-axis,
Pi=Pf
0+0=MV+mvnsinθ+mvtcosθ..............iii
from the definitation of coefficient of restitution.
e=Vsinθ−(−vn)ucoshtη−0=0
[e=0, for a perfectly inelastic collision]
or, Vsinθ=−vn
vn=−V2 .............iii
On substitution expression for vn and vt in eqn ii we obtain
MV=m(−V2)12+m(u2)√32
(M+m4)V=mu√34
where u=√2gh or V=m√6gh(4M+m)
v=√v2n+v2t=
⎷6m2gh4(4M+m)2+gh2
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Subjective
23 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Single Correct
141 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.2
23 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A tiny ball of mass m is released from the state of rest over a large smooth sphere of mass M and radius R, which is at rest on a smooth horizontal surface. If the ball strikes the sphere perfectly inelastically, find their velocities after collision.
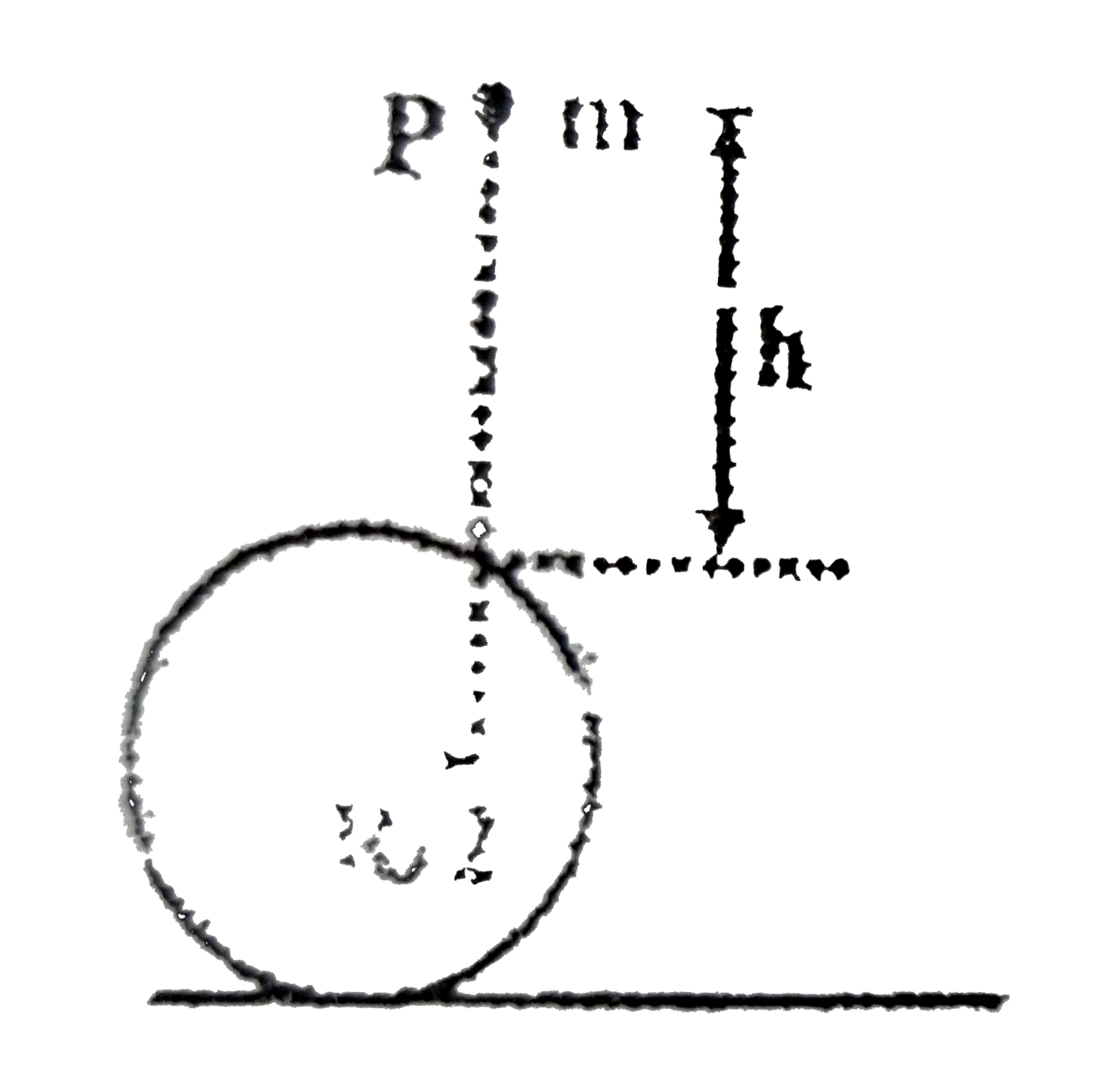
View SolutionA particle of mass m moving with velocity v0 collides with sphere of same mass at rest , as shown. If the surface of contact is smooth and the collision is elastic, find the velocities of particle and sphere after the collision.

View Solution
Knowledge Check
A particle of mass m is kept at the top of a smooth fixed sphere. It is given a horizontal velocity v then:
Ait will start moving along a circular path if v<√gRBit will start moving along a circular path if v>√gRCit will start moving along a parabolic path if v<√gRDit will start moving along a parabolic path if v>√gRTwo balls each of mass 'm' are moving with same velocity v on a smooth surface as shown in figure. If all collisions between the balls and balls with the wall are perfectly elastic, the possible number of collisions between the balls and wall together is
 A1B2C3DInfinity
A1B2C3DInfinityTwo balls each of mass 'm' are moving with same velocity v on a smooth surface as shown in figure. If all collisions between the balls and balls with the wall are perfectly elastic, the possible number of collisions between the balls and wall together is
 A1B2C3DInfinity
A1B2C3DInfinity
A particle of mass m strikes a disc of radius R and mass m with a speed u as shown in the figure. What is the speed of the particle just after the collision if the collision is perfectly inelastic ?
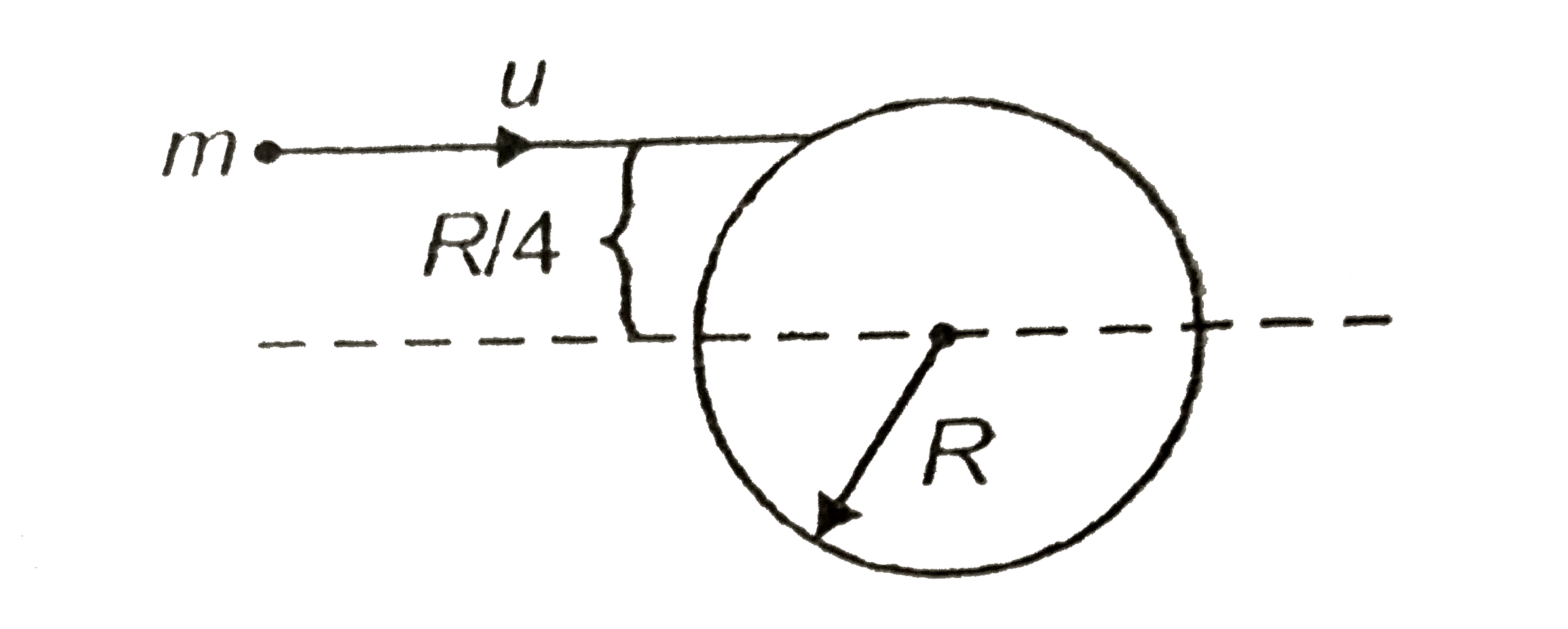
View SolutionA particle of mass m strikes a disc of radius R and mass m with a speed u as shown in the figure. What is the speed of the particle just after the collision if the collision is perfectly inelastic ?

View SolutionA particle of mass m strikes elastically with a disc of radius R, with a velocity →v as shown in the figure. If the mass of the disc is equal to that of the particle and the surface of the contact is smooth, find the velocity of the disc just after the collision.

View SolutionA particle is thrown upward with speed 20√2 m/s. It strikes the inclined surface as shown in the figure. Collision of particle and inclined surface is perfectly inelastic. What will be maximum height (in m) attained by the particle from the ground (g=10ms2)

View SolutionA sphere P of mass m and velocity vi undergoes an oblique and perfectly elastic collision with an identical sphere Q initially at rest. The angle θ between the velocities of the spheres after the collision shall be
View Solution
