A stationary light, smooth pulley can rotate without friction about a fixed horizontal axis. A light rope passes over the pulley. One end of the rope supports a ladder with man and the other end supports a counterweight of mass M. Mass of the man is m. initially, the centre of mass of the counterweight is at a height h from that of man as shown in Fig.
If the man starts to climb up the ladder slowly, calculate work done by him to reach his centre of mass in level with that of the counterweight.
The correct Answer is:W=MmghM−m
Mass of ladder =M−m, because net mass on both sides of string is same. Let in the given process, block M rises by height y, then ladder will come down by distance y and when man comes in the level of M, then height raised by man w.r.t ground will be h+y.
Now cenre of mass (man+ladder) system will be raised by y , then

y=m(h+y)+(M−m)(−y)2(M−m)
Now work done by man
W=total change in potential energy of system
⇒W=Mgy+mg(h+y)−(M−m)gy
Put the values of y and solve to get W=MmghM−m
Topper's Solved these Questions
- CENTRE OF MASSBook:CENGAGE PHYSICSChapter:CENTRE OF MASSExercise:Single Correct
Explore 141 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICSChapter:CENTRE OF MASSExercise:Multiple Correct
Explore 25 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICSChapter:CENTRE OF MASSExercise:Exercise 1.3
Explore 24 Videos
- CALORIMETRYBook:CENGAGE PHYSICSChapter:CALORIMETRYExercise:Solved Example
Explore 13 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
Similar Questions
A stationary pulley carries a rope whose one end supports a ladder with a man and the other end the counterweight of mass M. The man of mass m climbs up a distance l with respect to the ladder and then stops. Neglecting the mass of the rope and the friction in the pulley axle, find the displacement I of the centre of inertia of this system.
View SolutionA stationary pulley carries a rope whose one end supports a ladder with a man and the other end the counterweight of mass M. The man of mass m climbs up a distance I′ with respect to the ladder and then stops. Neglecting the mass of the rope and the friction in the pulley axle, find the displacement I of the centre of inertia of this system.
View Solution
Knowledge Check
A stationary pulley carries a rope whose one end supports a ladder with a man and the other end the counterweight of mass M. The man of mass m climbs up a distance l′ with respect to the ladder and then stops. Neglecting the mass of the rope and the friction in the pulley axle, find the displacement I of the centre of inertia of this system.
AmlM+mBml2MCmlM+2mDml2M+mA man of mass m stands on a frame of mass M. He pulls on a light rope, which passes over a pulley. The other end of the rope is attached to the frame. For the system to be in equilibrium, what force must the man exert on the rope?
 A(M+m)g2B(M+m)gC(M−m)gD(M+2m)g
A(M+m)g2B(M+m)gC(M−m)gD(M+2m)g
A man of mass m is suspended in air by holding the rope of a ballon of mass M. As the man climbs up the rope, the ballon

View SolutionA man of mass m is suspended in air by holding the rope of a ballon of mass M. As the man climbs up the rope, the ballon

View SolutionA man of mass m is suspended in air by holding the rope of a ballon of mass M. As the man climbs up the rope, the ballon

View SolutionA man of mass m stands on a frame of mass M. He pulls on a light rope, which passes over a pulley. The other end of the rope is attached to the frame. For the system to be in equilibrium, what force must the man exert on the rope?

View Solution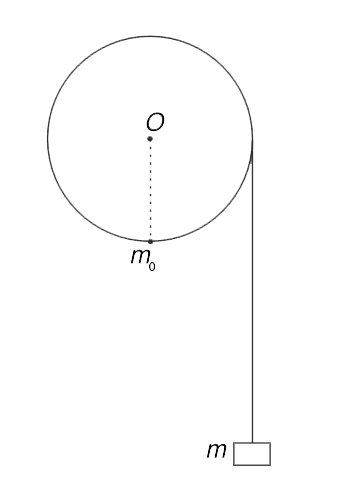
A uniform disc shaped pulley is free to rotate about a horizontal axis passing through the centre of the pulley. A light thread is tightly wrapped over it and supports a mass m at one of its end. A small particle of mass m0=2m is stuck at the lowest point of the disc and the system is released from rest. Will the particle of mass m0 climb to the top of the pulley?
View SolutionA rope thrown over a pulley has a ladder with a man of mass m on one of its ends and a counter balancing mass M on its other end. The man climbs with a velocity vr relative to ladder. Ignoring the masses of the pulley and the rope as well as the friction on the pulley axis, the velocity of the centre of mass of this system is:
View Solution
