An isolated smooth ring of mass M = 2m with two small beads each of mass m is as shown in the figure. Initially both the beads are at diametrically opposite points and have velocity v0 (for each) in same direction. The speed of the beads just before they collide for the first time is (complete system is placed on a smooth horizontal surface and assume each point of ring is touching the surface)

V0
2√3V0
V02
√32V0
The correct Answer is:D
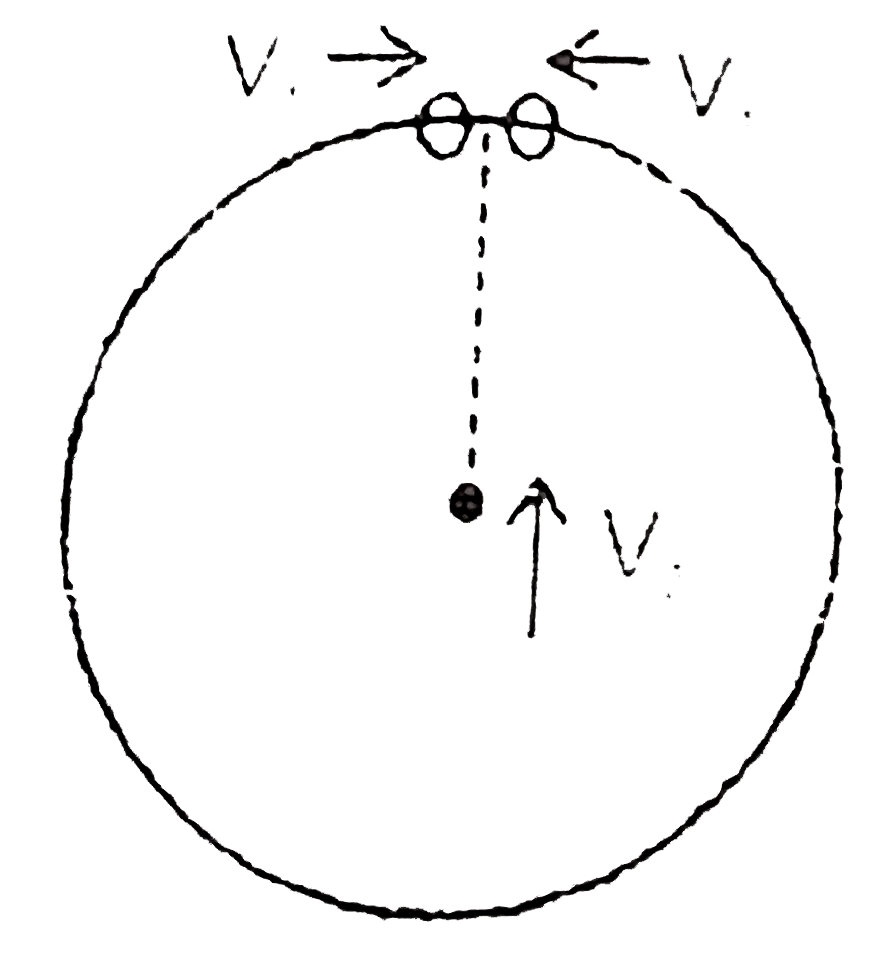
Just before the collision, situation is as shwon
Let the beads have velocity V1 .w.r.t. the ring and the ring has velocity V2.
Then, by momentum conservation 2mv0=(M+2m)V2
⇒V2=V02 …(i)
By mechanical energy conservation 12(2m)V20=122mv2+122m(V02)2
where v= velocity of beads .w.r.t. ground
So, V=√32V0
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.659videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.6620videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.639videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)21videos
CURRENT ELECTRICITY
- BOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
Similar Questions
A block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released
 View Solution
View SolutionTwo identical beads each of mass 'm' can slide freely on a ring of mass M lying on smooth horizontal surface. The masses are brought to diametrically opposite positions and both are imparted with same tangential speed v in same direction. Find the kinetic energy of the ring when beads are about to collide.
View Solution
Knowledge Check
- Question 1 - Select One
A hollow hemisphere of mass 4m is placed as shown in figure . Two point masses m each are fixed to it at points P and Q on diametrically opposite points. The position of center of mass of the system is
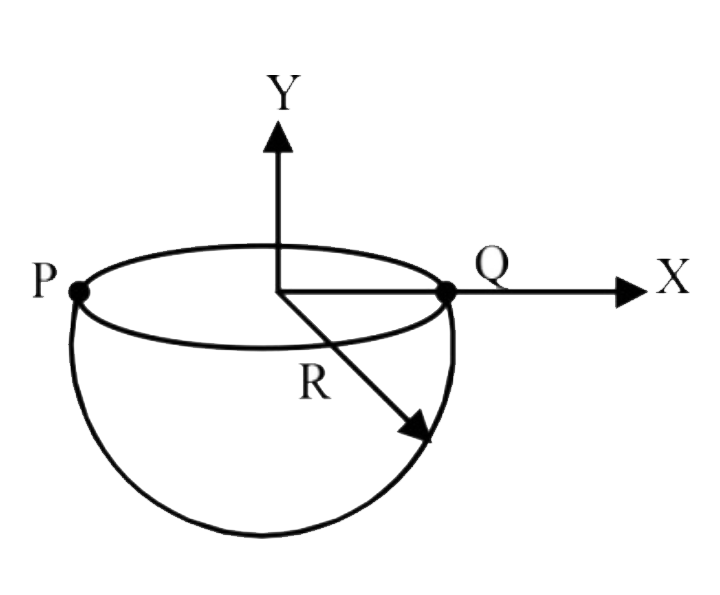 A(0,−R2)B(0,−R3)C(0,−2R3)D(0,−R4)
A(0,−R2)B(0,−R3)C(0,−2R3)D(0,−R4) - Question 2 - Select One or More
Four blocks each of mass M connected by a massless strings are pulled by a force F on a smooth horizontal surface, as shown in figure.
 AT3=14FBT2=12FCT1=34FDT1=T2=T3=12F
AT3=14FBT2=12FCT1=34FDT1=T2=T3=12F - Question 3 - Select One
A circular disc of mass M and radius R is rotating with angular velocity ω . If two small spheres each of mass m are gently attached to two diametrically opposite points on the edge of the disc, then the new angular velocity of the disc will be
A(M+4mM)ωB(MM+4m)ωC(M+mM)ωD(MM+2m)ω
Angular velocity of a ring is ω. If we put two masses each of mass m at the diametrically opposite points then the resultant angular velocity (m=mass of ring)
View SolutionAngular velocity of a ring is ω. If we put two masses each of mass m at the diametrically opposite points then the resultant angular velocity (m=mass of ring)
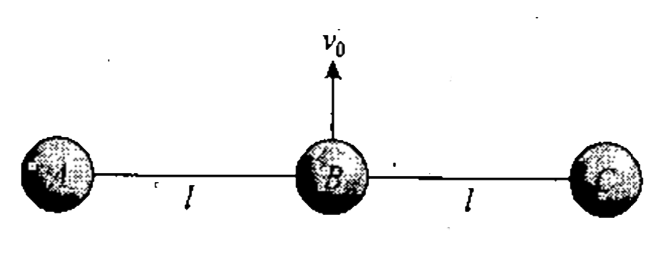
View SolutionThree identical balls eah of mass m=0.5 kg are connected with each other as shown in figure and rest over a smooth horizontal table At moment t=0, ball B is imparted a horizontal velocity v0=9ms−1 calculate velocity of A just before it collides with ball C.
 View Solution
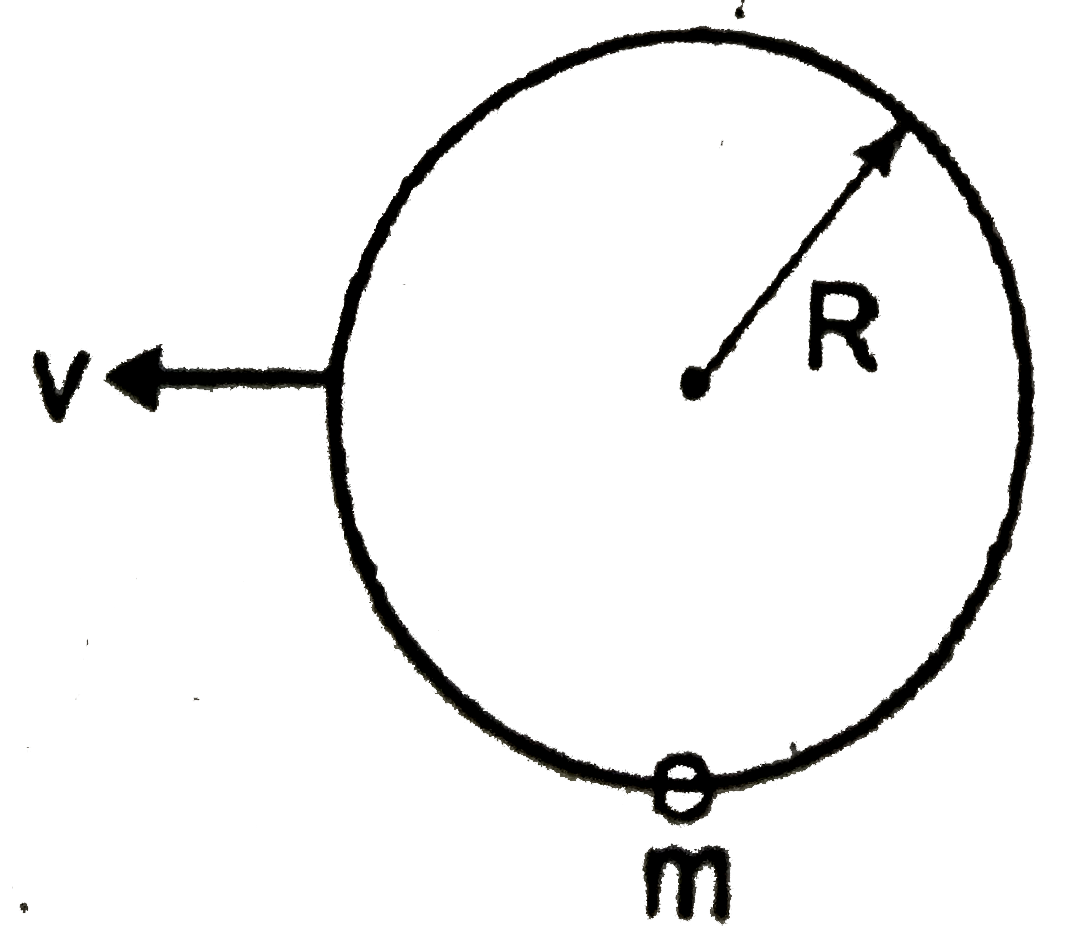
View SolutionA ring of radius R lies in vertical plane. A bead of mass 'm' can move along the ring without friction. Initially the bead is at rest the bottom most point on ring. The minimum horizontal speed v with which the ring must be pulled such that the bead completes the vertical circle.
 View Solution
View SolutionA smooth uniform rod of length L and mass M has two identical beads of negligible size each of mass m which can slide freely along the rod. Initially the two beads are at the centre of the rod and the system is rotating with an angular velocity ω0 about an axis perpendicular to the rod and passing through the midpoint of the rod. There are no external forces. When the beads reach the ends of the rod, the angular velocity of the system is ......
 View Solution
View Solution

