A horizontal frictionless rod is threaded through a bead of mass m. The length of the cart is L and the radius of the bead, r, is very small in comparison with L(r<<L). Initially at (t=0) the bead is at the right edge of the cart. The can is struck and as a result, it moves with velocity v0 towards right. When the bead collides with the cart's walls, the collisions are always completely elastic.
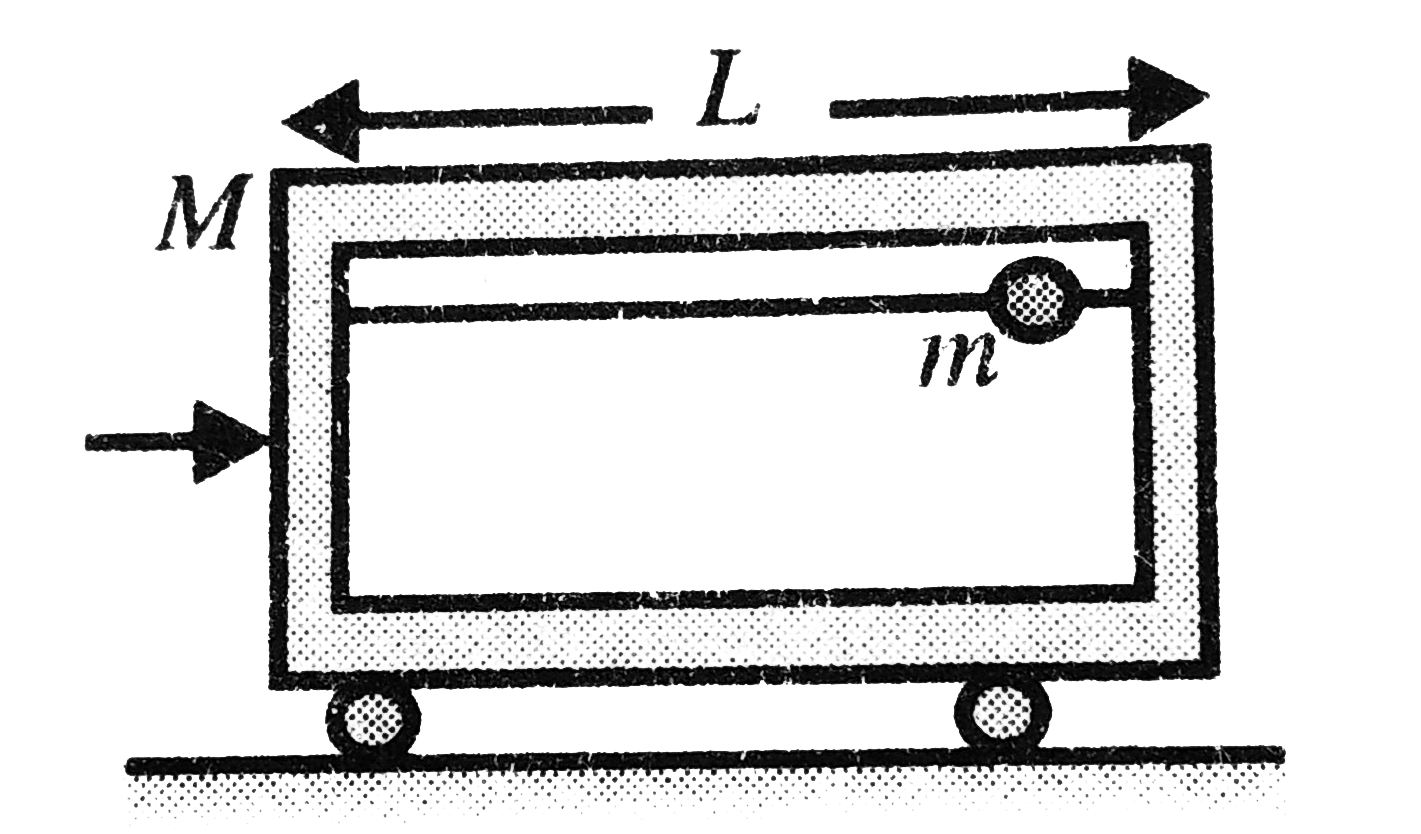
What is the velocity of the cart just after the first collision?
−mv0m+M
Mv0m+M
M−mM+mv0
2Mm+Mv0
The correct Answer is:C

Mv0=Mv1+mv2…………i
v2−v1v0=………..ii
Solve to get v1=M−mM+mv0
v2=2Mm+Mv0
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Integer16videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Fill In The Blanks2videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning2videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
Similar Questions
A bullet is fired on a fixed target. It penetrates inside the target through distance d=3.75cm and then stops. mass of the bullet is m=1kg and of the target is M=4kg. Now an identical bullet moving with the same velocity is fired on the identical target which is placed at rest on a frictionless horizontal surface. Then find the distance (in cm) to which the bullet will penetrate inside the target?
03:00View SolutionA particle of mass 4 m which is at rest explodes into three fragments. Two of the fragments each of mass m are found to move with a speed v each in mutually perpendicular directions. The total energy released in the process of explosion is ............
03:00View SolutionStatement I: In a two-body collision, the momenta of the particles are equal and opposite to one another, before as well as after the collision when measured in the centre of mass frame.
Statement. II: The momentum of the system is zero from the centre of mass frame.10:57View SolutionA colorimeter contains 400g of water at a temperature of 5∘C. Then, 200g of water at a temperature of +10∘C and 400g of ice at a temperature of −60∘C are added. What is the final temperature of the contents of calorimeter?
Specific heat capacity of water −1000 cal/kg/K
Specific latent heat of fusion of ice =80×1000 cal/kg
Relative specific heat of ice =0.509:03View SolutionTo find the distance d over which a signal can be seen clearly in foggy conditions, a railways-engineer uses dimensions and assumes that the distance depends on the mass density ρ of the fog, intensity (power/area) S of the light from the signal and its frequency f. the engineer finds that d is proportional to S1/n. the value of n is
04:57View SolutionA horizontal frictionless rod is threaded through a bead of mass m . The length of the cart is L and the radius of the bead, r , is very small in comparison with L(r lt lt L) . Initially at ( t = 0 ) the bead is at the right edge of the cart. The can is struck and as a result, it moves with velocity v_(0) towards right. When the bead collides with the cart's walls, the collisions are always completely elastic. Velocity of bead just after the first collision is
04:31View SolutionA horizontal frictionless rod is threaded through a bead of mass m . The length of the cart is L and the radius of the bead, r , is very small in comparison with L(r lt lt L) . Initially at ( t = 0 ) the bead is at the right edge of the cart. The can is struck and as a result, it moves with velocity v_(0) towards right. When the bead collides with the cart's walls, the collisions are always completely elastic. The first collision takes place at time ti and the second collision takes place at time t_(2) . Find t_(2)-t_(1)
View SolutionTwo beads of mass 2m and m , connected by a rod of length l and of negligible mass are free to move in a smooth vertical circular wire frame of radius l as shown. Initially the system is held in horizontal position ( Refer figure ) If the rod is replaced by a massless string of length l and the system is released when the string is horizontal then :
06:41View SolutionA bead can slide on asmooth straight wire and a particle of mass m attached to the bead by a light string of length L. The particle is held in contact with the wire and with the string taut and is then let fall. If the bead has mass 2m then when the string makes an angle theta with the wire, the bead will have slipped a dsitance.
02:29View SolutionA bead is connected with a fixed disc of radius R by an inextensible massless string in a smooth horizontal plane. If the bead is pushed with a velocity v_(0) prependicular to the string, the bead moves in a curve and consequently collapses on the disc. Then
03:38View SolutionA bead moves along a straight horizontal wire of length L, starting from the left end with velocity v0. Its retardation is proportional to the distance that remains to the right end of the wire. Find the initial retardation (at left end of the wire) if the bead reaches the right end of the wire with a velocity v02.
06:10View SolutionA rigid mass less rod of length L is rotating in a vertical plane about a horizontal axis passing through one of its ends. At the other end of the rod there is a mass less metal plate welded to the rod. This plate supports a heavy small bead that can slide on the rod without friction. Just above the bead there is another identical metal plate welded to the rod. The bead remains confined between the plates. The gap between the plates is negligible compared to L. The angular speed of the rod when the bead is at lowest position of the circle is ω=2√gL. How many times a clink of the bead hitting a metal plate is heard during one full rotation of the rod ?
 06:08View Solution
06:08View SolutionA thin insulating wire is stretched·along the diameter of an. insulated circular hoop of radius R. A small bead of mass m and charge-q is threaded onto the wire. Two small identical charges are tied to the hoop at points opposite to each other, so that the diameter passing through them is perpendicular to the thread as shown in figure. The bead is released at a point which.is located at a distance x0 from the centre of the hoop. Assume that x0<<R.
(a) What is the resultant force acting on the charged bead?
(b) Describe the motion of the bead after it is released X
(c) Use the assumption that xR<<1 to obtain an approximate equation of motion, and find the displacement and velocity of the bead as functions of time
(d) When will the velocity of the bead will bcome zero for the first time?
 02:08View Solution
02:08View SolutionA bead of mass 5 kg is free to slide on the horizontal rod AB. They are connected to two identical springs of natural length h ms. As shown. If initially bead was at O & M is vertically below L then, velocity of bead at point N will be :
 01:40View Solution
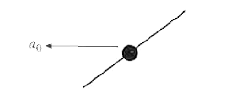
01:40View SolutionA bead of mass m moves on a rod without friction. Initially the bead is at the middle of the rod and the rod moves translationally in a vertical plane with an acceleration a0 in a direction forming angle θ with the horizontal as shown in the given figure. The acceleration of bead with respect to rod is
 03:31View Solution
03:31View Solution

