A uniform solid cylinder of mass m rests on two horizontal planks as shown in Fig. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically up with a force F. What is the maximum magnitude of the force F which still does not bring about any sliding of the cylinder, if the coefficient of friction between the cylinder and the planks is equal to μ. What is the maximum acceleration of the axis of the cylinder?
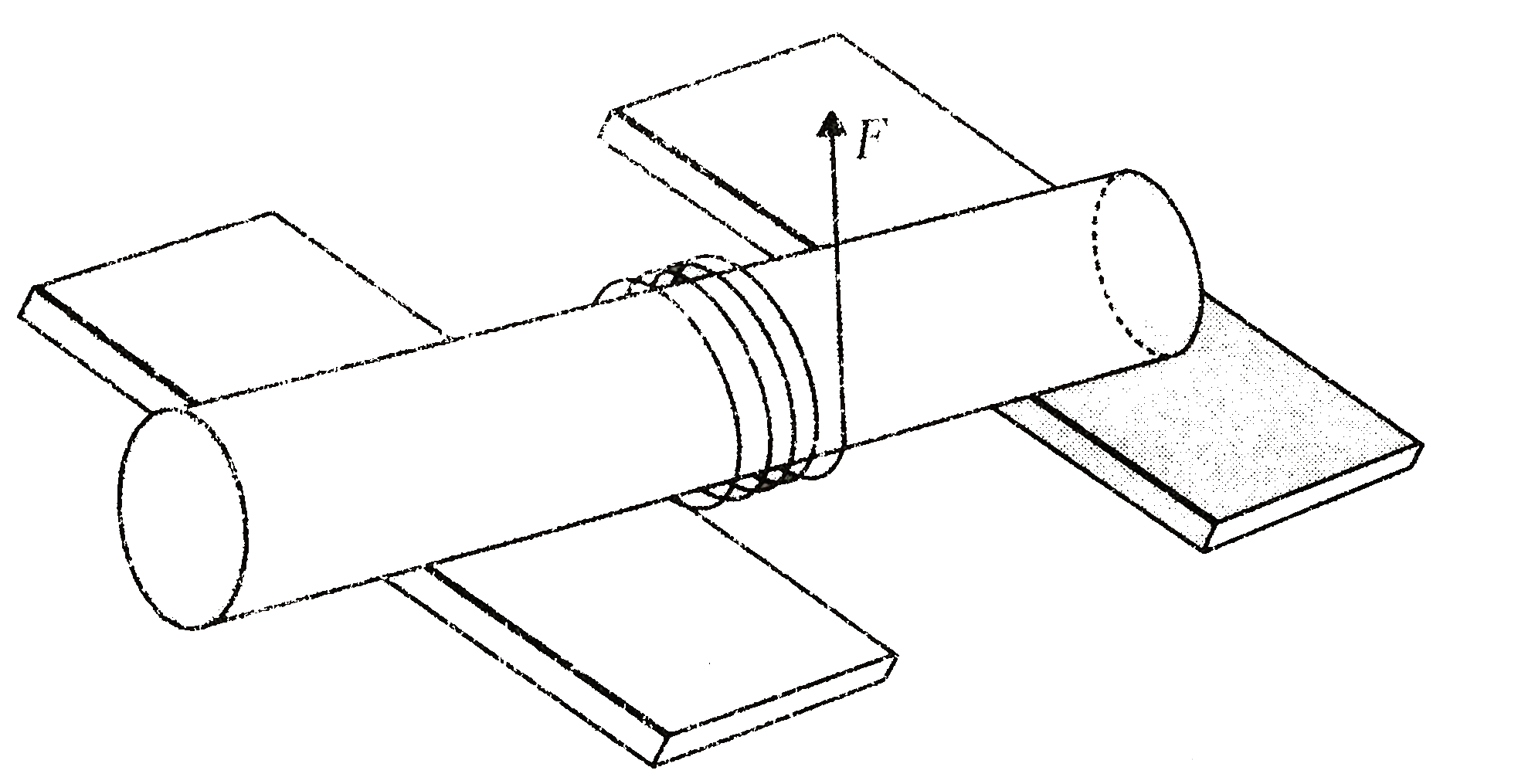
As the force F is applied the cylinder tends to rotate along anticlockwise direction with the point of contact C tending to move to the right. Hence, friction acts along the left (as shown in figure) If α is the angular acceleration of the cylinder then from τ=Iα we have
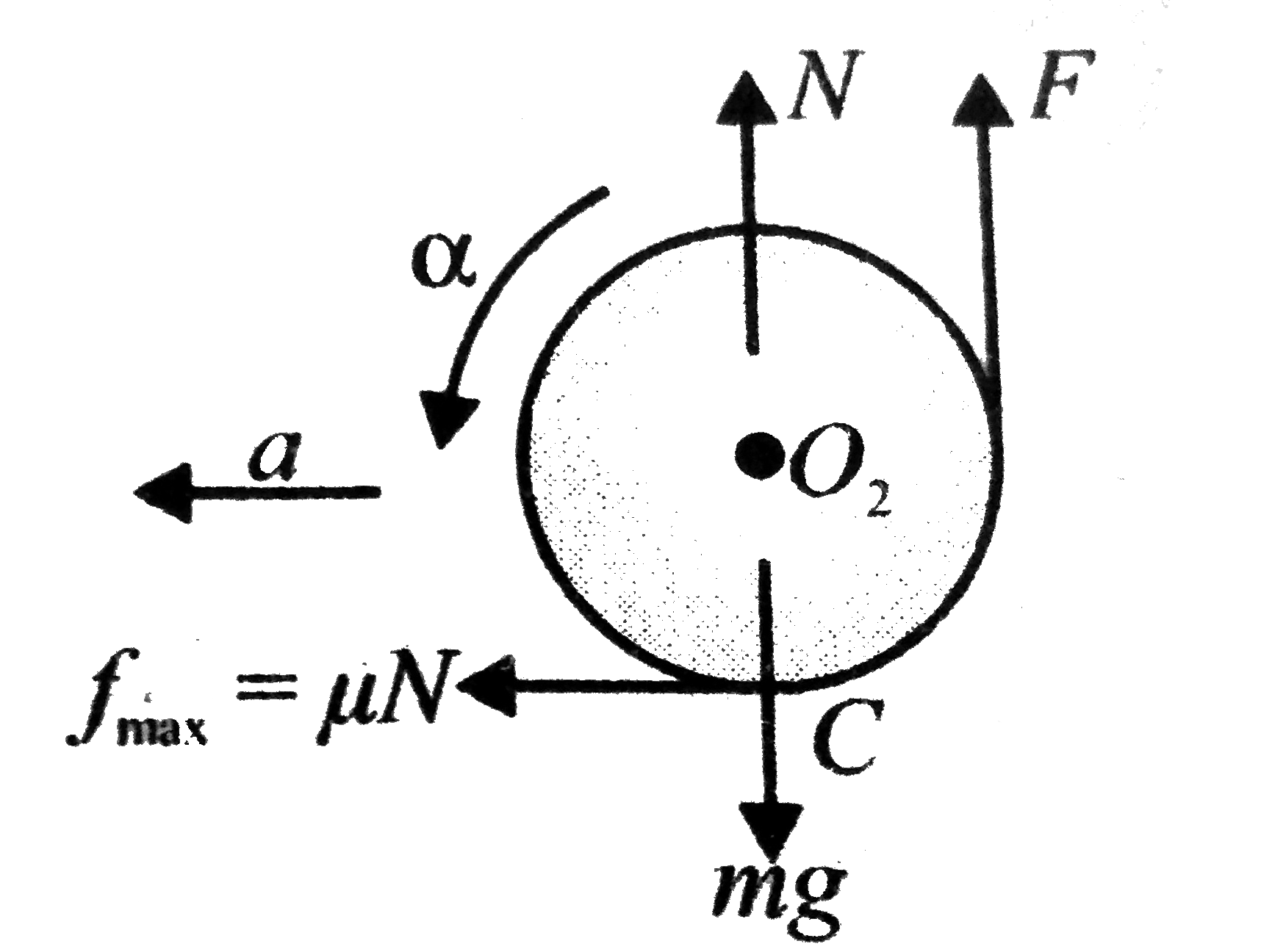
r(F−r)=(mr2/2)α...i
If a is the linear acceleratioin of the cylinder's CM, then from F=ma we have
f=ma........ii
For pure rolling,
a=αr............iii
Dividing Eq i by eqn ii we get
(F−f)f=rα2a=12
⇒F=(3f2)⇒Fmax=(32)fmax
[fmax=μN⇒μ(mg−F)]
⇒Fmax=3μ2[m≡LFmax]=3μmg2+3μ
from eq ii
a=fm
⇒amax=fmaxm=23mFmax=23m(3μmg2+3μ)=2μg2+3μ
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.4
13 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective
19 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.2
13 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A uniform solid cylinder of mass m rests on two horizontal planks. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically down with a constant force F(figure).
Find the maximum magnitude of the force F which still does not bring about any sliding of the cylinder, if the coefficient of friction between the cylinder and the planks is equal to k. What is the acceleration wmax of the axis of the cylinder rolling down the inclined plane?

View SolutionA uniform solid cylinder of mass m rests on two horizontal planks. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically down with a constant force F.
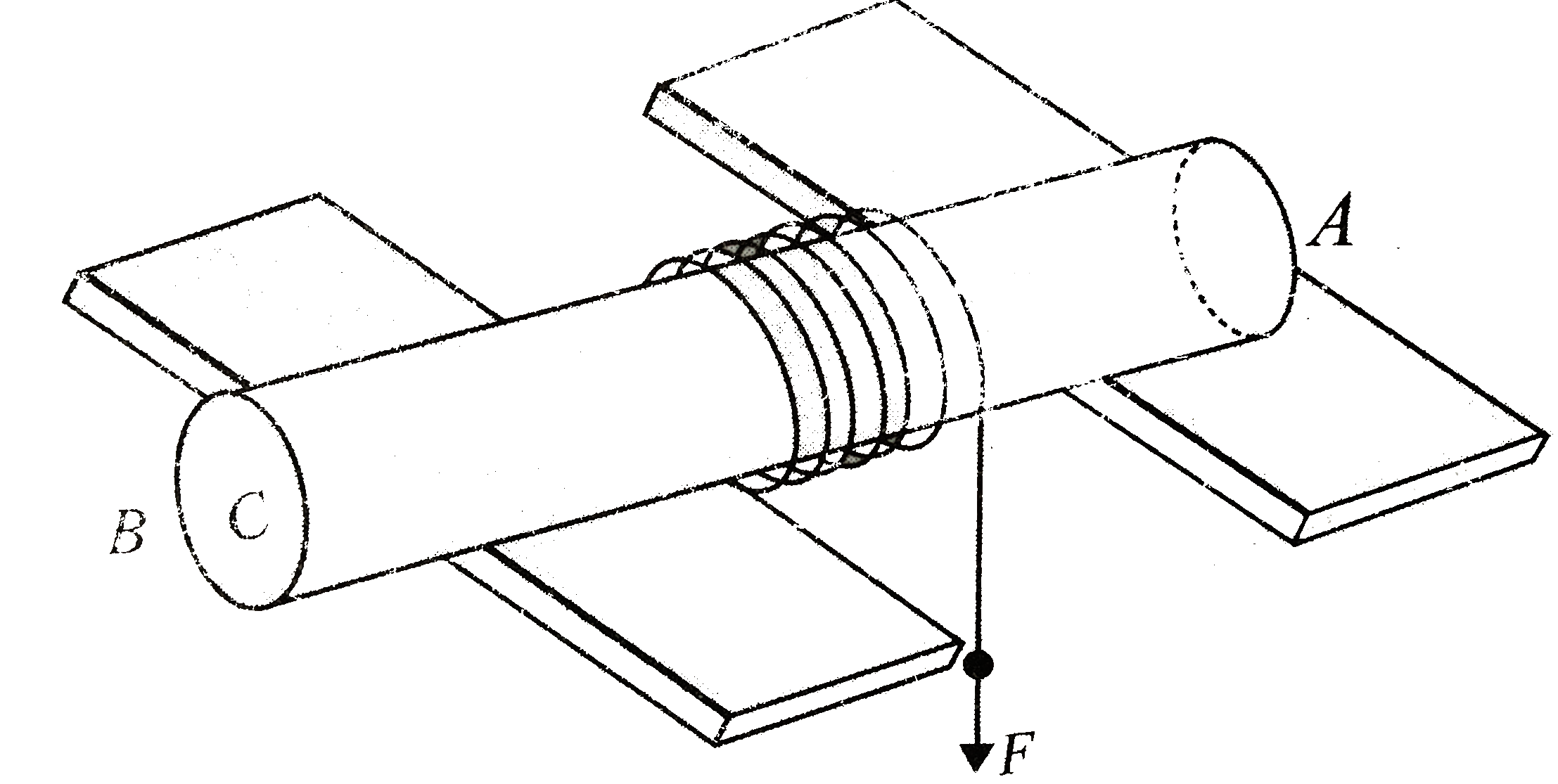
Find the maximum magnitude of the force F which may be applied without bringing about any sliding of the cylinder, if the coefficient of friction between the plank and the cylinder is equal to μ. What is the maximum acceleration of the centre of mass over the planks?
View Solution
Knowledge Check
A uniform cylinder of mass m rests on two rough horizontal planks. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically down with a constant force F
ASince horizontal acceleration is provided by the friction acting on the cylinder, its translation kinetic energy (12mv2) is equal to work done by this friction,BSince moment about instantaneous axis of rotation is produced by force F. kinetic energy (12Iω2) is equal to work done by F where I is moment of inertia about the instantaneous axis of rotation and ω is the-angular velocity.CSince cylinder is moving, energy is lost against friction.DWork done by F+ work done by friction on cylinder =totalKE of the cylinder.
A uniform solid cylinder having mass M and radius R is pulled by a horiozntal force F acting through the center as shown. The cylinder rolls to the right without slipping. What is the magnitude of the force of friction between the cylinder and the ground?AF/4BF/3CF/2D2F/3A rope is wound round a hollow cylinder of mass M and radius R. If the rope is pulled with a force F newton, then the angular acceleration of the cylinder will be
AMRFBMRFCRMFDFMR
A cylinder of mass 2kg and radius 10cm is held between two planks as shown in Fig. Calculate KE of the cylinder when there is no slipping at any point.

View SolutionA cylinder of weight W and raidus R is to be raised onto a horizontal step of height h=R/3 as shown. A rope is wrapped around the cylinder and pulled horizontally. Assuming no slipping, find the minimum value of F to raise the cylinder.

View SolutionA solid cylinder of mass m is resting on fixed rough inclined plane with help of a thread. Find friction force between cylinder and inclined plane. (given μ=0.4)

View SolutionA rope is wound round a hollow cylinder of mass M and radius R. If the rope is pulled with a force F newton, then the angular acceleration of the cylinder will be
View SolutionA rope is wound round a hollow cylinder of mass 2 kg and radius 0.5 m. If the rope is pulled with a force of 80 N, the angular acceleration of the cylinder will be -
View Solution
