A solid sphere of mass M is placed on the top of a plank of the same mass, after giving an angular velocity ω0 at t=0. Find the velocity of the plank and the sphere when the sphere starts rolling:,

Step 1: Free body diagram
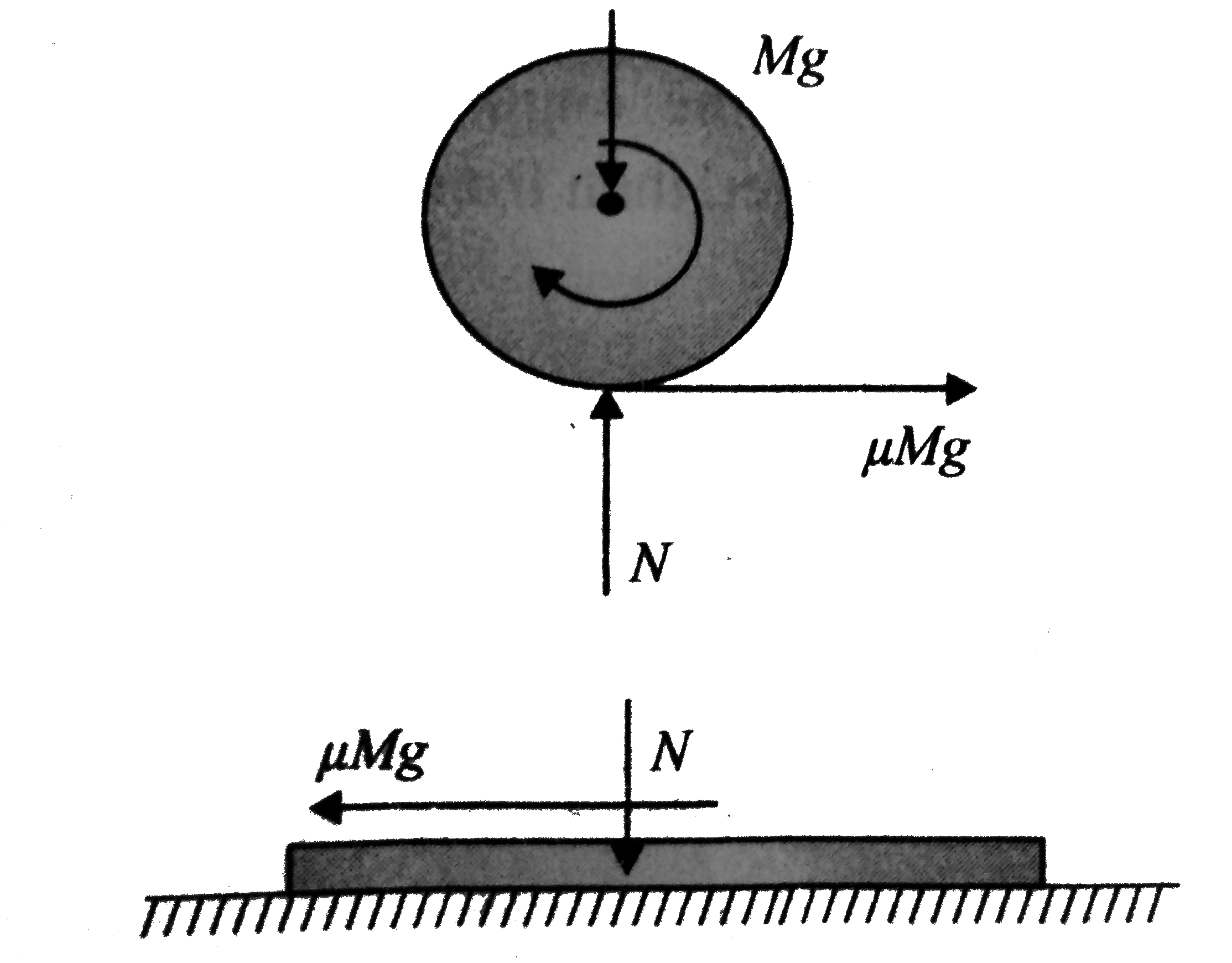
Step 2: Equation of motion,
μMg=MA⇒A=μg (backward)
(A will be positive)
sphere
μMg=MA⇒a=μg (forward)
(a will be positive)
Step: Torque equation
μMgR=(25MR2)α
α=52μgR (anticlockwise)
(it will be negative )
Step 4: constraint relation
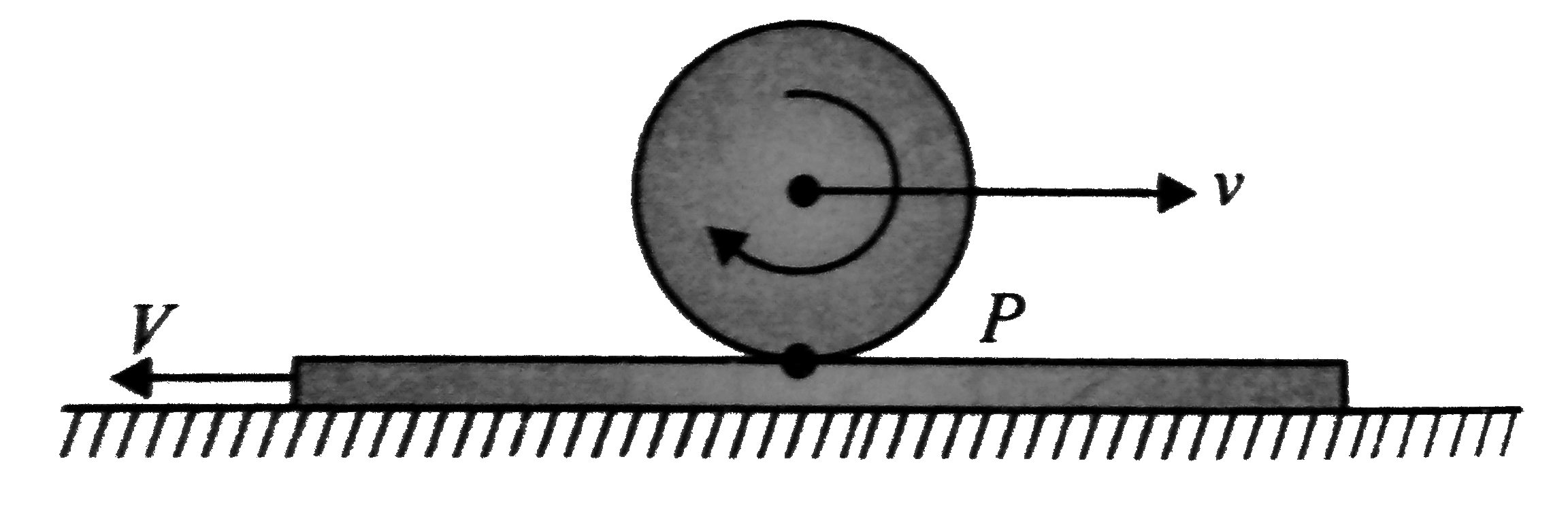
VP=V=ωR=v
(0+μ>)=(ω0−52μgRt)R−(0+μgt)
(2μgt+52μgt)=ω0R⇒9μt2=ω0R
⇒t−2ω0R9μg
Velocity of the plane when rolling starts
V=0+μgt
Vplank=μg×2ω0R9μg=29ω0R
velocity of the sphere when rolling starts
Vsphere=0+μgt=29ω0R
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.413videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective19videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.213videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A plank of mass M rests on a smooth horizontal plane. A sphere of mass m and radius r is placed on the rough upper surface of the plank and the plank is suddenly given a velocity v in the direction of its length. Find the time after which the sphere begins pure rolling, if the coefficient of friction between the plank and the sphere is μ and the plank is sufficiently long.
View SolutionA uniform solid sphere of radius R, rolling without sliding on a horizontal surface with an angular velocity ω0, meets a rough inclined plane of inclination θ=60∘. The sphere starts pure rolling up the plane with an angular velocity ω Find the value of ω.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.
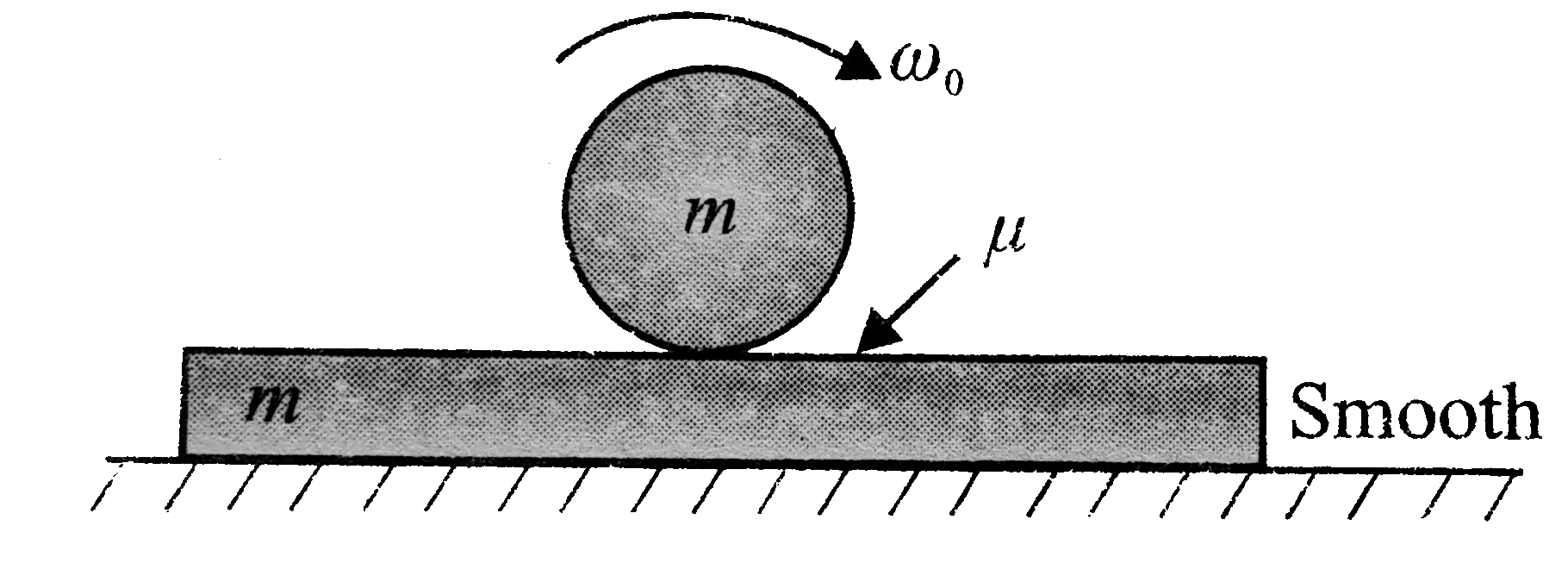
Find the velocity of the sphere after the pure rolling startsA2ω0r9Bω0r9Cω0r3D2ω0r3 - Question 2 - Select One
A long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the displacement of the plank till the sphere starts pure rolling.Aω20r281μgB227ω20r2μgC481ω20r2μgD281ω20r281μg - Question 3 - Select One
Assertion : A solid and a hollow sphere both of equal masses and radii are put on a rough surface after rotating with some angular velocity say ω0. Coefficient of friction for both the spheres and ground is same. Solid sphere will start pure rolling first
Reason : Radius of gyration of hollow sphere about an axis passing through its centre of mass is more.AIf both Assertion and Reason are correct and Reason is the correct explanation of AssertionBIf both Assertion and Reason are true but Reason is not the correct explanation of AssertionCIf Assertion is true but Reason is fasleDIf Assertion is false but Reason is true
A solid sphere of radius r and mass m rotates about an axis passing through its centre with angular velocity ω. Its K.E. Is
View Solution
solid sphere of radius r is gently placed on a rough horizontal ground with an initial angular speed ω0 and no linear velocity. If the coefficient of friction is μ, find the time t when the slipping stops. in addition state the linear velocity v and angular velocity ω at the end of slippingView SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.
Acceleration of centre of mass of sphere isView SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.

Force of friction between sphere and plank isView SolutionA small body of mass 'm' is placed at the top of a smooth sphere of radius 'R' placed on a horizontal surface as shown, Now the sphere is given a constant horizontal acceleration a0=g. The velocity of the body relative to the sphere at the moment when it loses contact with the sphere is
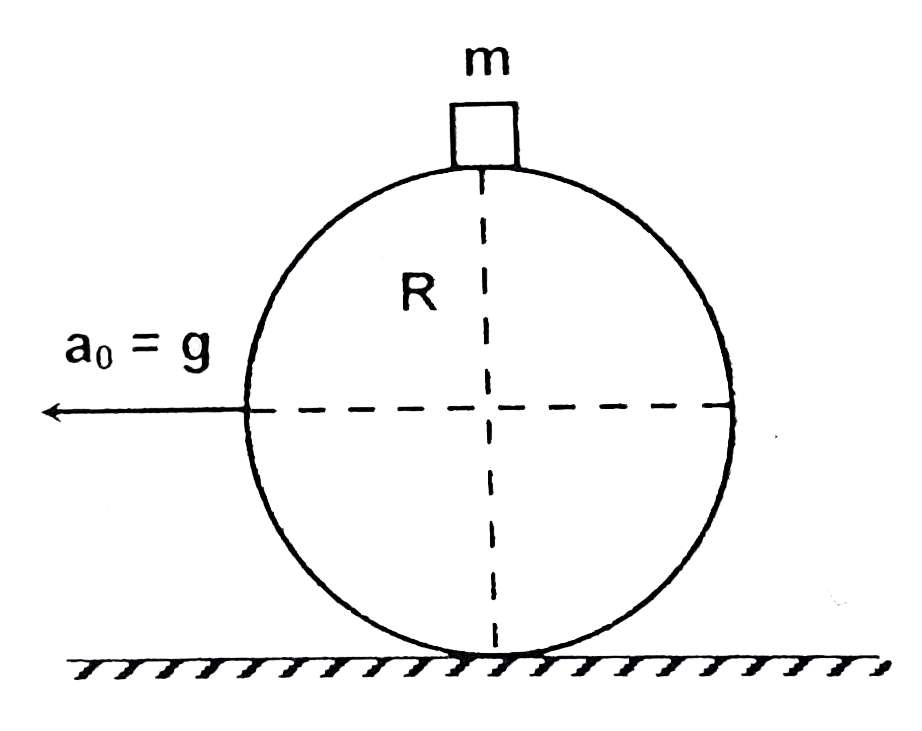 View Solution
View Solution

