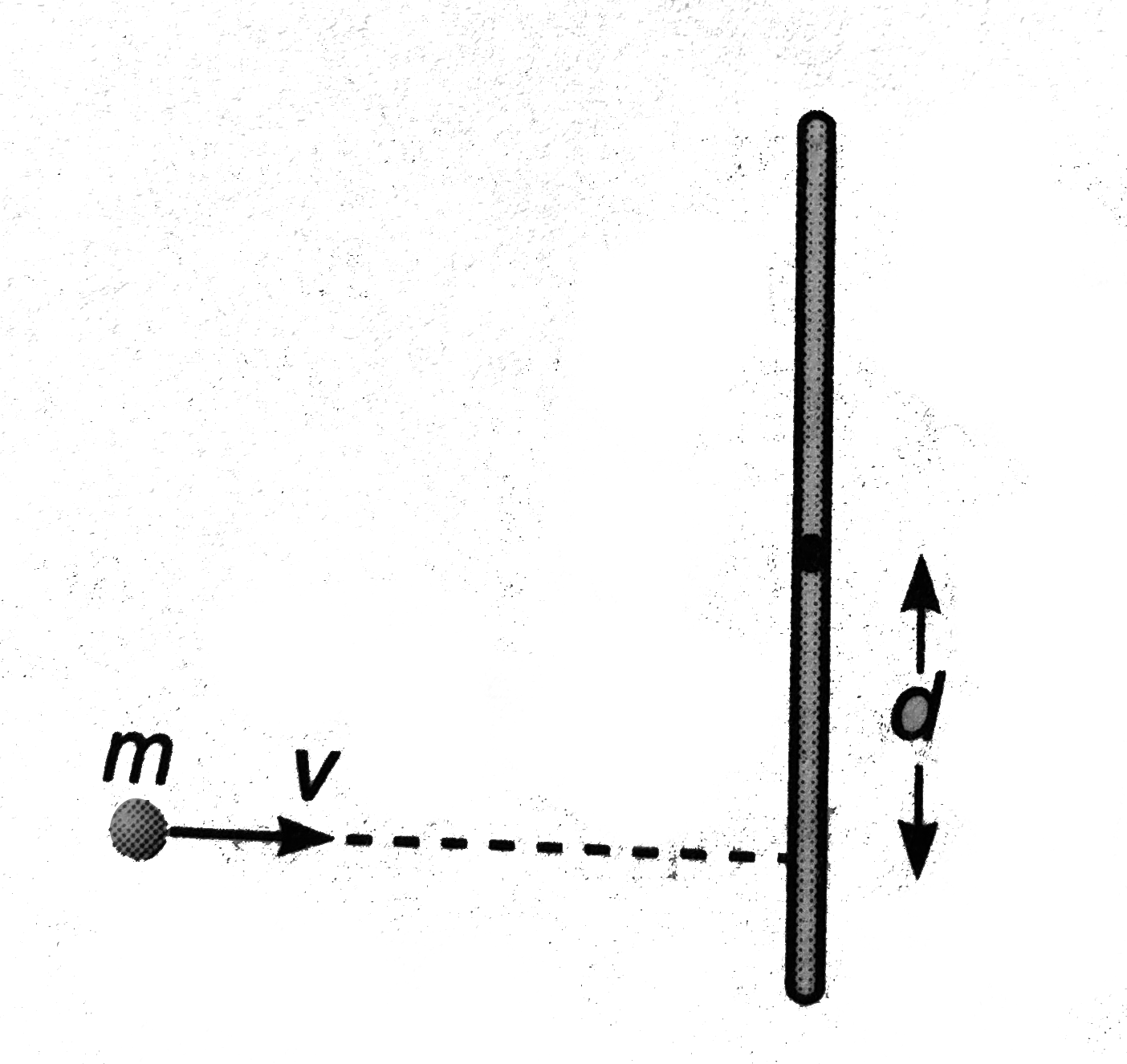
A stick of length l lies on horizontal table. It has a mass M and is free to move in any way on the table. A ball of mass m moving perpendicularly to the stick at a distance d from its centre with speed v collides elastically with it as shown in figure. What quantities are conserved in the collision ? what must be the mass of the ball, so that it remains at rest immediately after collision?

By conservation of linear momentum and angular momentum, we have
mv+0=m.0+MV⇒=V=mvM
and mvd=Iω⇒ω=mvdI=mvdML212
since collision is elastic, therefore
12mv2=12M(mvM)2+12(ML212)⎛⎜⎝mvdmL212⎞⎟⎠2
⇒m=ML2L2+12d2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective19videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Single Correct142videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.321videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A stick of length L and mass M lies on a frictionless horizontal surface on which it is free to move in any way. A ball of mass m moving with speed v collides elastically with the stick as shown in the figure. If after the collision the ball comes to rest, then what would be the mass of the ball?
 View Solution
View SolutionA meter stick of length l and mass M lies on a frictionlesss table. The stick is free to move in any way on the table. A hockey ball of mass m moving perpendicuarly to the mass of the ball so that it remains at rest immediately after the collision?
[Hint: Elastic collision means that kinetic energy is conserved in the process. Consider conservation of kinetic energy, conservation of angualr momentum and linear momentum, i.e., 12mv2 = (12Mv2'+12Iε2, mv12=Iε, mv=Mv′.
Eliminate v2' and w2 from the first with the help of the other two. Use the expression I=112MI2]View Solution
Knowledge Check
- Question 1 - Select One
A stick of length L and mass M lies on a frictionless horizontal surface on which it is free to move in any way. A ball of mass m moving with speed v collides elastically with the stick as shown in the figure. If after the collision the ball comes to rest, then what would be the mass of the ball?
 Am=2MBm=MCm=M/2Dm=M/4
Am=2MBm=MCm=M/2Dm=M/4 - Question 2 - Select One
A Stick of length L and mass M lies on a fnctionless horizontal surface on which it is free to move in any way. A ball of mass m moving with speed v collides elastically with the stick as shownin figure-5.115. If after the collision ball comes to rest, then what should be the mass of the ball ?
 Am=2MBm=MCm=M/2Dm=M/4
Am=2MBm=MCm=M/2Dm=M/4 - Question 3 - Select One
A ball A of mass M collides elastically with a similar ball B at rest as shown in figure. Initially velocity of ball A is u m/s. After collision,
 ASpeed of ball B is u sinθBVelocity of ball A is usin2θˆi+usinθcosθˆjCSpeed of ball A is ucosθDVelocityofballBisu cos theta sin theta hati + u cos^2 theta hatj
ASpeed of ball B is u sinθBVelocity of ball A is usin2θˆi+usinθcosθˆjCSpeed of ball A is ucosθDVelocityofballBisu cos theta sin theta hati + u cos^2 theta hatj
A uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View SolutionA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the angular momentum of the particle and of then about the centre of mass C before the collision.View SolutionA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the particle with respect to C before the collisionView SolutionA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the rod with respect to C before the collisionView SolutionA uniform stick of length l is mounted so as to rotate about a horizontal axis perpendicular to the stick and at a distance d from the centre of mass. The time period of small oscillation has a minimum value when d/l is
View Solution

