A thin uniform rod of length $l$ is initially at rest with respect to an inertial frame of reference. The rod is tapped at one end perpendicular to its length. How far the centre of mass translates while the rod completes one revolution about its centre of mass. Neglect gravitational effect.

Video Solution

Text Solution

Verified by Experts

Let $△ t$ be the duration of impact, then
$J = △ \to P$
or $J = (M v_{c} - 0)$ ….i

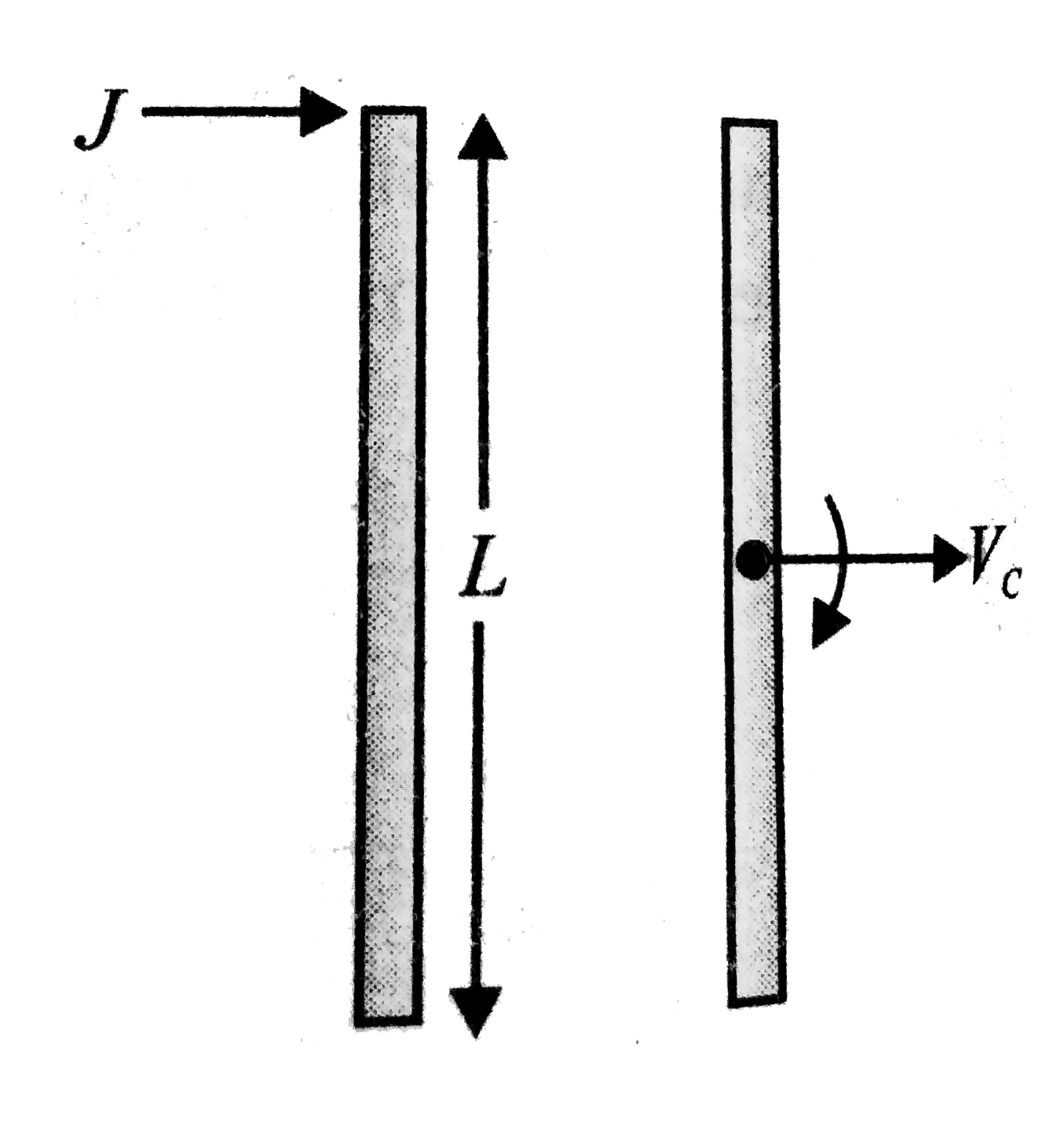
Angular impulse is equal to change in angular momentum
or $\frac{J l}{2} = (△ ω)$
$= I (ω - 0) = \frac{m l^{2}}{12} ω$ ……..ii
Dividing eqn in by eqn ii we get
$ω = \frac{6 v_{0}}{l}$
Let t be the time inwhich the rod rotates at angle $2 π$ then
$ω t = 2 π \Rightarrow t = \frac{π L}{3 v_{0}}$
Hence distance travelled by centre of mass $\Rightarrow x_{c} = \frac{l π}{3}$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If $l_{1}$ is the moment of inertia of a thin rod about an axis perpendicular to its length and passing through its centre of mass and $l_{2}$ is the moment of inertia (about central axis) of the ring formed by bending the rod, then the ratio of $I_{1}$ to $I_{2}$ is
A $l : l = 1 : 1$
B $l : l = π : 3$
C $l : l = π : 4$
D $l : l = 3 : 5$
Question 2 - Select One
A uniform rod of mass m and length l is rotating with constant angular velocity $ω$ about an axis which passes thorugh its one end and perpendicular to the length of rod. The area of cross section of the rod is A and its Young's modulus is y. Neglect gravity. The strain at the mid point of the rod is:
A $\frac{m n^{2} l}{8 A y}$
B $\frac{3 m ω^{2} l}{8 A y}$
C $\frac{3 m ω^{2} l}{4 A y}$
D $\frac{m ω}{4 A y}$
Question 3 - Select One
A light rod of length $l$ has two masses $m_{1}$ and $m_{2}$ attached to its two ends. The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is.
A $(m_{1} + m_{2}) l^{2}$
B $\sqrt{m_{1} m_{2}} l^{2}$
C $\frac{m_{1} m_{2}}{m_{1} + m_{2}} l^{2}$
D $\frac{m_{1} + m_{2}}{m_{1} m_{2}} l^{2}$

CENGAGE PHYSICS-RIGID BODY DYNAMICS 2-Exercise 3.4

Home
Ask Doubt
Profile