Two identical particles B and C each of mass 50g are connected by a light rod of length 30CM. Another particle A of same mass moving With a speed u=60CM/s strikes B, in a direction perpendicular to AB, and sticks to it. The whole process takes place on a smooth horizontal plane. Find the angular velocity ω of the system about its centre of mass, immediately after the impact.

Clearly, the centreof mass of the system (A+B+C) is at a distance of 10cm from along the rod
Initial angualr momentum
Li=mAvArA
=50×10−3×60×10−2×10×10−2
=3×10−3 S.I. unit
Moment of inertia about new centre of mass
I=(2×50×10−3)x(10×10−2)2+(50+10−3)×(20×10−2)2
=3×10−3 S.I. unit
From Li=Lf⇒Li=I.ω
⇒ω=Li=1rad/s
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective19videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Single Correct142videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.321videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
Two particles A and B, each of mass m, are connected by a light rod of length L lying on a smooth horizontal surface. A particle of mass m moving with speed v0 strikes to the end of rod and sticks to A as shown . Find
(a) the velocity of the center of mass,
(b) the angular velocity about the center of mass of system (A+B+ particle) and
(c) the linear speeds of A and B immediately after collision.
 View Solution
View SolutionA particle of mass 2m moving with velocity v strikes a stationary particle of mass 3m and sticks to it. The speed of the system will be
View Solution
Knowledge Check
- Question 1 - Select One
A uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the centre of mass C and the angular, velocity of the system about the centre of mass after the collision.A2mvM+m,3Mv(M+2m)LBMvM+m,6Mv(M+4m)LC2mvM+m,3Mv(M+4m)LDmvM+m,6Mv(M+4m)L - Question 2 - Select One
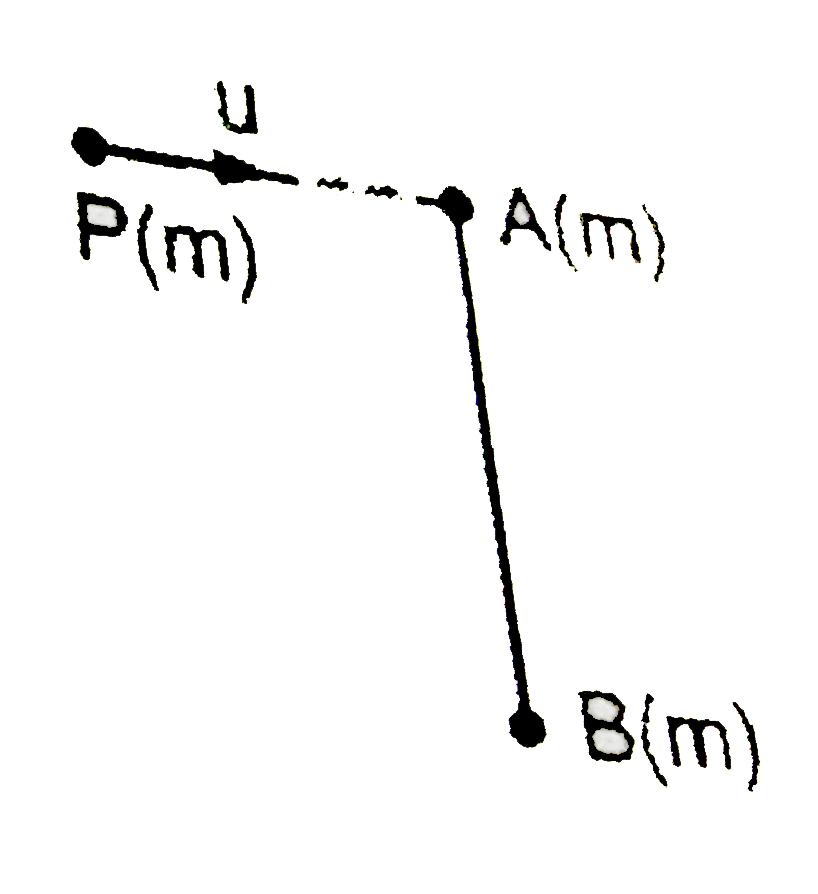
Two particle A and B, of mass m each, are joined by a rigid massless rod of length l. A particle P mass m, moving with a speed u normal to AB, strikes A and sticks to it. The centre of mass of the 'A+B+P' system is C.AThe velocity of C before impact is u/3.BThe velocity of C after impact is u/3CThe velocity of 'A+P' immediately after impact is u/2.DThe velocity of B immediately after impact is zero. - Question 3 - Select One
A particle of mass m moving with velocity v strikes a stationary particle of mass 2m and sticks to it. The speed of the system will be.
Av//2B2 vCv//3D3 v
A uniform rod of mass 2 kg and length 1 m lies on a smooth horizontal plane. A particle of mass 1 kg moving at a speed of 2m/s perependicular to the length of the rod strikes it at a distance 14 m from the centre and stops . Find the angular velocity of the rod about its centre just after the collision (in rad/s)
View SolutionA uniform rod of mass M and length L lies on a frictionless horizontal plane. A particle of same mass M moving with speed v0 perpendicular to the length of the rod strikes the end of the rod and sticks to it. Find the velocity of the center of mass and the angular velocity about the center of mass of (rod + particle) system.
View SolutionA particle of mass 2m moving with velocity v strikes a stationary particle of mass 3m and sticks to it . The speed of the system will be
View SolutionA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
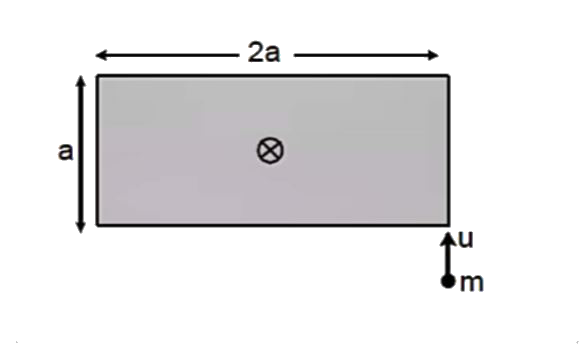
Find the angular momentum of the particle and of then about the centre of mass C before the collision.View SolutionA particle of mass m moving with speed u collides with the plate of mass m and sticks to it as shown in figure. The recangular place is free to rotae about an axis passing through the centre in horizontal plane. After the collision, the angular velocity of the place will be:
 View Solution
View Solution

