Two horizontal discs A and B of radii r and 2r having moments of inertia I and 4I about their axes. Initially, disc A is rotating with ω0 and disc B is at rest. Their rims are now brought in contact. The discs first slip over each other at the contact but slipping finally ceases due to the fricition between them. Find the angular speeds of the discs after the slipping ceases. Also, find the loss in kinetic energy.
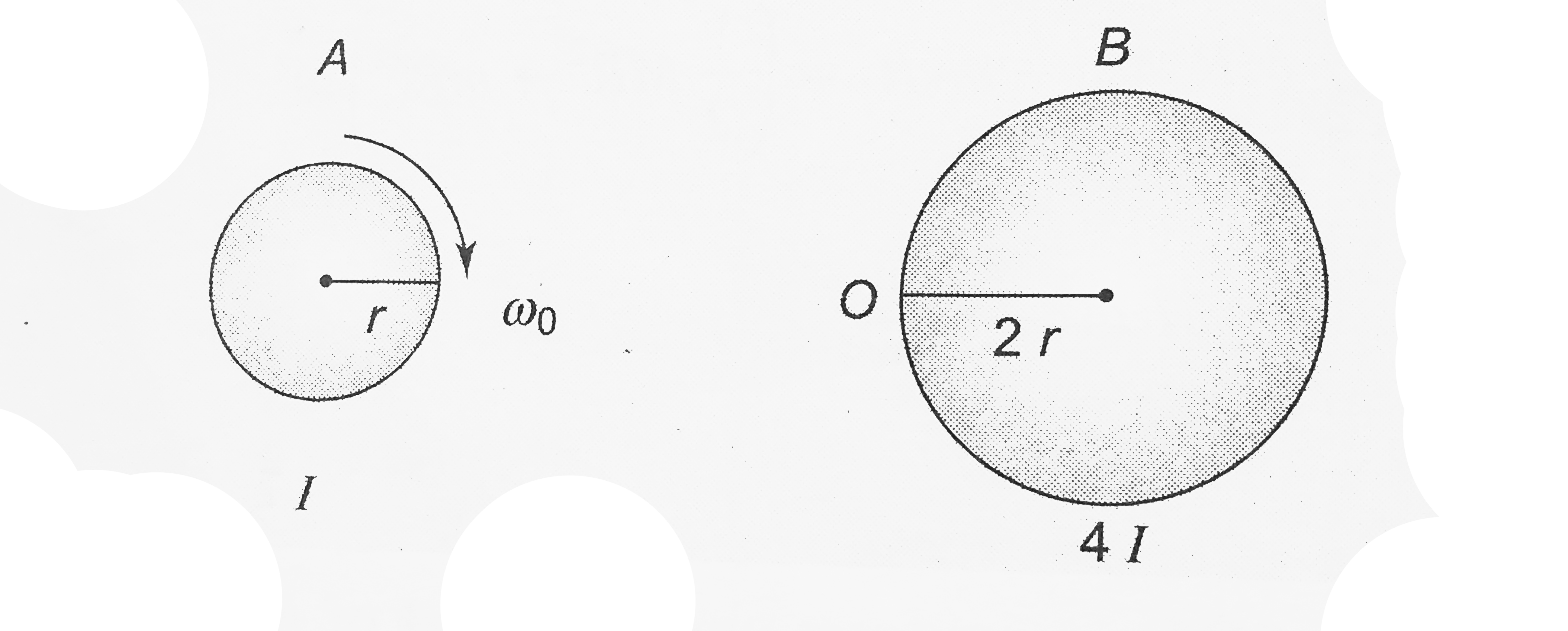
The friction between discs will disappear when there is no relative motion between them, i.e. their linear speed at the point of contact is same, i.e.
ω1r=ω2×2r (i)

The friction will decrease angular speed of A while it will increase angular speed of B. Let the friction act for time t.

Angular impulse
A:−t=I(ω1−ω0) (ii)
B:f×2rt=4I(ω2−0) (iii)
Dividing (ii) by (iii), we get
−12=ω1−ω04ω2=ω1−ω04ω12 (since ω2=ω12)
−ω1=ω1−ω0⇒ω1=ω02
ω2=ω12=ω04
Initial K.E.,Ki=12Iω20
Final K.E.,Kf=12I(ω02)2+12×4I(ω04)2
Iω208+Iω208=14Iω20
Loss in K.E.=Ki−Kf=14Iω20

Topper's Solved these Questions
Similar Questions
Figure shows two cylinders of raddi r1andr2 having moments of inertia I1andI2 about their respective axes. Initially the cylinders rotate about their axes with angular speed ω1andω2 as shown in the figure. The cylinders are moved closer to touch each other keeping the axes parallel. The cylinders first slipover each other at the contact but the slipping finally ceases due to the friction between them. Find the angular speeds of the sylinders after the slipping ceases.
 View Solution
View Solution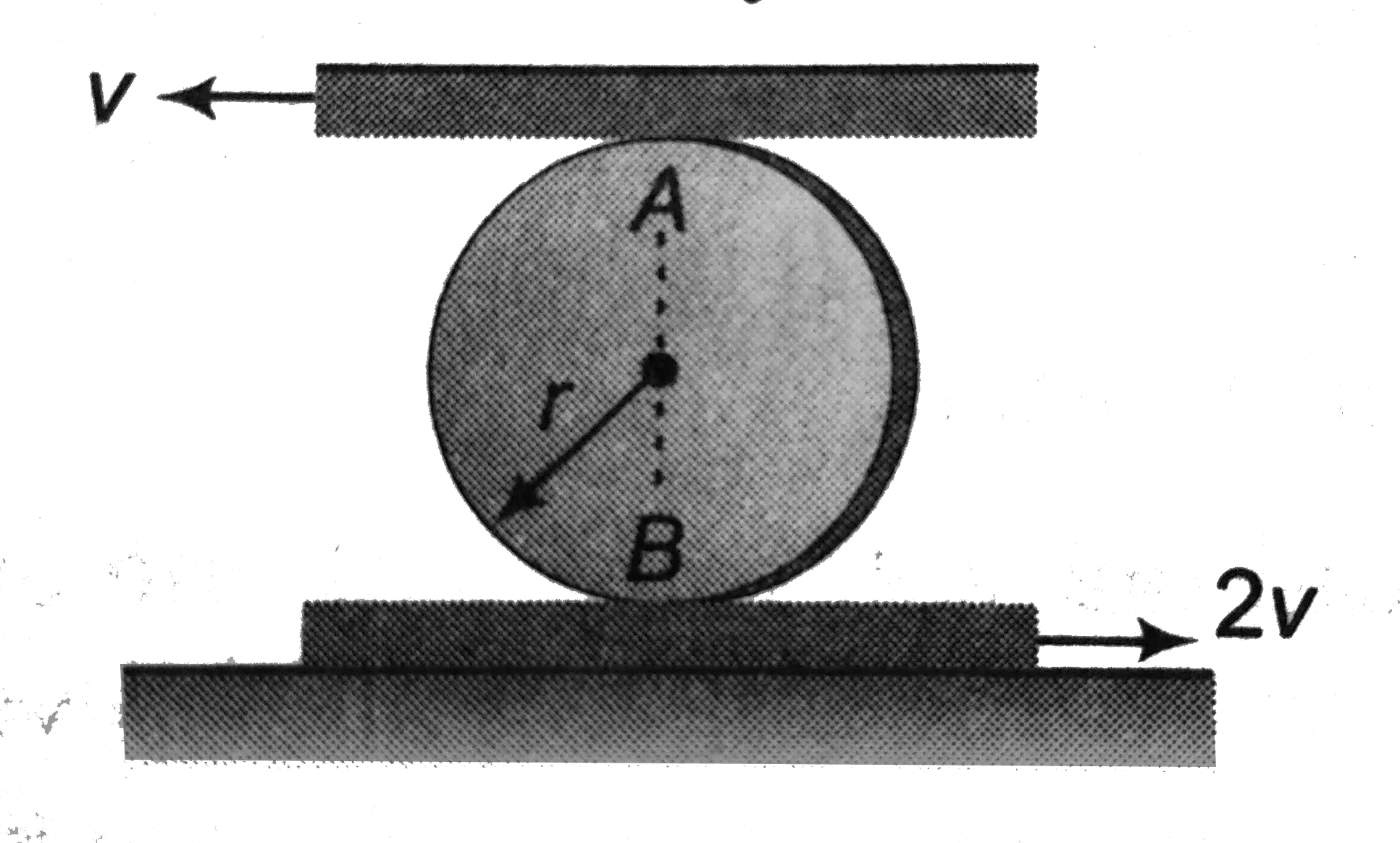
the disc of the radius r is confined to roll without slipping at A and B if the plates have the velocities shown, determine the angular velocity of the disc.View Solution
Knowledge Check
- Question 1 - Select One or More
Two horizontal discs of different radii are free to rotate about their central vertical axes: One is given some angular velocity, the other is stationary. Their rims arc now brought in contact. There is friction between the rims. Then
Athe force of friction between the rims will disappear when the discs rotate with equal angular speedsBthe force of friction between the rims will when they have equal linear velocitiesCthe angular momentum of the system will conservedDthe rotational kinetic energy of the system will not conserved - Question 2 - Select One
Two discs of moments of inertia I1 and I2 about their respective axes , rotating with angular frequencies ω1 and ω2 respectively, are brought into contact face to face with their axes of rotation coincident. The angular frequency of the composite disc will be
AI1ω1+I1ω2I1+I2BI2ω1+I1ω2I1+I2CI1ω1−I2ω2I1−I2DI2ω1−I1ω2I1−I2 - Question 3 - Select One
Two discs of moments of inertia I1 and I2 about their respective axes, rotating with angular frequencies, ω1 and ω2 respectively, are brought into contact face to face with their axes of rotation coincident. The angular frequency of the composite disc will be A.
AI1ω1+I2ω2I1+I2BI2ω1+I1ω2I1+I2CI1ω1+I2ω2I1−I2DI2ω1+I1ω2I1−I2
Two discs of moments of inertia I1andI2 about their respective axes (normal to the disc and passing through the centre) and rotating with angular speeds ω1andω2 are brought into contact face to face with their axes of rotation coincident.
(a) Does the law of conservation of angular momentum apply to the situation ? Why ?
(b) Find the angular speed of the two-disc system.
(c ) Calculate the loss in kinetic energy of the system in the process.
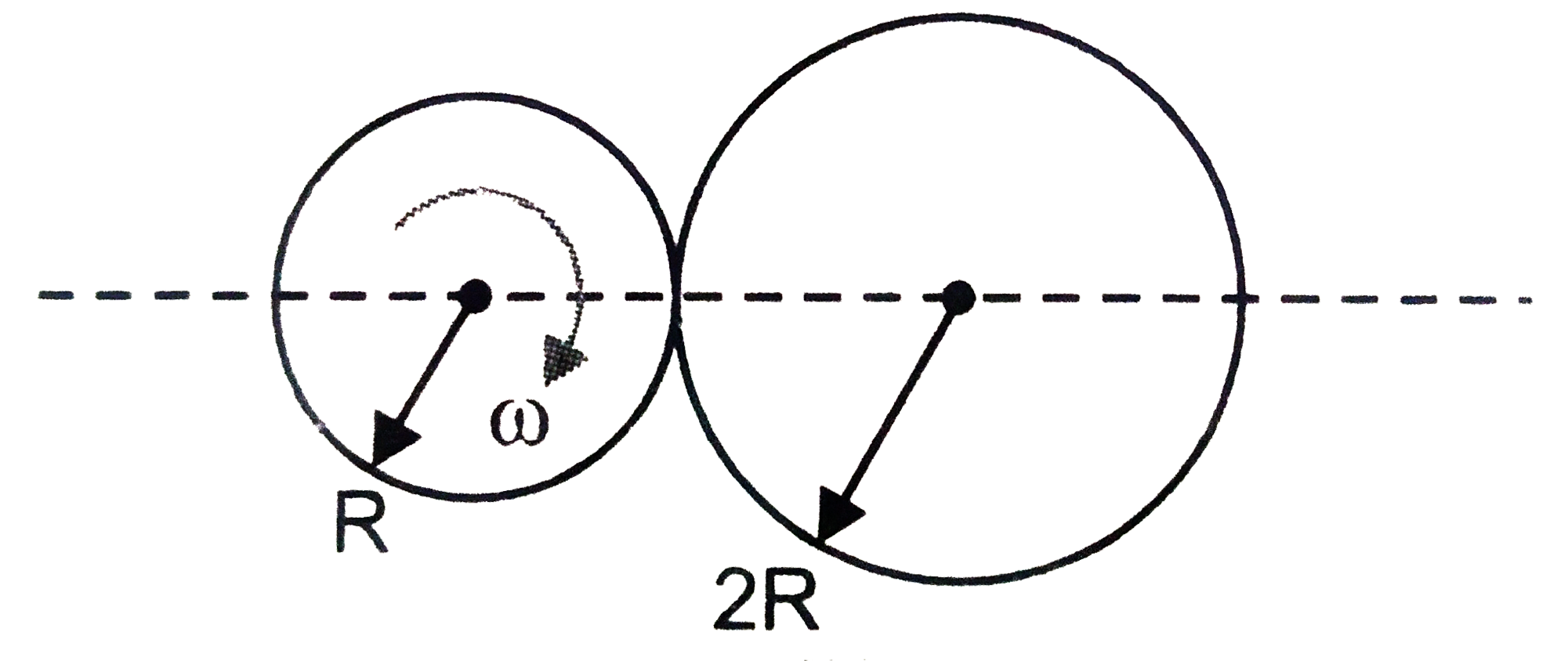
(d) Account for this loss.View SolutionTwo discs of radii Rand2R are pressed against eachother. Initially, disc wit radius R is rotating with angular velocity ω and other disc is stationary. Both discs are hinged at their respective centres and are free to rotate about them. Moment of inertiaof smaller disc is I and of bigger disc is 2I about their respective axis of rotation. Find the angular velocity of bigger disc after long time.
 View Solution
View SolutionTwo discs of moments of inertia I1andI2 about their respective axes (normal to the disc and passing through the centre), and rotating with angular speed ω1andω2 are brought into contact face to face with their axes of rotation coincident . What is the angular speed of the two-disc system ?
View SolutionTwo discs of moments of inertia I1andI2 about their respective axes (normal to the disc and passing through the centre), and rotating with angular speed ω1andω2 are brought into contact face to face with their axes of rotation coincident (i) What is the angular speed of the two-disc system ? (ii) Show that the kinetic energy of the combined system is less than the sum of the initial kinetic energies of the two discs. How do you account for this loss in energy ? Take ω1≠ω2.
View SolutionIf two circular discs A and B are of same mass but of radii r and 2r respectively, then the moment of inertia of A is
View Solution

