How are stationary waves formed in closed pipes ? Explain the various modes of vibrations and obtain relations for their frequencies.
Text Solution
A pipe, Which is closed at one end and the other is opened is called closed pipe. When a sound wave is sent through a closed pipe, which gets reflected at the closed end of the pipe.Then incident and reflected waves are in same frequency, travelling in the opposition direction are superimposed stationary waves are formed.
To form the stationary wave in closed pipe, which has atleast a node at closed end and antinode at open end of the pipe, it is known as first harmonic in closed pipe. Then length of the pipe ( l ) is equal to one fourth of the wave length.
∴l=λ14⇒λ1=4l
If 'v1' is fundamental frequency then
v1=υλ1 where 'υ'is velocity of sound in air
v1=υ4l=v ...(1)
To form the next harmonic in closed pipe, two nodes and two antinodes should be formed. So that there is possible to form third harmonic in closed pipe. Since one more node and antinode should be included.
Then length of the pipe is equal to 34 of the wavelength
∴l=3λ34 where 'λ3' is wavelength of third harmonic
λ3=4l3
If 'v3' is third harmonic frequency ( first overtone )
∴v3=υλ3=3υ4l
v3=3v ...(2)
Similarly the next overtone in the close pipe is only fifth harmonic it will have three nodes and 3 antinodes between the closed end and open end.
Then length of the pipe is equal to 54 of wave length (λ5)
∴l=5λ54 where 'λ5' is wave length of fifth harmonic .
λd5=4l5
If 'v5' is frequency of fifth harmonic ( second overtone )
v5=υλ5=5υ4l
v5=5v ...(3)
∴ The frequencies of higher harmonics can be determined by using the same procedure . Therefore from the Eq (1) , (2) and(3)only odd harmonics are formed.
Therefore the ratio of the frequencies of harmonics in closed pipe can be written as
v1:v3:v5=v:3v:5v
v1:v3:v5=1:3:5

|
Topper's Solved these Questions
- WAVESBOOK - VIKRAM PUBLICATION ( ANDHRA PUBLICATION)CHAPTER - WAVESEXERCISE - TEXTUAL EXERCISES
21 Videos
- WAVESBOOK - VIKRAM PUBLICATION ( ANDHRA PUBLICATION)CHAPTER - WAVESEXERCISE - ADDITIONAL EXERCISES
6 Videos
- WAVESBOOK - VIKRAM PUBLICATION ( ANDHRA PUBLICATION)CHAPTER - WAVESEXERCISE - SHORT ANSWER QUESTIONS
11 Videos
- WAVE OPTICS BOOK - VIKRAM PUBLICATION ( ANDHRA PUBLICATION)CHAPTER - WAVE OPTICS EXERCISE - Problems
6 Videos
Similar Questions
Knowledge Check
Stationary waves in closed pipe will produce
Aall the harmonics.Ball the even harmonics.Call the odd harmonics.Dno harmonics.when a stationary wave is formed then its frequency is
Asame as that of the individual wavesBtwice that of the individual wavesChalf that of the individual wavesD√2 that of the individual waveswhen a stationary wave is formed then its frequency is
Asame as that of the individual wavesBtwice that of the individual wavesChalf that of the individual wavesD√2 that of the individual waves
The frequencies of stationary waves formed in closedend organ pipes are in the ratio 1:3:5:7…..
View SolutionWhen a stationary wave is formed then its frequency is
View SolutionWhen a stationary wave is formed, then its frequency is
View SolutionModes of vibration in an open organ pipe are represented by –
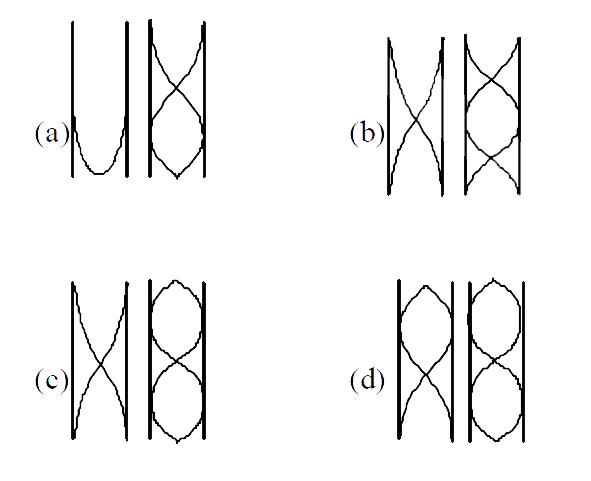
View SolutionAmplitude of vibration in stationary wave is
View Solution
