A unit positive point charge of mass m is projected with a velocity V inside the tunnel as shown. The tunnel has been made inside a uniformly charged nonconducting sphere. The minimum velocity with which the point charge should be projected such that it can reach the opposite end of the tunnel is equal to

[ρR2/4mε0]1/2
[ρR2/24mε0]1/2
[ρR2/6mε0]1/2
zero because the initial and the fianl points are at same potential.
The correct Answer is:a
If we throw the charged particle just right of the center of the tunnel, the particle will cross the tunnel. Hence, applying conservation of momentum between start point and center of tunnel we get
ΔK+ΔU=0
or (0+12mv2)+q(Vf−Vi)=0
or Vf=Vs2(3−r2R2)=ρR26ε0(3−r2R2)
Hence r=R2
Vf=ρR26ε0(3−R24R2)=11ρR224ε0,Vi=ρR23ε0
12mv2=1[11ρ2R224ε0−ρR23ε0]=ρR2ε0[1124−13]=ρR28ε0
or V=(ρR24mε0)1/2
Hence velocity should be slightly greater than V.
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - Multiple Correct
10 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - Comprehension
31 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - Subjective
28 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
The minimum velocity v with which charge q should be projected so that it manages to reach the centre of the ring starting from the position shown in figure is
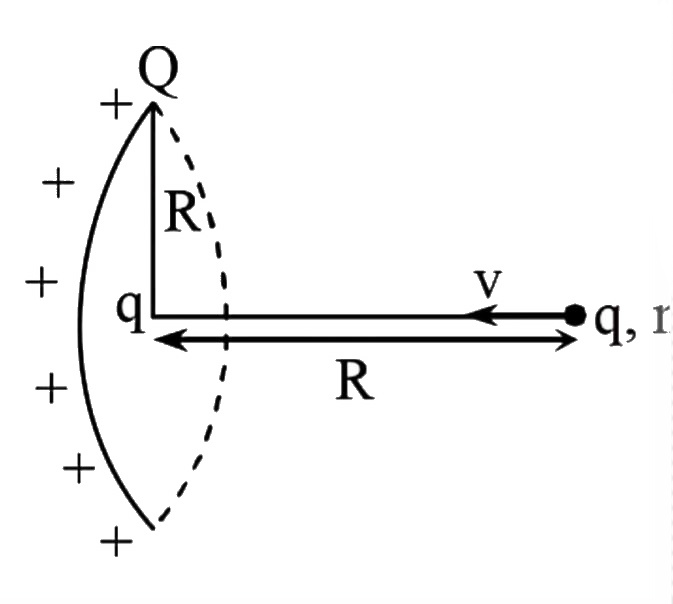
View SolutionA particle of charge q is projected from point P with velocity v as shown. Choose the correct statement from the following.

View Solution
Knowledge Check
A unit positive point charge of mass m is projected with a velocity v inside the tunnel as shown. The tunnel has been made inside a uniformly charged nonconducting sphere. The minimum velocity with which the point charge should be projected such it can it reach the opposite end of the tunnel is equal to
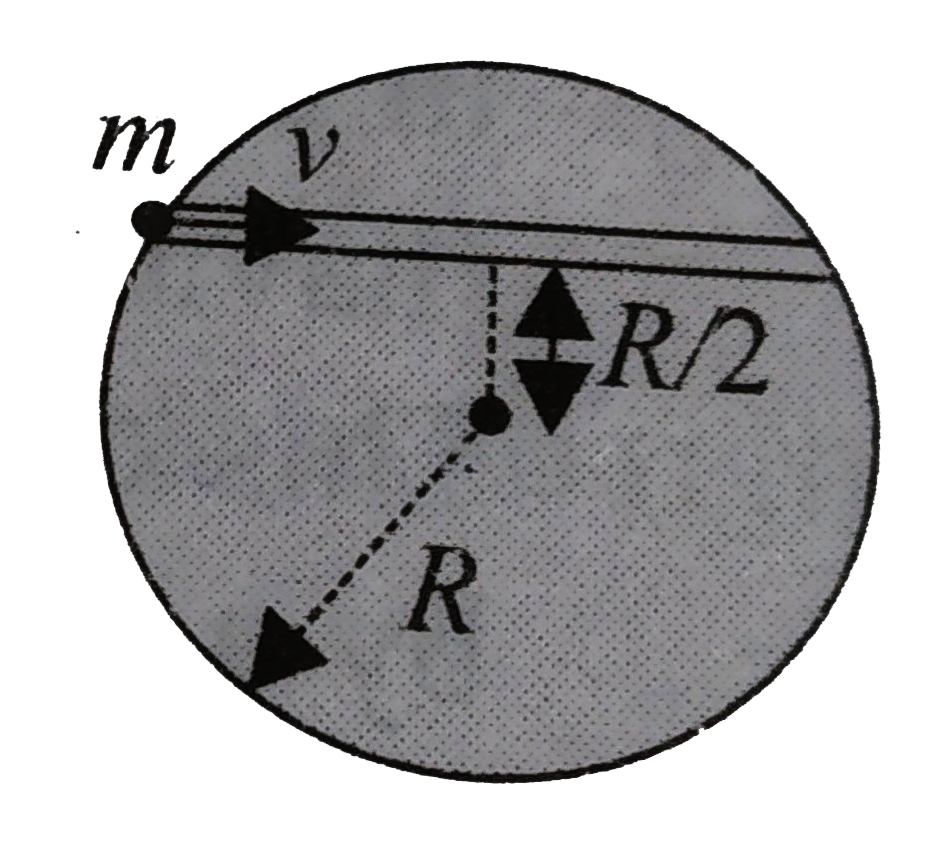 A[ρR2/4mε0]12B[ρR2/24mε0]12C[ρR2/6mε0]12Dzero because the initial and the final points are at same potential
A[ρR2/4mε0]12B[ρR2/24mε0]12C[ρR2/6mε0]12Dzero because the initial and the final points are at same potentialA unit positive point charge of mass m is projected with a velocity v inside the tummel as shown. The tunnel has been made inside a uniformly charged non conducting sphere. The minimum velocity with which the point charge should be projected such that it can it reach the opposite end of the tunnel, is equal to:
 A[ρR24mε0]1/2B[ρR224mε0]1/2C[ρR26mε0]1/2Dzero because the initial and the final points are at same potential
A[ρR24mε0]1/2B[ρR224mε0]1/2C[ρR26mε0]1/2Dzero because the initial and the final points are at same potentialThe minimum velocity v with which charge q should be projected so that it manages to reach the centre of the ring starting from the position shown in figure is
 Av=√kQqmR(2−√2)Bv=√kQq2mR(2−√2)Cv=√kQqmRDv=√kQq√2mR(1−√2)
Av=√kQqmR(2−√2)Bv=√kQq2mR(2−√2)Cv=√kQqmRDv=√kQq√2mR(1−√2)
A charge +Q is uniformly distributed in a spherical volume of radius R. A particle of charge +q and mass m projected with velocity v0 the surface of the sherical volume to its centre inside a smooth tunnel dug across the sphere. The minimum value of v0 such tht it just reaches the centre (assume that thee is no resistance on the particle except electrostatic force) of he sphericle volume is
View SolutionA point charge of charge -q and mass m is released with negligible speed from a distance √3R on the axis of a fixed uniformly charged ring of charge Q and radius R. Find out its velocity when it reaches it reaches at the centre of the ring.

View SolutionThe adjoining figure represent a semi-circular loop of charge Q and of radius R .The minimum velocity with which a point mass mof charge −q should be projected so that it becoems free from the influence of the loop is

View SolutionA particle of charge q is projected from point P with velocity v as shown. Choose the correct statement from the following.

View SolutionA charge +Q is uniformly distributed in a spherical volume of radius R. A particle of charge +q and mass m projected with velocity v0 the surface of the sherical volume to its centre inside a smooth tunnel dug across the sphere. The minimum value of v0 such tht it just reaches the centre (assume that thee is no resistance on the particle except electrostatic force) of he sphericle volume is
View Solution
