Question

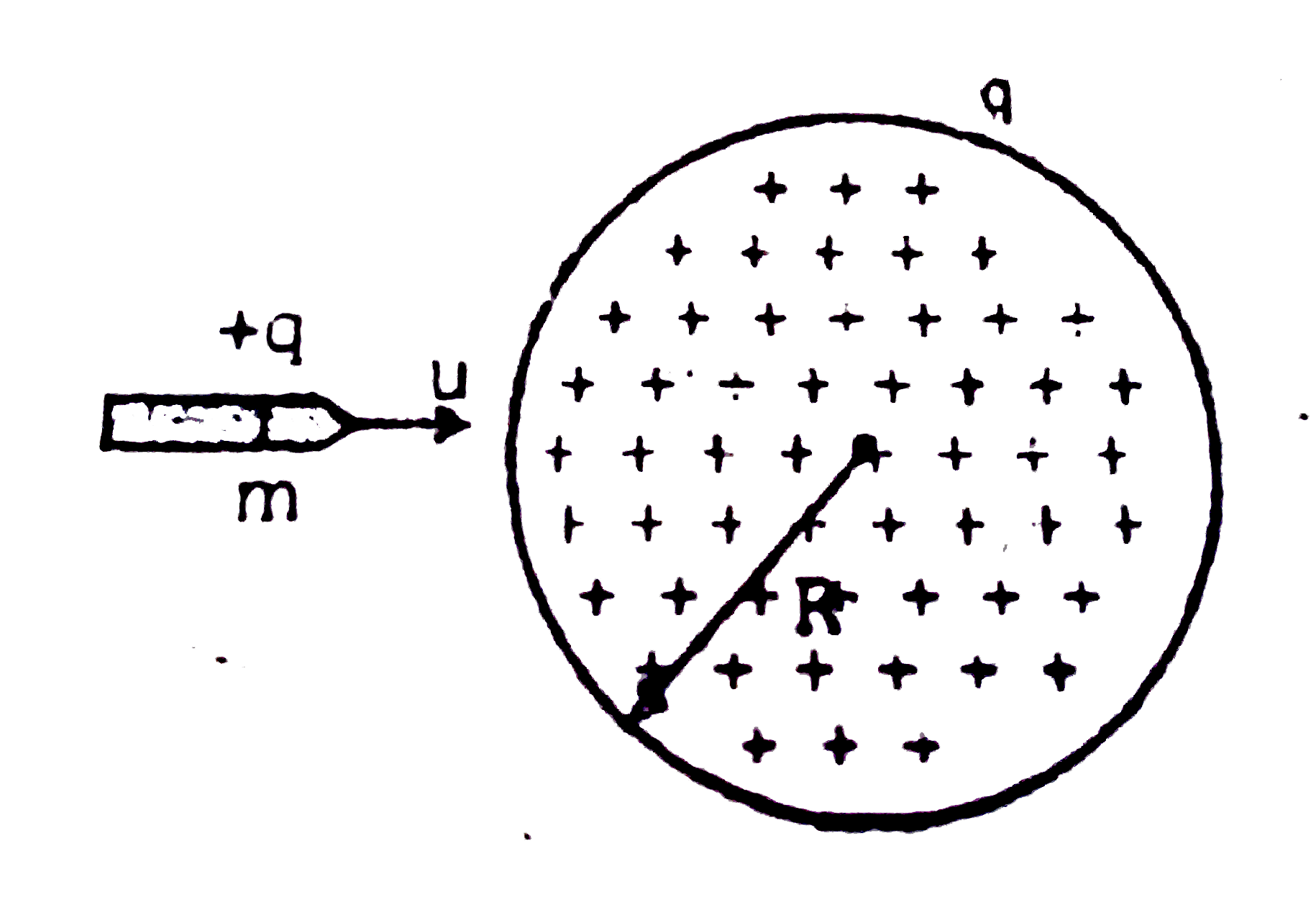
A charge $+Q$ is uniformly distributed in a spherical volume of radius R. A particle of charge $+q$ and mass m projected with velocity $v_0$ the surface of the sherical volume to its centre inside a smooth tunnel dug across the sphere. The minimum value of $v_0$ such tht it just reaches the centre (assume that thee is no resistance on the particle except electrostatic force) of he sphericle volume is

Options

A. `sqrt((Qq)/(2piepsilon_0mR))`
B. `sqrt((Qq)/(piepsilon_0mR))`
C. `sqrt((2Qq)/(piepsilon_0mR))`
D. `sqrt((Qq)/(4piepsilon_0mR))`

Answer

D

Explanation

To solve the problem of finding the minimum velocity $$v_0$$ required for a particle of charge $$+q$$ and mass $$m$$ to reach the center of a spherical volume with a uniformly distributed charge $$+Q$$, we can use the principle of conservation of mechanical energy. Here’s a step-by-step solution:

Step 1: Understand the Initial and Final States
- The particle is projected from the surface of the sphere with velocity \( v_0 \).
- The initial kinetic energy (KE) of the particle is given by:
\( KE_{\text{initial}} = \frac{1}{2} mv_0^2 \)
- The initial potential energy (PE) when the particle is at the surface of the sphere is given by:
\( PE_{\text{initial}} = \frac{kQq}{R} \)
where \( k = \frac{1}{4\pi \epsilon_0} \).

Step 2: Determine the Final State
- At the center of the sphere, we want to find the potential energy (PE) and kinetic energy (KE).
- The potential energy at the center of the sphere is given by:
\( PE_{\text{final}} = kQq \cdot \left( \frac{3}{R} \right) = \frac{3kQq}{R} \)
- If the particle just reaches the center, we can assume that its final kinetic energy is zero (for minimum \( v_0 \)):
\( KE_{\text{final}} = 0 \)

Step 3: Apply Conservation of Mechanical Energy
Using the conservation of mechanical energy, we can equate the total initial energy to the total final energy:
\( KE_{\text{initial}} + PE_{\text{initial}} = KE_{\text{final}} + PE_{\text{final}} \)
Substituting the expressions we have:
\( \frac{1}{2} mv_0^2 + \frac{kQq}{R} = 0 + \frac{3kQq}{R} \)

Step 4: Rearranging the Equation
Rearranging the equation gives:
\( \frac{1}{2} mv_0^2 = \frac{3kQq}{R} - \frac{kQq}{R} \)
\( \frac{1}{2} mv_0^2 = \frac{2kQq}{R} \)

Step 5: Solve for \( v_0 \)
Now, we can solve for \( v_0^2 \):
\( mv_0^2 = \frac{4kQq}{R} \)
\( v_0^2 = \frac{4kQq}{mR} \)
Taking the square root gives:
\( v_0 = \sqrt{\frac{4kQq}{mR}} \)

Step 6: Substitute \( k \)
Substituting \( k = \frac{1}{4\pi \epsilon_0} \):
\( v_0 = \sqrt{\frac{4 \cdot \frac{1}{4\pi \epsilon_0} \cdot Qq}{mR}} = \sqrt{\frac{Qq}{\pi \epsilon_0 mR}} \)

Final Answer
Thus, the minimum value of \( v_0 \) required for the particle to just reach the center of the spherical volume is:
\( v_0 = \sqrt{\frac{Qq}{\pi \epsilon_0 mR}} \)