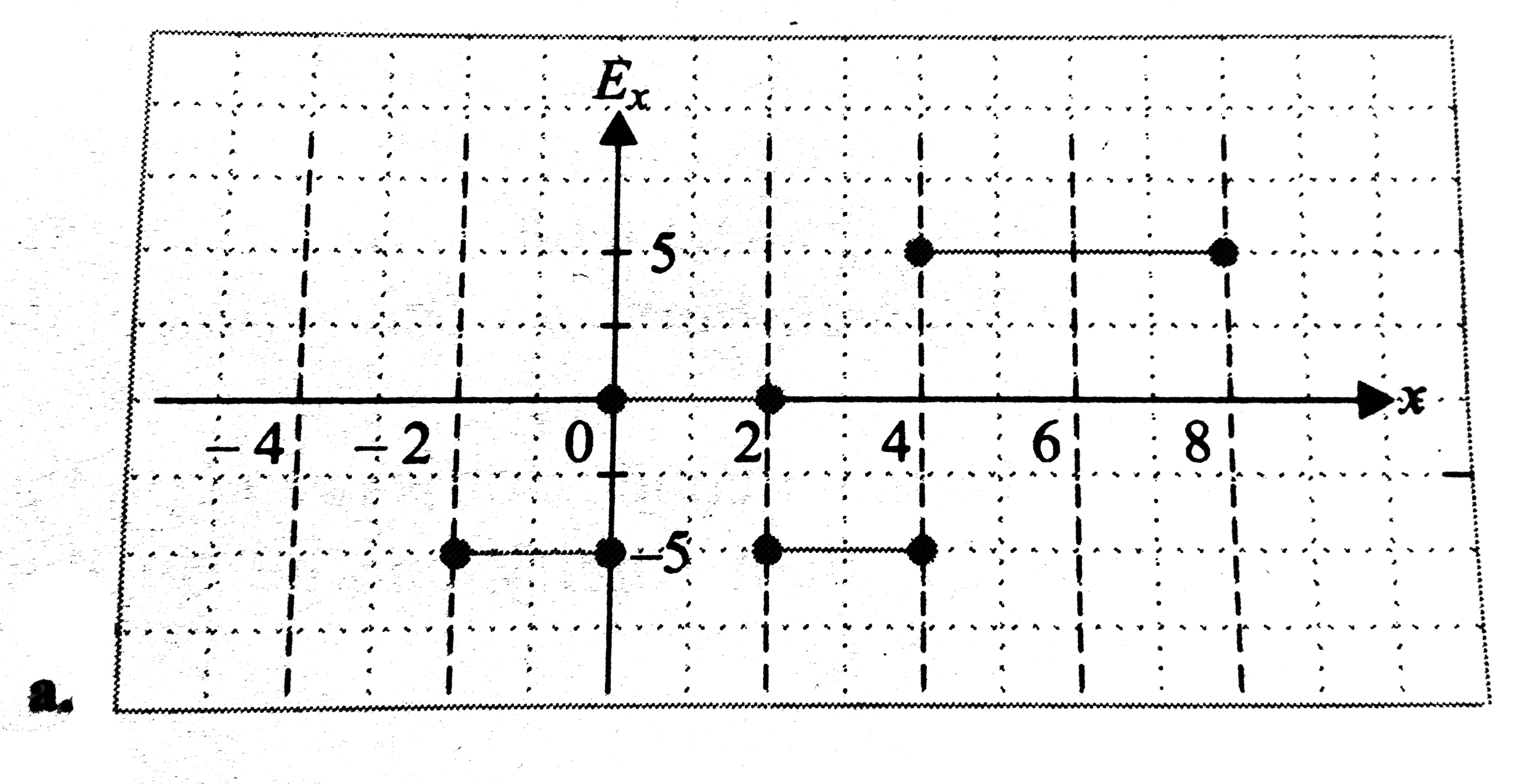
The electrical potential function for an electrical field directed parallel to the x-axis is shown in the given graph.
Draw the graph of electric field strength.

A

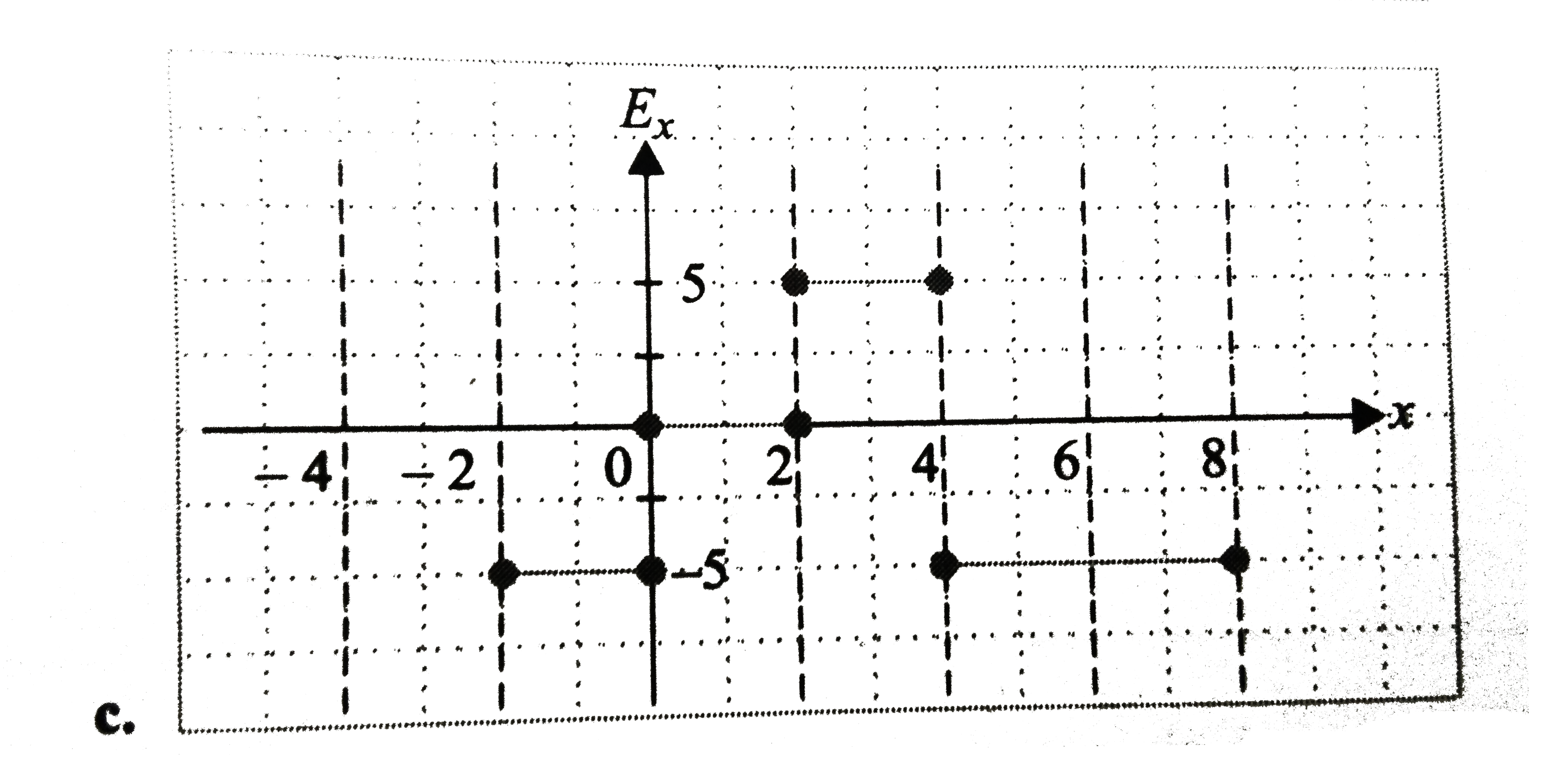
ocr_image

B

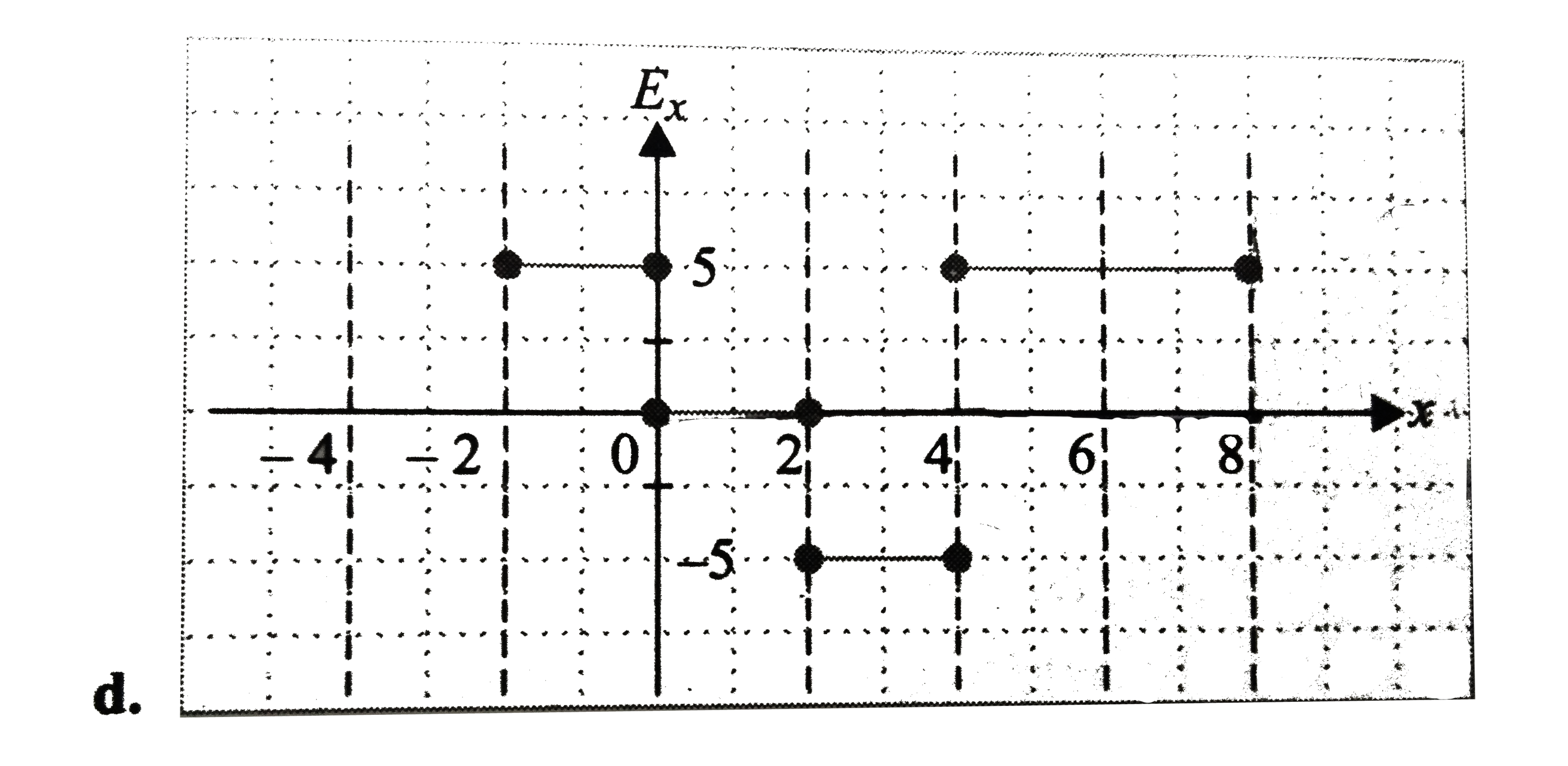
ocr_image

C

ocr_image

D

ocr_image

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

$E_{r} = - \frac{Δ V}{Δ r}, E_{x} = - \frac{Δ V}{Δ x}$
For $- 2 \leq x \leq 0, E_{x} = - \frac{(10 - 0)}{[0 - (- 2)]} = - 5 N C^{- 1}$
For $0 \leq x \leq 2, E_{x} = 0$
For $2 \leq x \leq 4, E_{x} = - \frac{[20 - 10]}{[4 - 2]} = - 5 N C^{- 1}$
For $4 \leq x \leq 8, E_{x} = - \frac{[0 - 20]}{[8 - 4]} = 5 N C^{- 1}$

Updated on:21/07/2023

|

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

The electrical potential function for an electrical field directed parallel to the x - axis is shown in (Fig. 3.152).
.
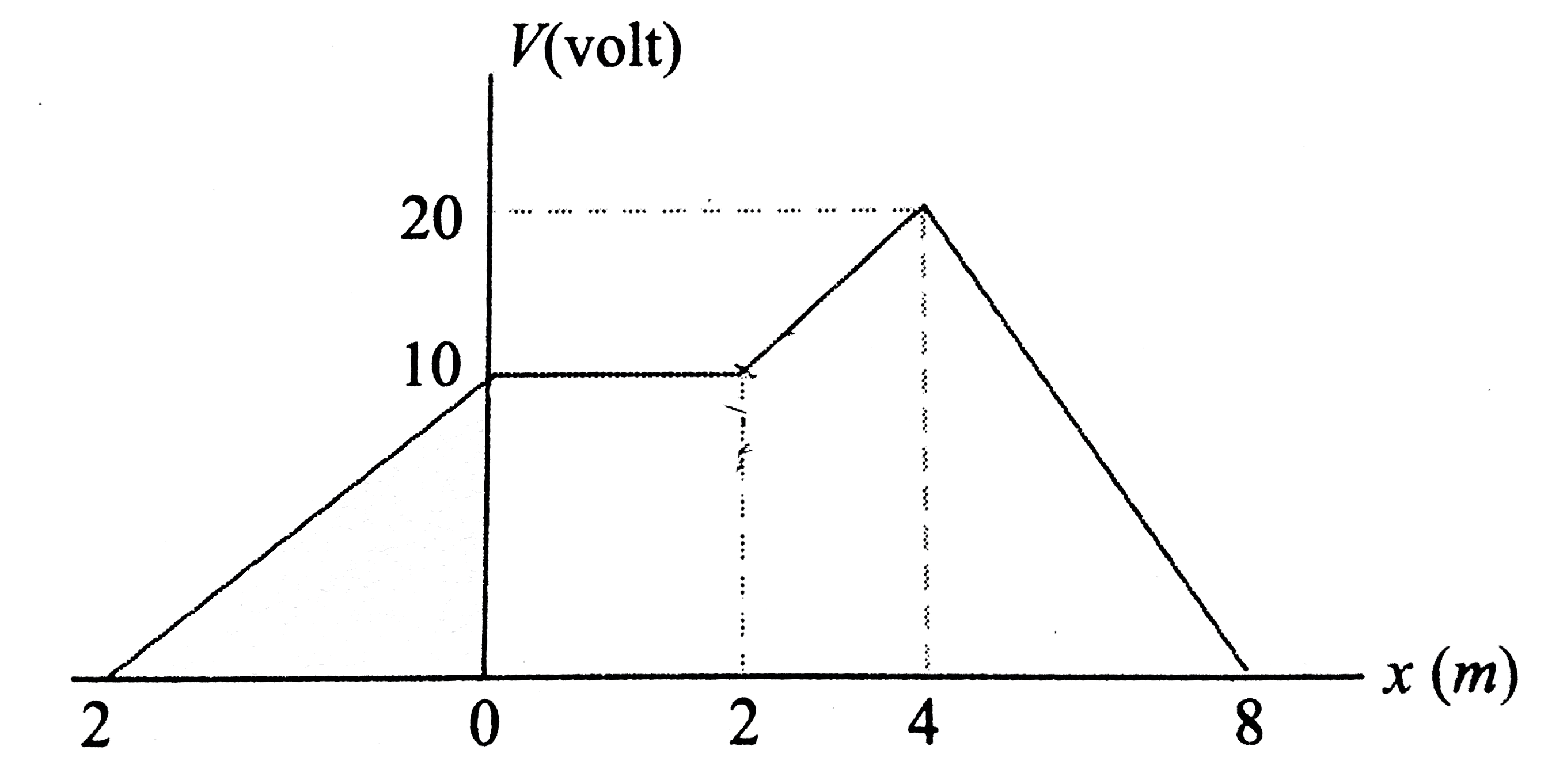The magnitude of the electric field in the x - direction in the interval $4 \leq x \leq 8$ is
A $2.5 N C^{- 1}$
B $5 N C^{- 1}$
C $- 2.5 N C^{- 1}$
D $- 5 N C^{- 1}$
In the following graph , the magnitude of maximum electric field is

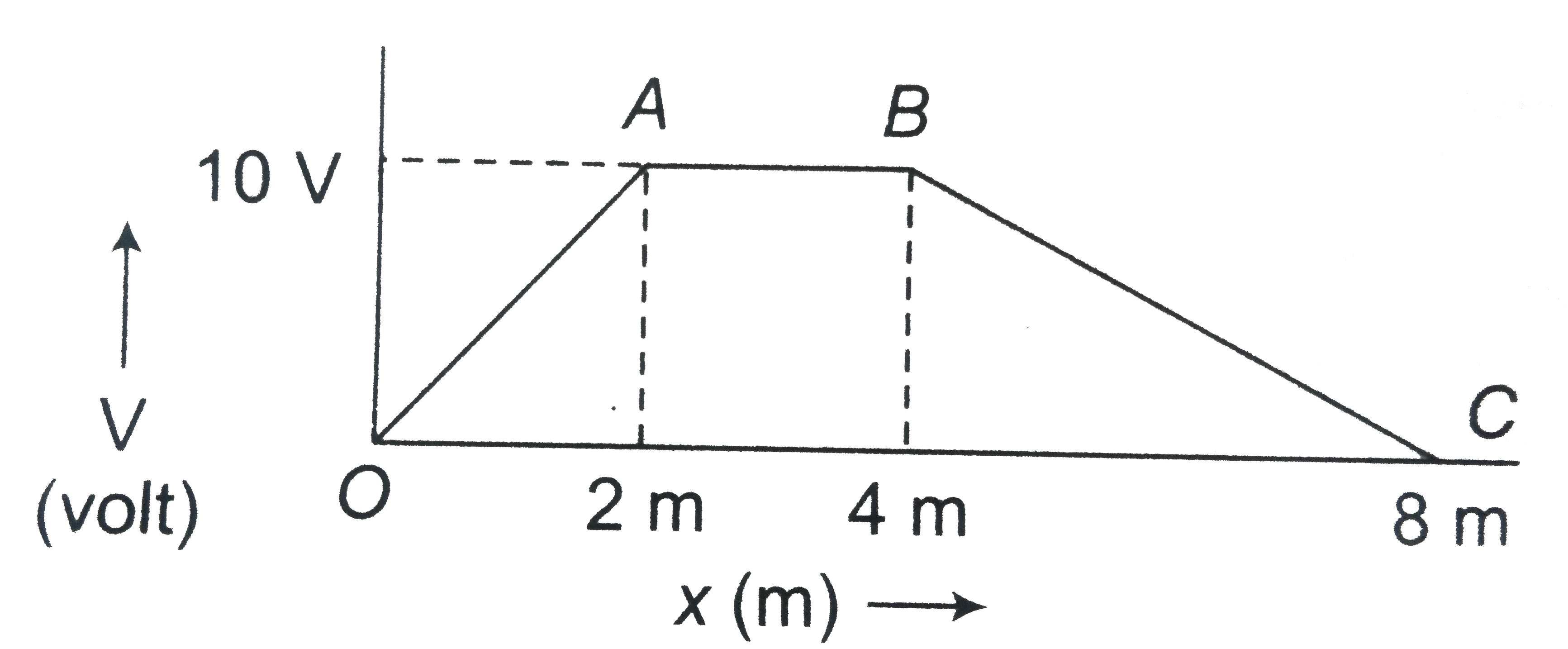A $5 V / m$
B $2.5 V / m$
C $1.25 V / m$
D $10 V / m$
Due to an electric dipole shown in fig., the electric field intensity is parallel to dipole axis :

Aat P only
Bat Q only
Cboth at P and at Q
Dneither at P nor at Q

CENGAGE PHYSICS-ELECTRIC POTENTIAL-Comprehension

Home
Ask Doubt
Profile