An uniform electric field of strength E exists in a region. An electron of mass m enters a point A perpendicular to x - axis with velocity V. It moves through the electric field and exists at point B. The components of velocity at B are shown in (Fig. 3.156). At B the y - component of velocity remain uncharged.
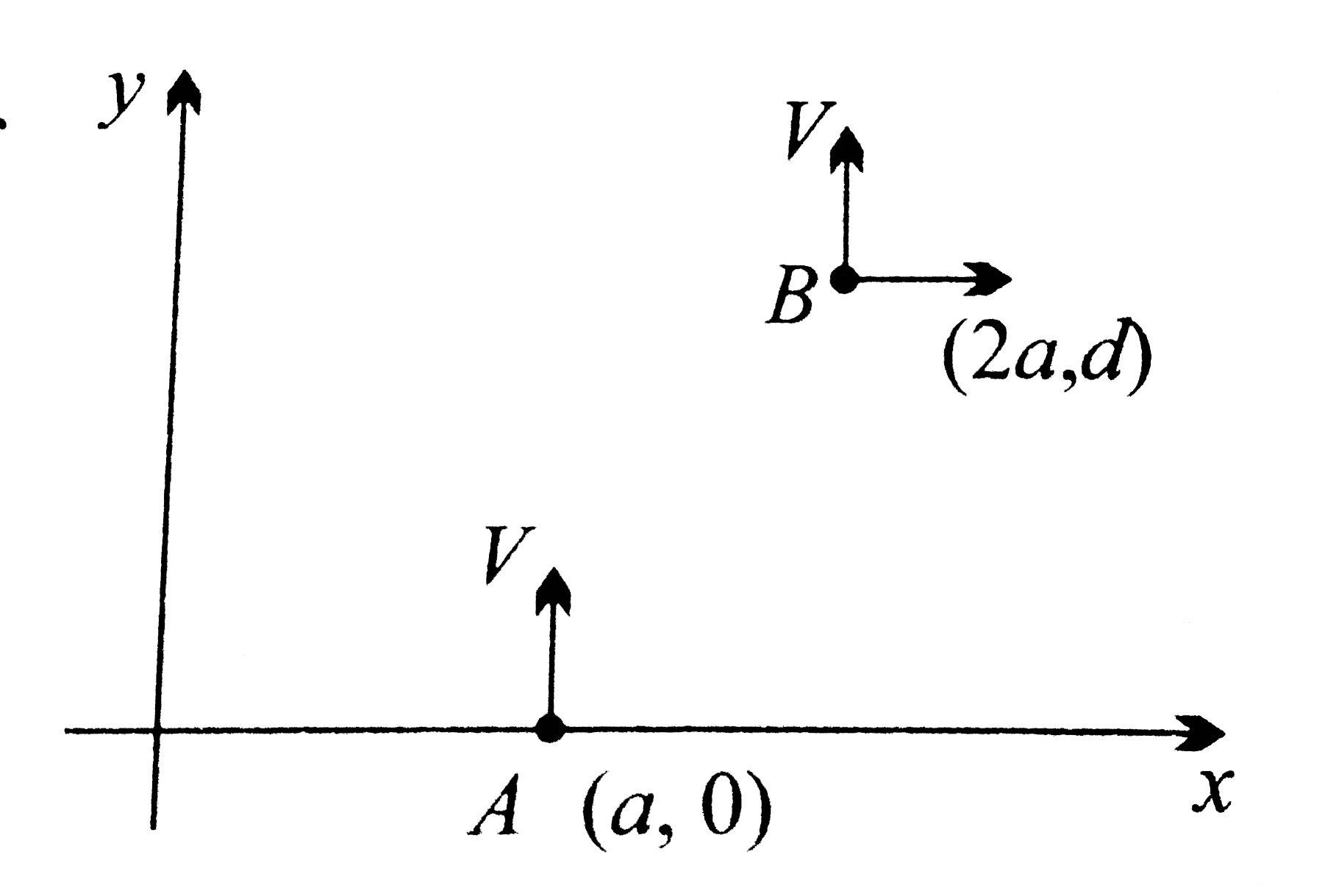 .
.
Find electric field.
2maV2ed2
maV2ed2
maV22ed2
2maV3ed3
The correct Answer is:A
Electric field should be an negative x - direction because velocity along y - direction remains constant.
Accleration of electron along x - axis is ax=eE/m.
Time taken to go from A to B is t=d/V.
Along x - axis
a=12(ax)t2=12eEm(dV)2
or E=2maV2ed2
v1=axt=eEmdV=emdV2maV2ed2=2adV
Velocity at Bis√V2+v21=V√1+(2ad)2
Rate of work done by field at B is
Fv1=eE2adV=2aeVd2maV2ed2=4ma2V3d3.
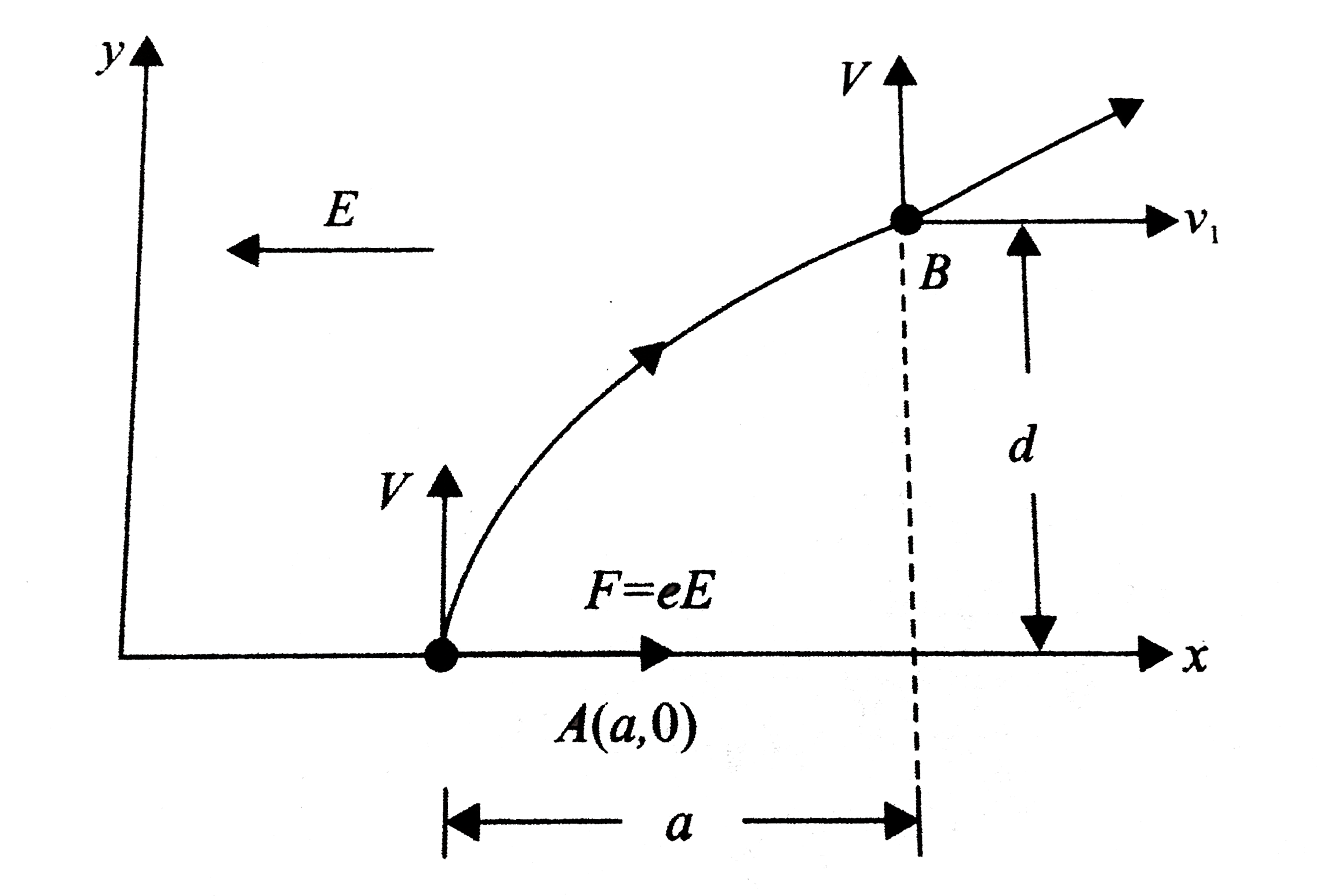 .
.
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - Integer
5 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.1
14 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - Multiple Correct
10 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
An uniform electric field of strength E exists in a region. An electron of mass m enters a point A perpendicular to x - axis with velocity V. It moves through the electric field and exists at point B. The components of velocity at B are shown in (Fig. 3.156). At B the y - component of velocity remain uncharged.
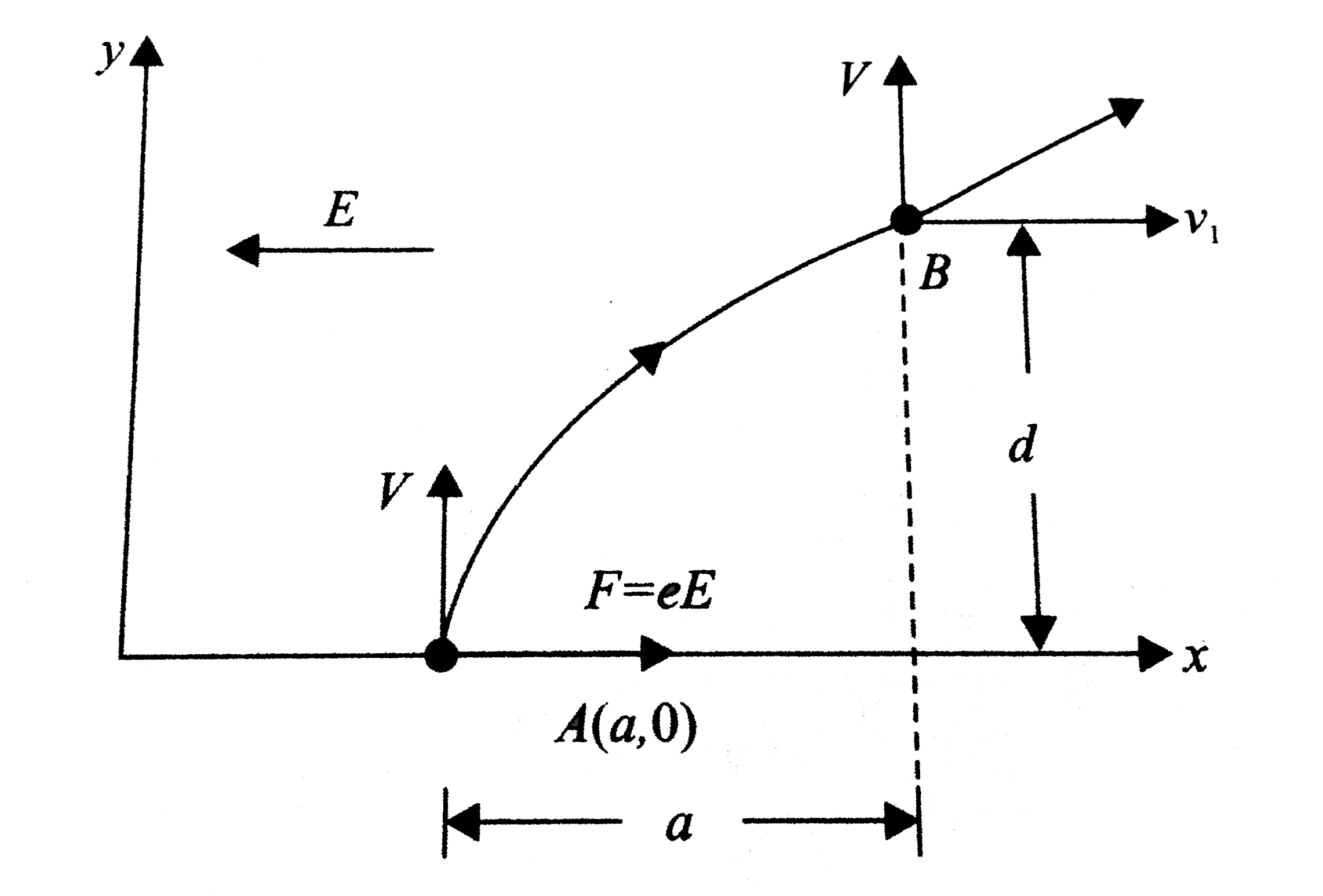 .
.
Find velocity at B.
View SolutionAn uniform electric field of strength E exists in a region. An electron of mass m enters a point A perpendicular to x - axis with velocity V. It moves through the electric field and exists at point B. The components of velocity at B are shown in (Fig. 3.156). At B the y - component of velocity remain uncharged.
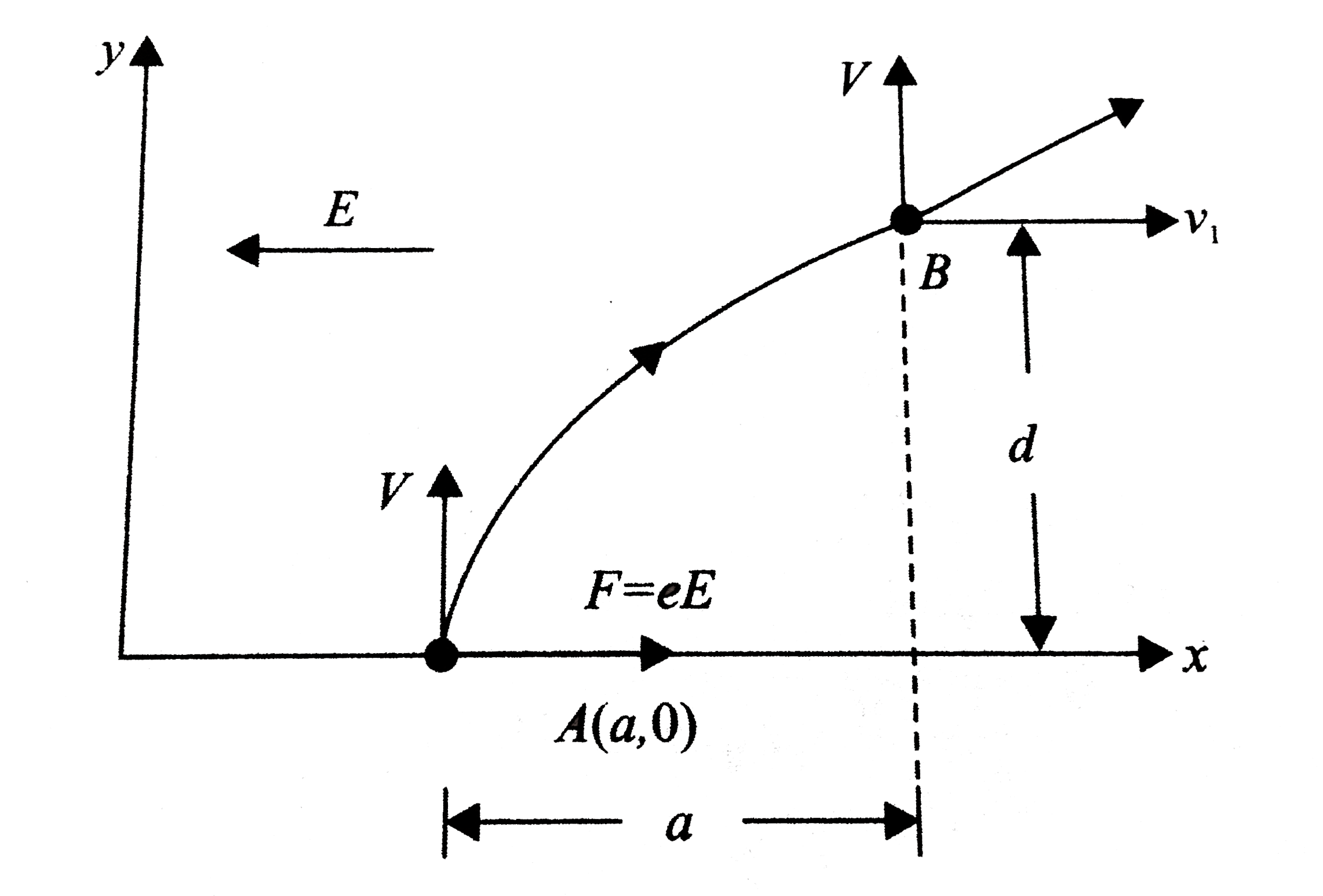
Find the rate of work done by the field at B.
View Solution
Knowledge Check
An uniform electric field of strength E exists in a region. An electron of mass m enters a point A perpendicular to x - axis with velocity V. It moves through the electric field and exists at point B. The components of velocity at B are shown in (Fig. 3.156). At B the y - component of velocity remain uncharged.
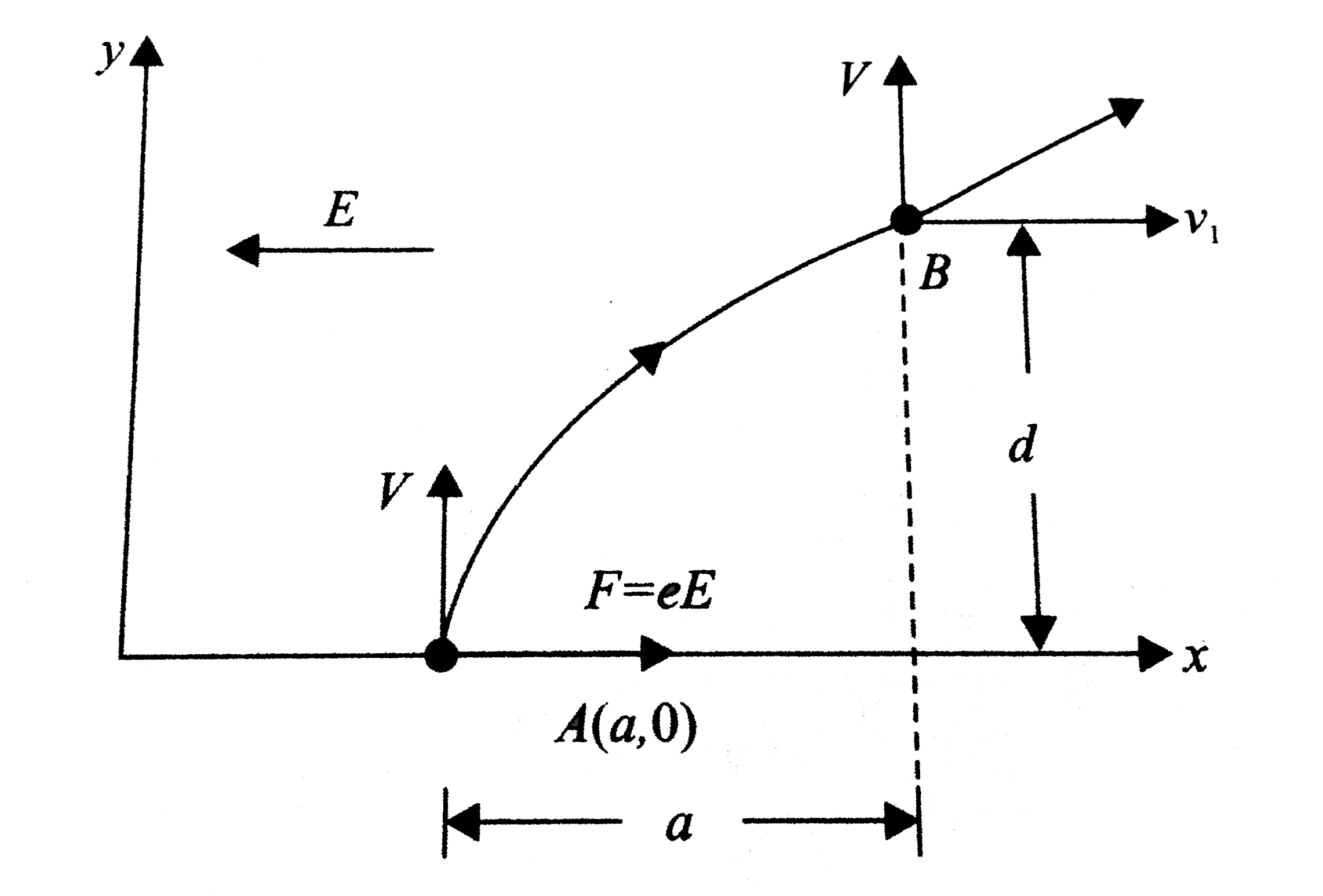 .
.
Find velocity at B.AV√1−(2ad)2BV√1+(2ad)2CV√1+(ad)2DV√2+(2ad)2An uniform electric field of strength E exists in a region. An electron of mass m enters a point A perpendicular to x - axis with velocity V. It moves through the electric field and exists at point B. The components of velocity at B are shown in (Fig. 3.156). At B the y - component of velocity remain uncharged.
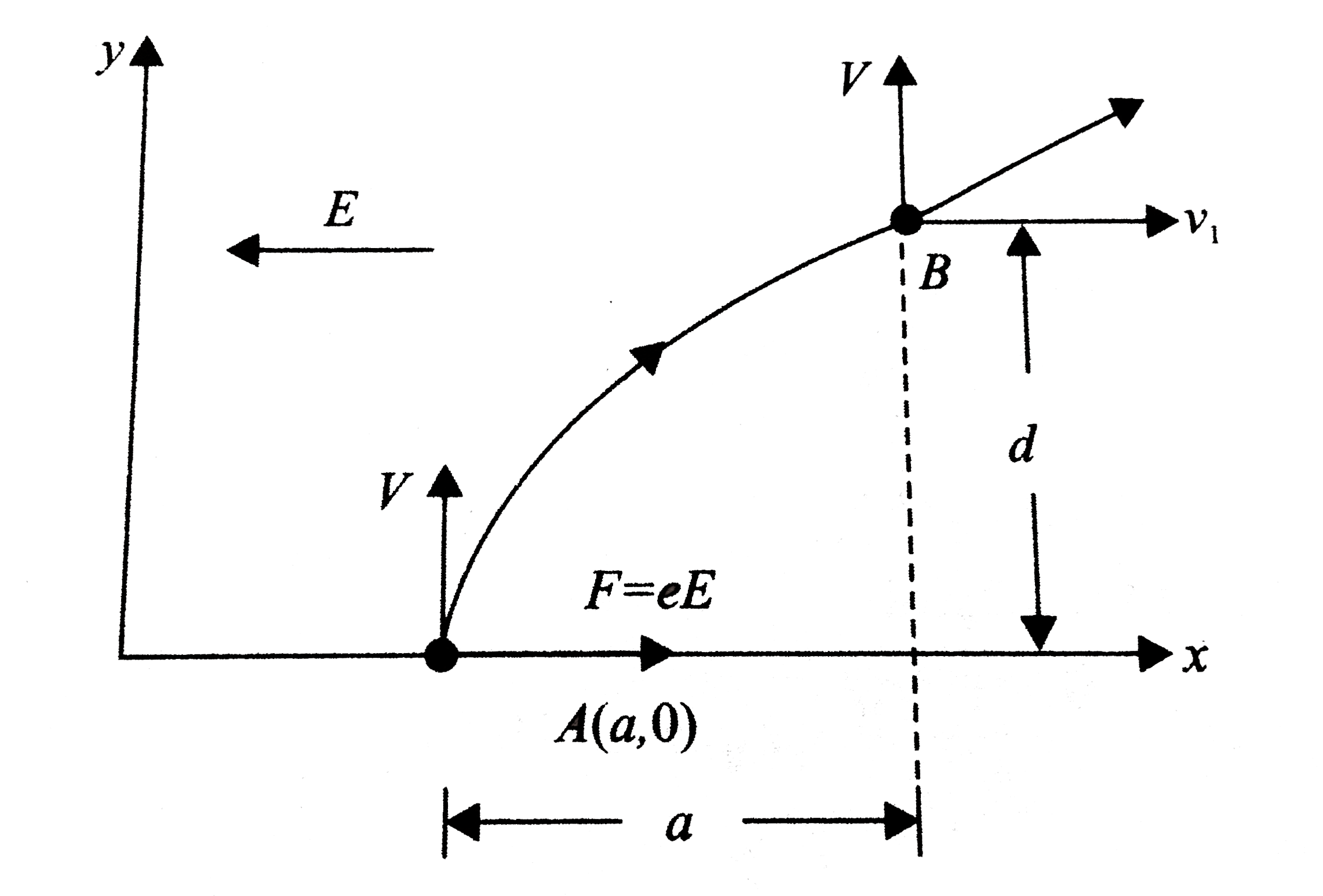
Find the rate of work done by the field at B.A2ma2V3d3Bma2V32d3C4ma2V3d3Dma2V3d3A uniform electric field of strength e exists in a region. An electron (charge -e, mass m) enters a point A with velocity Vˆj. It moves through the electric field & exits at point B. Then :
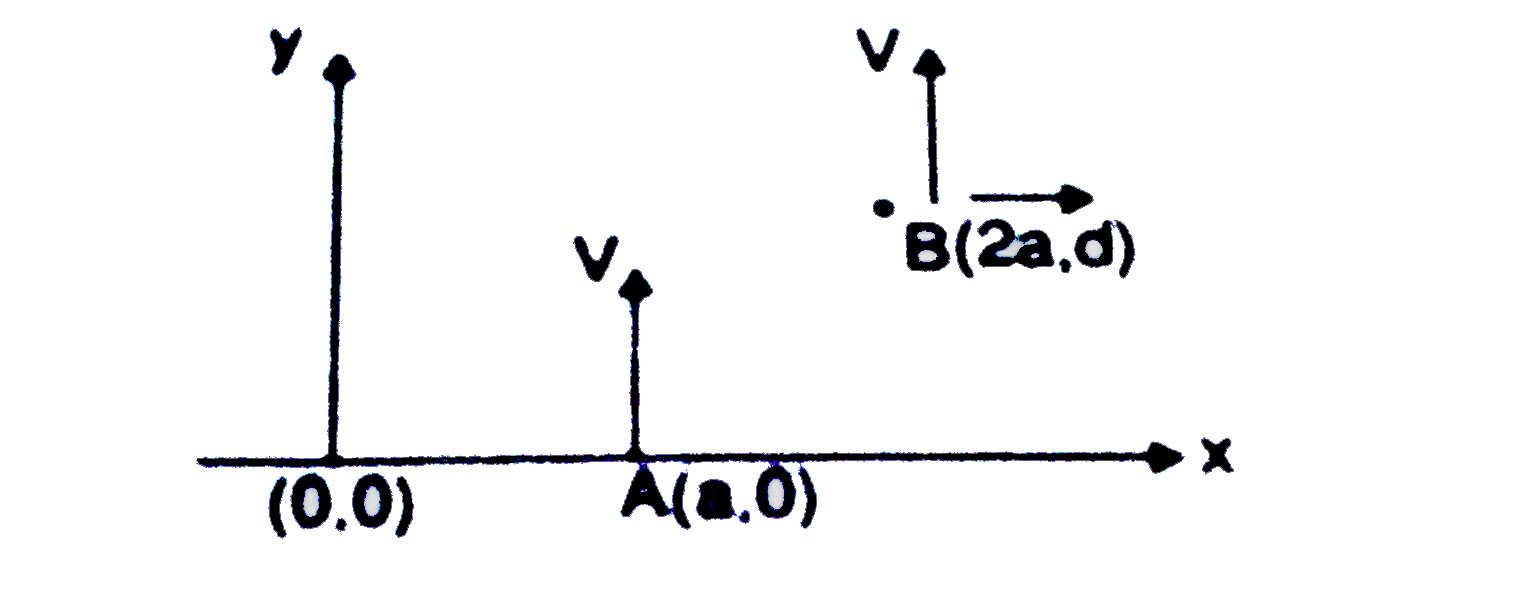 A→E=−2amv2ed2ˆi.BRate of work done by the electric field at B is 4ma2v3d3CRate of work by the electric field at A is zero.DVelocity at B is 2avdˆi+vˆj.
A→E=−2amv2ed2ˆi.BRate of work done by the electric field at B is 4ma2v3d3CRate of work by the electric field at A is zero.DVelocity at B is 2avdˆi+vˆj.
A uniform electric field of strength e exists in a region. An electron (charge -e, mass m) enters a point A with velocity Vˆj. It moves through the electric field & exits at point B. Then :

View SolutionA uniform electric field of strength E exists in region. A electron enters a point A with velocity v as shown. It moves through the electric field and reaches at point B. Velocity particle at B is 2v at 30∘ with x-axis .
Then
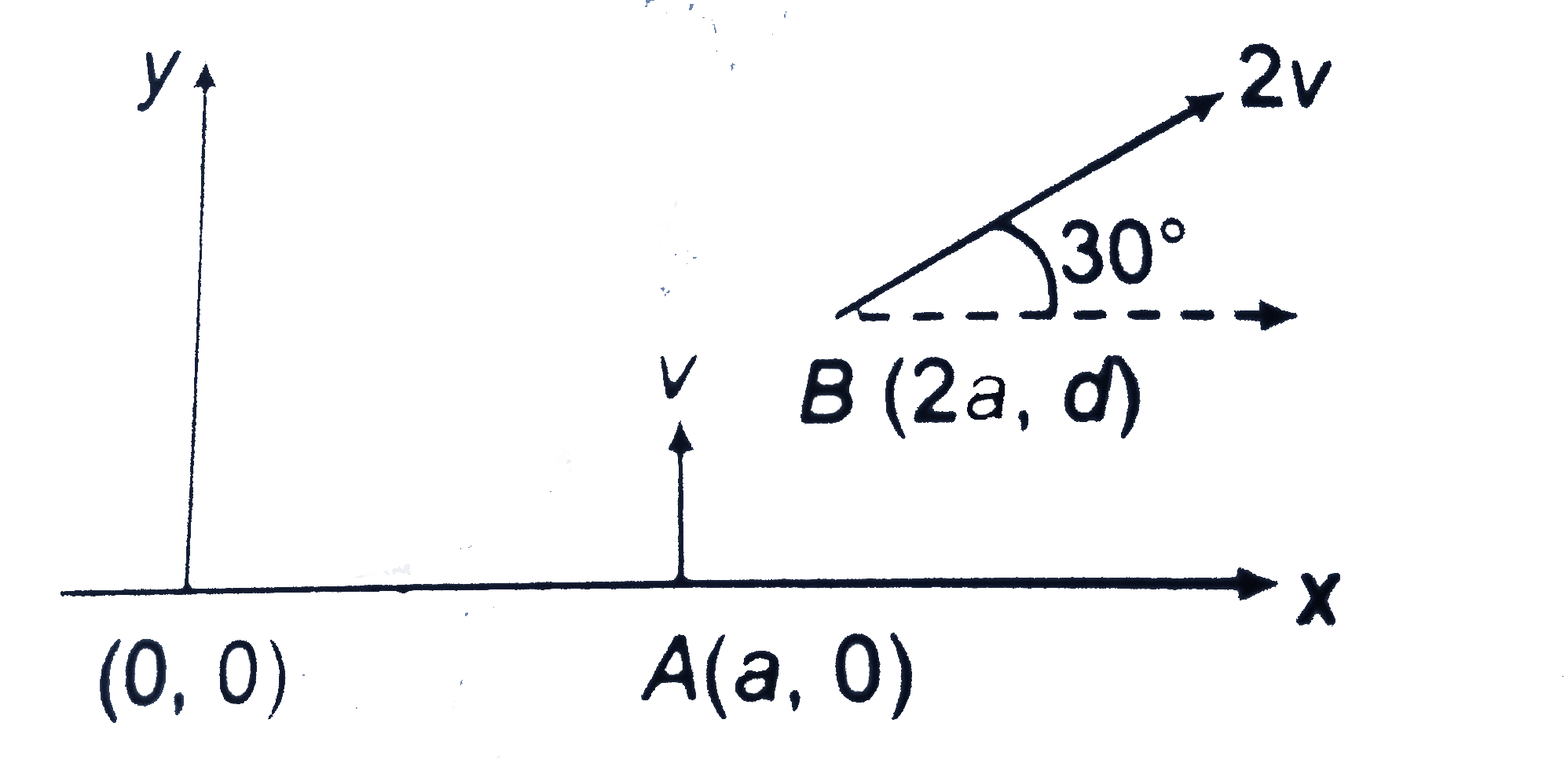
View SolutionA uniform electric field and a uniform magneitc field exist in a region in the same direction An electron is projected with velocity pointed in the same direction the electron will
View SolutionA uniform electric field of strength E exists in region. A electron enters a point A with velocity v as shown. It moves through the electric field and reaches at point B. Velocity particle at B is 2v at 30∘ with x-axis .
Then
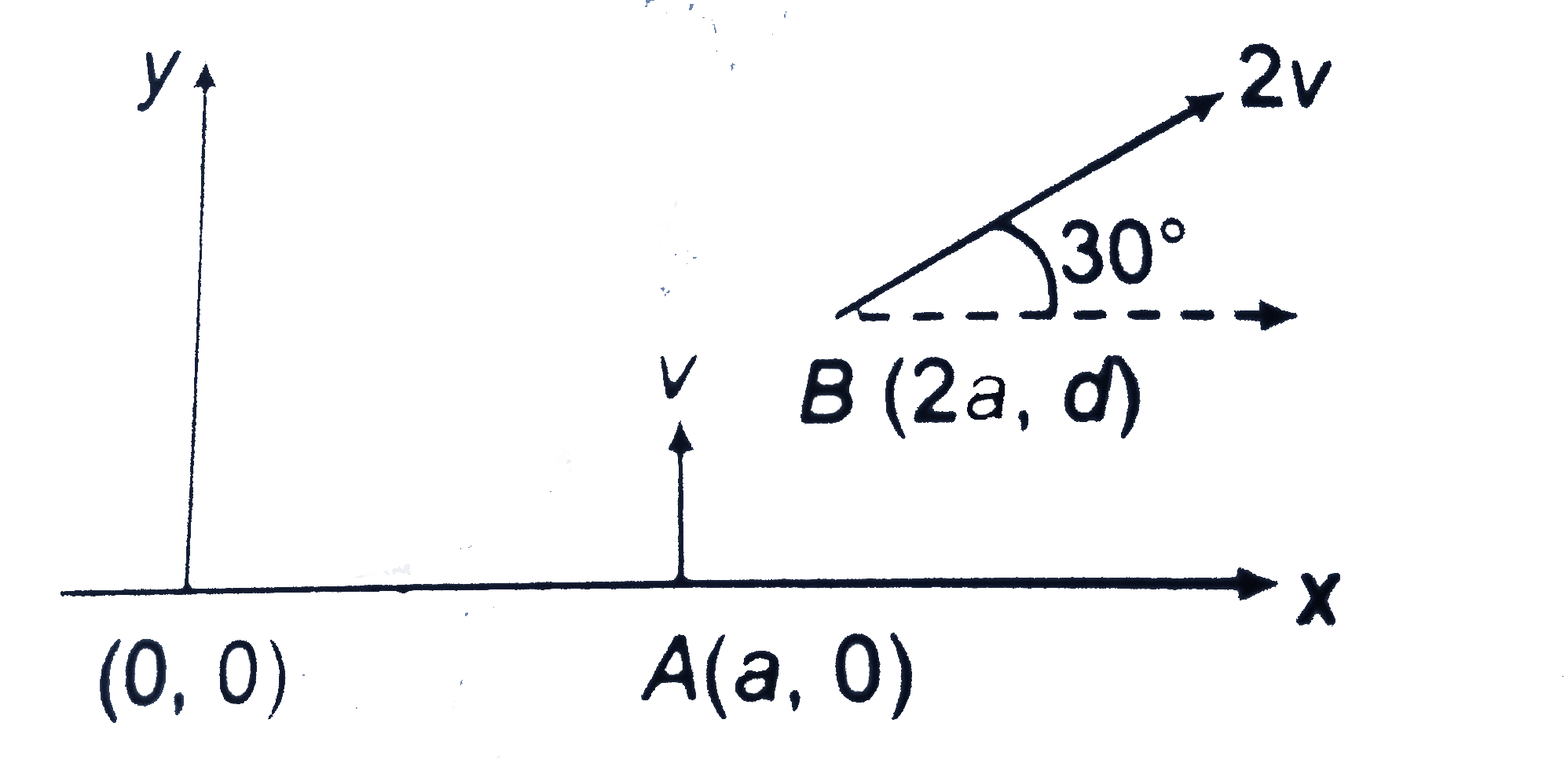
View SolutionA uniform electric field and a uniform magneitc field exist in a region in the same direction An electron is projected with velocity pointed in the same direction the electron will
View Solution
